Friedman检验 (The Friedman Non-parametric Repeated Measures ANOVA Test)——MedCalc软件实现

关键词：MedCalc; 非参数检验; 秩和检验; Friedman检验; 重复测量非参数检验

一、案例介绍

8名受试对象在相同试验条件下分别接受A、B、C 3种不同频率振动的刺激，测量其反应率(%)，问3种频率振动刺激的反应率是否有差别？数据见图1。本案例数据可从“附件下载”处下载。

二、问题分析

本案例的分析目的是判断多组相关数据的差异，首先对3组数据进行正态性检验，若发现不符合正态分布，可以使用Friedman检验(此处的“反应率”是针对个体观察对象所测得的一个反应程度的指标，可以理解为“反应指数”，因此属于连续变量)。Friedman检验可应用于多组配对或相关数据的秩转换非参数检验，但需要满足两个条件：

条件1：观察变量为连续变量或有序分类变量。本研究中反应率为连续变量，该条件满足。

条件2：观察变量具有3个及以上的分组，为配对设计，或各组之间存在相关性。本研究中3组数据均是对同一批研究对象所测量，该条件满足。

三、软件操作及结果解读

(一) 适用条件判断(正态性检验)

1. 软件操作

• 点击“统计”—“分布图”—“正态图”(图2)

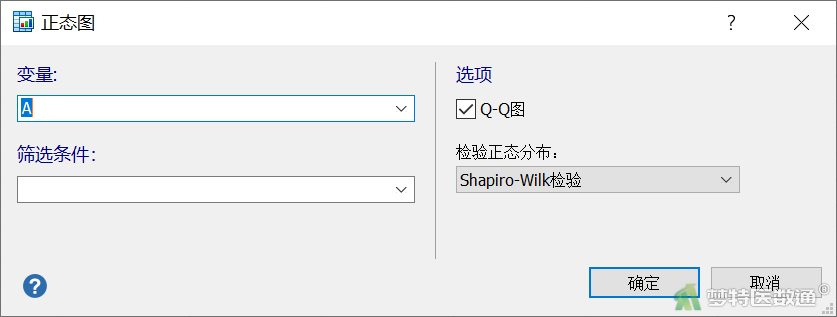
• 在“正态图”主对话框中设置如下参数(图3)，并点击“确定”

①变量：即包含分析资料的变量。本例依次选择“A”/“B”/“C”。

②筛选条件：即设定统计分析的个案子组。本例未选择任何变量。

③选项：勾选“Q-Q图”，可以绘制Q-Q图粗略评价资料是否服从正态分布，本例勾选。“检验正态分布”方法包括“Shapiro-Wilk检验”，常用于3≤n≤50的小样本资料；“Shapiro-Francia检验”，常用于5≤n≤5000的资料；“D’Agostino-Pearson检验”，常用于50≤n≤1000的资料、“Kolmogorov-Smirnov检验”，常用于n>50的资料；“卡方检验”，适用于分箱资料，本例选“Shapiro-Wilk检验”。

• 点击“统计”—“汇总统计”(图4)

• 在“汇总统计”主对话框中设置如下参数(图5)，点击“确定”即可

①变量：即包含分析资料的变量，本例选择“A”/“B”/“C”。

②筛选条件：即设定统计分析的个案子组，本例未选择任何变量。

③选项：“对数变换”当资料为正偏态时可考虑进行对数变换，本例不勾选。“检验正态分布”，依然选择“Shapiro-Wilk检验”。

2. 结果解读

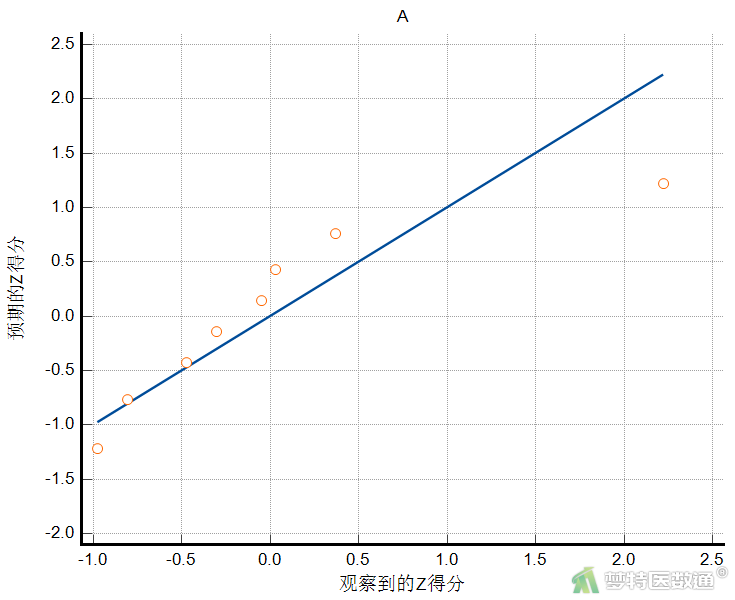
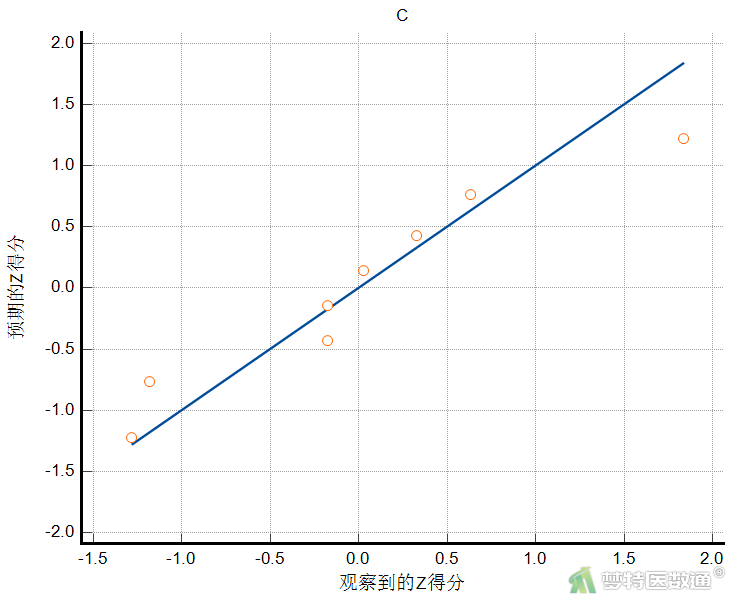
由图6-1至图6-3可知，3组散点偏离对角线较远，尤其是A、B两组数据，提示3组数据不服从正态分布。

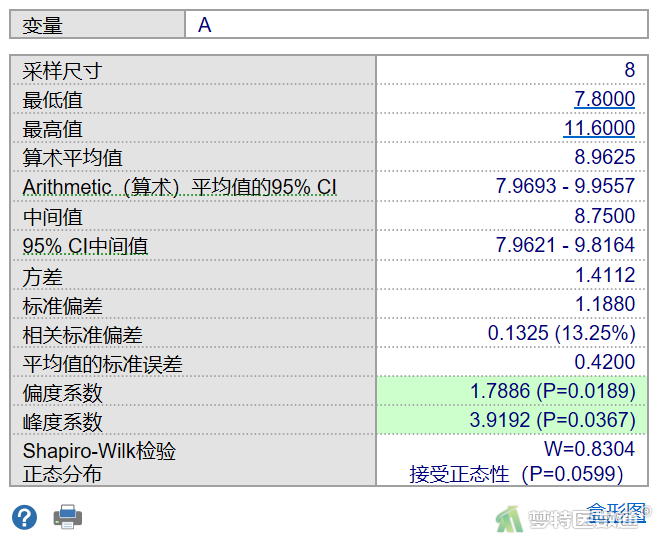
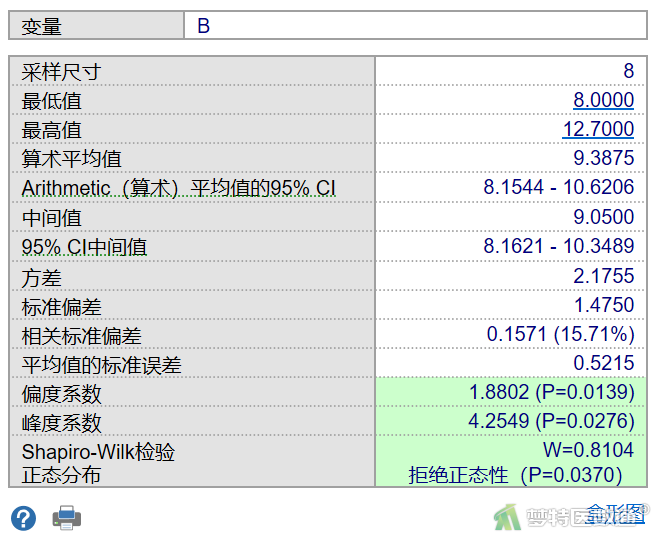
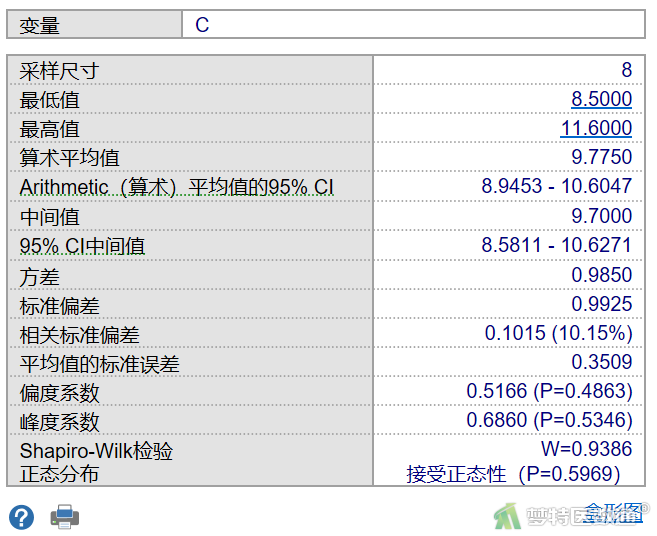
由图7-1至图7-3结果可知，A、B、C三组的正态性检验P=0.0599、0.0370、0.5969，前两组P值均<0.1，提示A、B两组数据不服从正态分布。因此，本案例应使用Friedman检验比较3组反应率的差异。关于正态性检验的注意事项详见(医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现)。

(二) 整体检验

1. 软件操作

• 点击“统计”—“方差分析”—“弗里德曼检验”(图8)

• 在“Friedman检验”主对话框中设置如下参数(图9)，并点击确定

①变量：即包含相关样本的变量。本例选择“A”“B”“C”。

②筛选条件：即设定统计分析的个案子组。本例未选择任何变量。

③选项-显著性水平：即事后检验的期望显著性水平，若检验结果的P值小于该水平，则使用Conover法进行事后检验。本例选“0.05”。

2. 结果解读

(1) 统计描述

图10“描述统计”提供了研究案例的“n (样本量)”、“最低”、“第25个百分位数”、“中间值”、“第75个百分位数”和“最高”值。可知，受试者对A频率振动的反应率为8.75% (P₂₅~P₇₅：8.20%~9.20%)；对B频率振动的反应率为9.05% (P₂₅~P₇₅：8.45%~9.70%)；对C频率振动的反应率为9.70% (P₂₅~P₇₅：9.10%~10.25%)。

(2) 统计推断

图11显示了Friedman检验的结果，可知χ²=6.0233, P=0.01296< 0.05，差异有统计学意义。即3种频率振动刺激的反应率总体比较差异不全相同(P < 0.05) (即至少存在两组不相同)。

(三) 事后检验

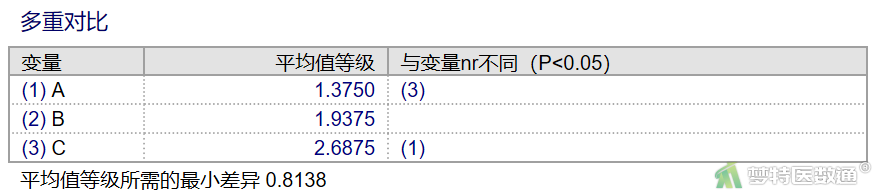
图12使用Conover法进一步两两比较结果显示，3种频率下反应率的平均秩分别为1.3750、1.9375和2.6875，当两个频率平均秩之差超过0.8138时，表明两个频率之间的刺激反应率差异有统计学意义。本例频率A和频率C的刺激反应率差异有统计学意义，频率A和频率B的刺激反应率差异无统计学意义，频率B和频率C的刺激反应率差异无统计学意义。

点击图12右下角“多重变量图表”，在“多重变量图表”对话框按照图13设置各参数，点击“确定”即可。

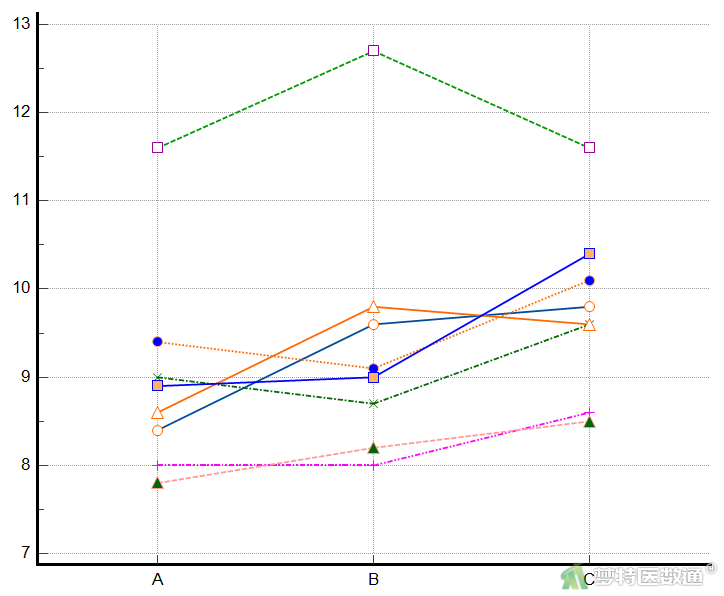
图14的多重变量图详细呈现了3种频率刺激下各研究对象的反应率情况。

四、结论

本案例欲比较在A、B、C 3种不同频率振动的刺激下受试者的反应率(%)是否存在差异。通过绘制Q-Q图和Shapiro-Wilk检验，提示数据不服从正态分布，故采用Friedman检验对数据进行分析。

结果显示，受试者对A、B、C 3种不同频率振动的刺激反应率分别为8.75% (P₂₅~P₇₅：8.20%~9.20%)、9.05% (P₂₅~P₇₅：8.45%~9.70%)、9.70% (P₂₅~P₇₅：9.10%~10.25%)，差异有统计学意义(χ²=6.0233, P=0.01296)。进一步两两比较显示，频率A和频率C的刺激反应率差异有统计学意义，频率A和频率B的刺激反应率差异无统计学意义，频率B和频率C的刺激反应率差异无统计学意义。