在前面文章中介绍了配对样本Wilcoxon符号秩检验(Paired Samples Wilcoxon Signed Rank Test)——理论介绍,本文将实例演示在MedCalc软件中实现配对样本Wilcoxon符号秩检验的操作步骤。
关键词:MedCalc; 非参数检验; 秩和检验; 配对样本Wilcoxon符号秩检验; 配对秩和检验
一、案例介绍
对12份血清分别用原方法(检测时间15分钟)和新方法(检测时间10分钟)测谷草转氨酶,问两种方法所得结果是否有差别?变量“Old”和“New”分别表示用原方法和新方法测得的谷草转氨酶含量,“change”为两方法测得谷草转氨酶含量的差值。部分数据见图1。本案例数据可从“附件下载”处下载。

二、问题分析
本案例的分析目的是比较对同一组样品使用两种方法检测的结果是否有差异,即判断用新方法与原方法检测血清谷草转氨酶含量是否存在差异,属于配对设计定量资料比较的范畴。对于配对设计的连续性变量比较,可以选用配对t检验或Wilcoxon符号秩检验。配对t检验适用于两组差值近似服从正态分布的数据。当不满足该条件时,可选择Wilcoxon符号秩检验。首先,对新方法与原方法检测血清谷草转氨酶含量的差值进行正态性检验,若发现差值不服从正态分布,则应选用配对样本Wilcoxon符号秩检验。使用Wilcoxon 符号秩检验时,需要满足3个条件:
条件1:观察变量是连续变量或有序分类变量。本研究中的谷草转氨酶水平为连续变量,该条件满足。
条件2:观察变量可分为2组。本研究中分为原方法和新方法,该条件满足。
条件3:观察变量的数据结构为配对形式。本研究中数据属于同一组样品自身配对的形式,该条件满足。
三、软件操作及结果解读
(一) 适用条件判断
1. 条件1判断(正态性检验)
(1) 软件操作
选择“统计”—“分布图”—“正态图”(图2)。
在“正态图”对话框(图3),“变量”下选择change,“选项”中勾选“Q-Q图”,“检验正态分布”下选择“Shapiro-Wilk检验 (夏皮罗-威尔克正态性检验,S-W检验)”。

选择“统计”—“汇总统计”(图4),打开“汇总统计”对话框(图5),“变量”下选择change,“检验正态分布”下选择“Shapiro-Wilk检验 (夏皮罗-威尔克正态性检验,S-W检验)”。

(2) 结果解读
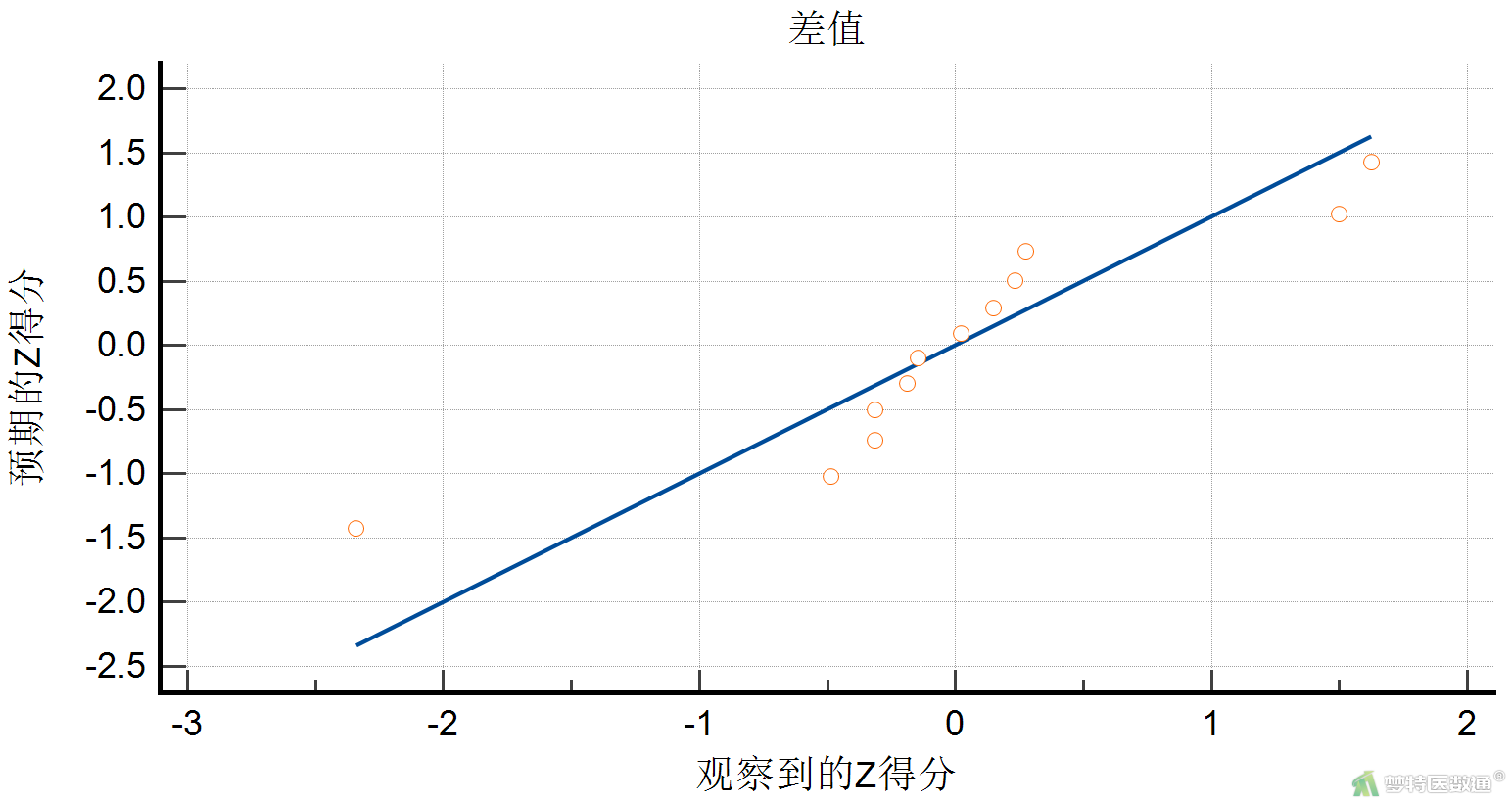
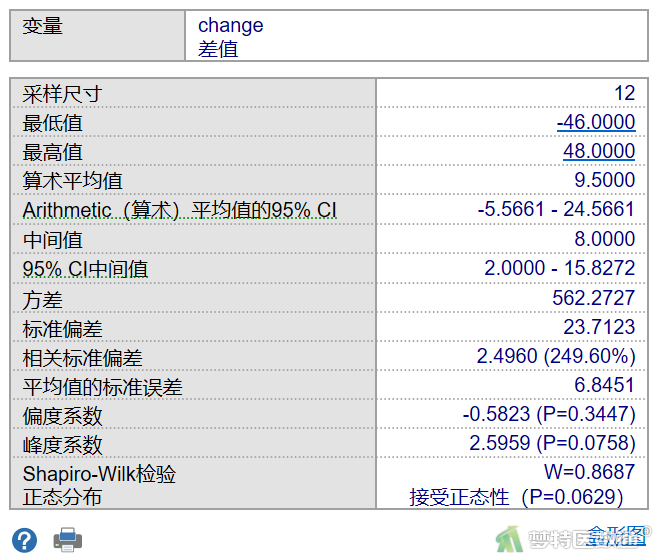
两种方法检测血清谷草转氨酶含量差值的Q-Q图(图6),两组散点偏离对角线较远,提示该组数据不服从正态分布。Shapiro-Wilk检验 (夏皮罗-威尔克正态性,S-W检验)结果(图7),W=0.8687,P=0.0629<0.1,也提示数据不服从正态分布。关于正态性检验的更多内容请阅读(医学统计学核心概念及重要假设检验的软件实现(2/4) ——正态性假设检验的SPSS实现)。
(二) 统计描述及推断
1. 软件操作
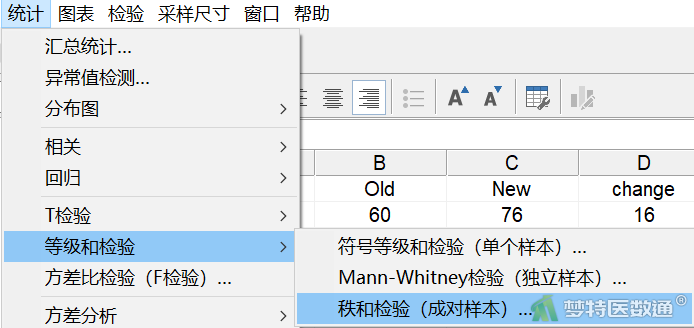
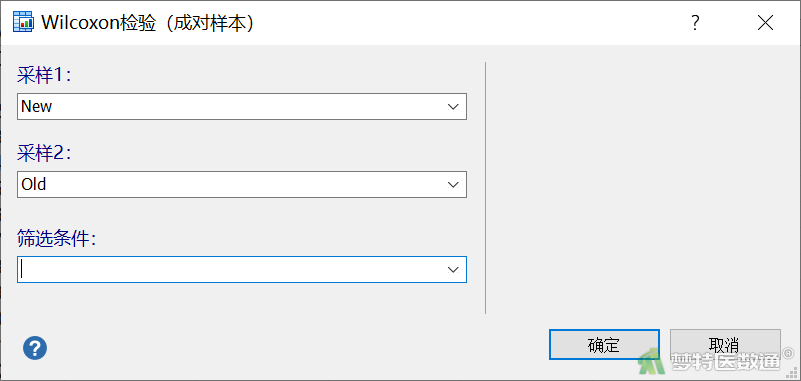
选择“统计”—“等级和检验”—“秩和检验(成对样本)” (图8),打开“Wilcoxon检验(成对样本)”对话框(图9),“采样1”下选择New,“采样2”下选择Old。
2. 结果解读
(1) 统计描述
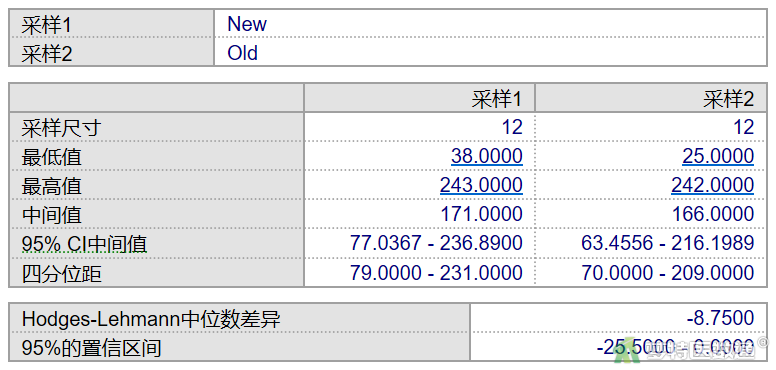
两组变量的统计描述结果(图10)显示,使用原方法和新方法的两组“个案数”均为12,新方法测得的血清谷草转氨酶含量中位数为171.00,四分位间距为79.00~ 231.00;原方法测得的血清谷草转氨酶含量中位数为166.00,四分位间距为70.00~ 209.00。从中位数看两组可能存在差异,但还需依据统计学检验的结果进行判断。
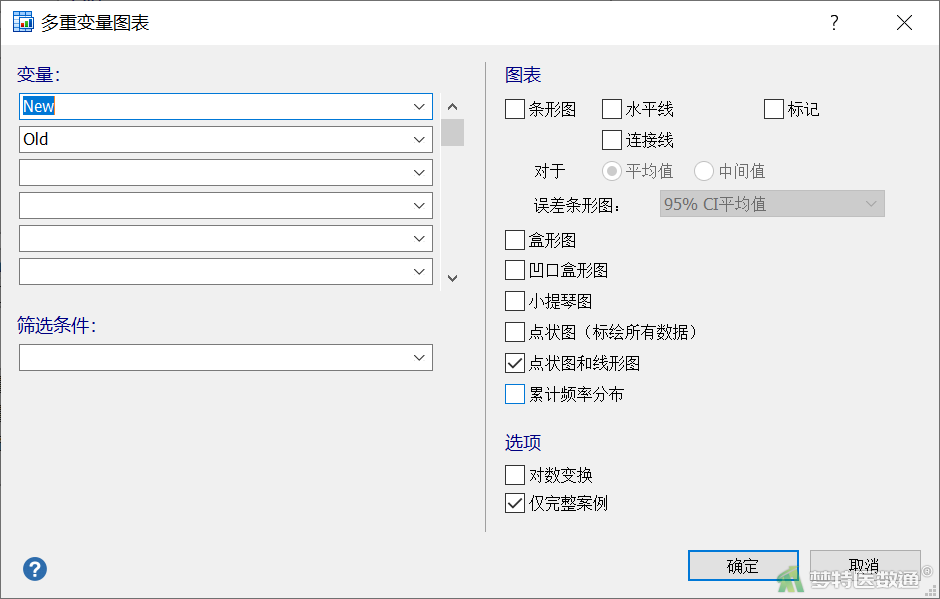
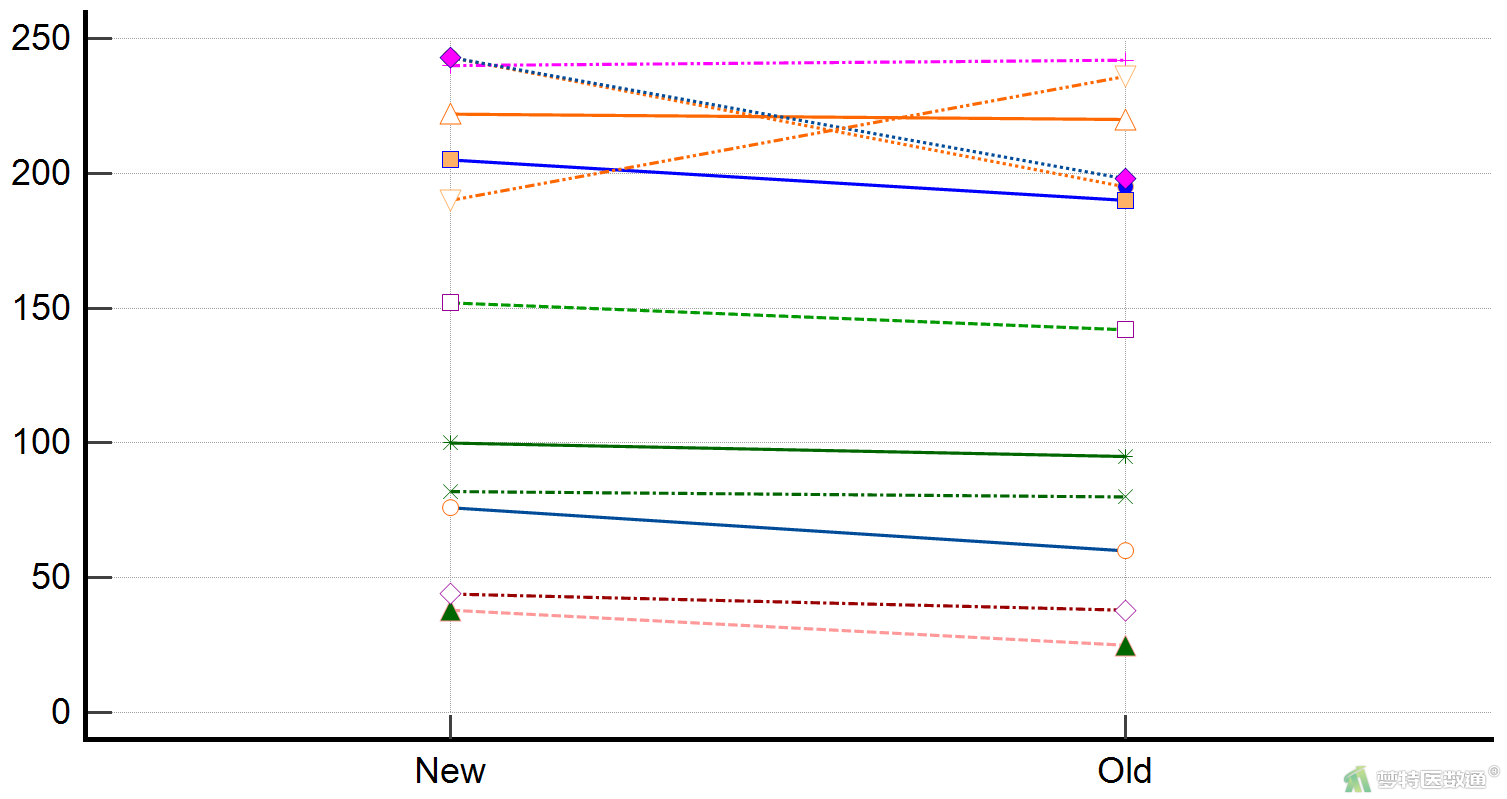
点击数据分析页面右下角的“点线图”,可出现“多重变量图表”对话框(图11),点击“确定”可得到两组数据比较的点线图(图12)。
(2) 统计推断
配对样本Wilcoxon符号秩检验的结果见图13,基于负秩计算得到的统计量Z =2.040, P= 0.041<0.05,表明两组数据中位数差值与0的差异具有统计学意义,即通过原方法和新方法检测的血清谷草转氨酶含量的中位数不同,可以认为两种方法检测的结果不同。

四、结论
本研究欲比较新方法与原方法检测血清谷草转氨酶含量是否存在差异,对新方法与原方法检测数值的差值进行正态性检验发现差值不符合正态分布,故选用配对样本Wilcoxon符号秩检验进行分析。
结果显示,原方法检测血清谷草转氨酶的含量为166.00 (70.00~ 209.00) nmol/SL;新方法检测血清谷草转氨酶的含量为171.00 (79.00~ 231.00) nmol/SL,两种方法检测结果差值的中位数为8.75 (95%CI -25.50~0.00) nmol/SL,差异有统计学意义(Z =2.040, P= 0.041),可以认为两种方法检测的结果不同。
五、知识小贴士
- 两组配对设计在临床研究中经常使用,针对连续性变量,主要有配对样本t检验和配对样本Wilcoxon符号秩检验两种分析方法。配对样本t检验的限制条件较多(详见配对样本t检验(Paired Samples t-test)——MedCalc软件实现),但统计学效能更高;Wilcoxon符号秩检验的限制条件较少,但统计效能相较于配对样本t检验低。对于定量资料,若不满足正态性和方差齐性条件,这时小样本资料应选择秩转换的非参数检验更为恰当。
- 尽管通常认为参数检验的统计学效能优于非参数检验,但这指的是在满足参数检验的适用条件前提下,当不满足参数检验的适用条件时强行使用参数检验会降低其统计学效能,甚至会得出错误的结果。