对于许多统计学检验,都要求连续性变量所对应的总体服从正态分布。但由于总体未知或未能获取,所以实际数据分析过程中是通过考察样本的正态分布情况来判断总体正态性。如单样本t检验要求样本服从(近似)正态分布,独立样本t检验要求两组样本均服从(近似)正态分布,配对样本t检验要求两组差值服从(近似)正态分布。本篇文章便将通过实例演示正态性检验在SPSS软件中的实现及注意事项。
关键词:正态性检验; 正态分布; SPSS; Kolmogorov-Smirnov检验; Shapiro-Wilk检验; Q-Q图; P-P图
一、案例数据
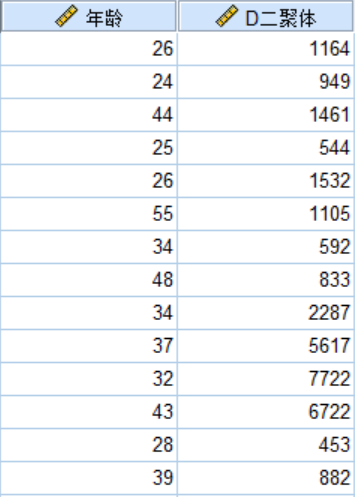
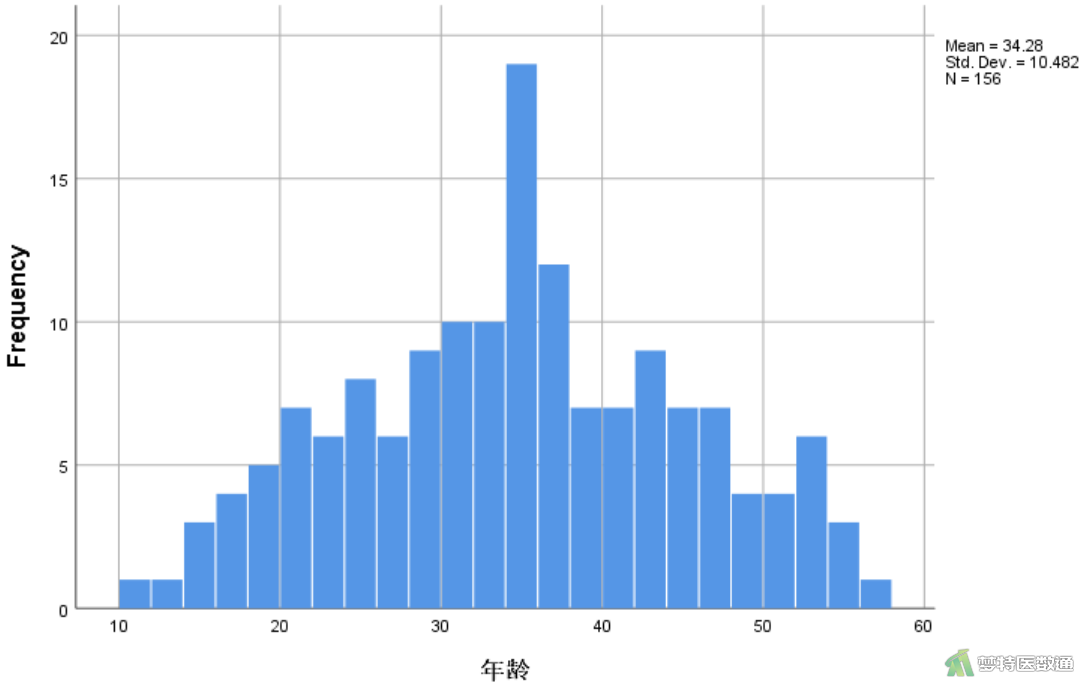
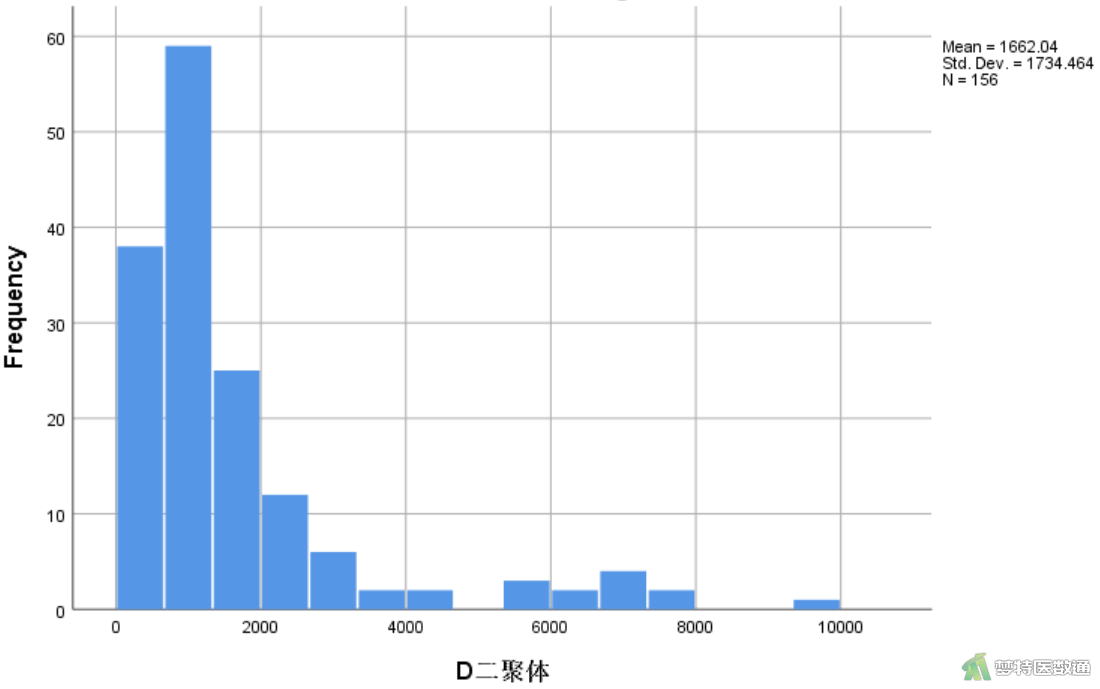
调查了156名研究对象的年龄(岁)和血液中D-二聚体浓度(μg/L),试分析两个指标是否服从正态分布,部分数据见图1。
二、软件实现及结果解读
(一) 图形法
1. 直方图
直方图可以直观地显示数据的分布形式。
(1) 软件操作
①选择“Analyze(分析)”—“Descriptive Statistics(描述统计)”—“Explore(探索)”(图2)。
②在“Explore(探索)”子对话框中,将“年龄”和“D二聚体”选入“Dependent List(因变量列表)”(图3),然后点击“Plots(图)”。
③在“Plots(图)”子对话框中勾选“Histogram(直方图)”(图4),点击“Continue(继续)”,然后点击OK。
(2) 结果解读
由图5和图6可知,年龄的直方图基本呈现正态分布,D-二聚体的直方图呈现明显的正偏态分布。
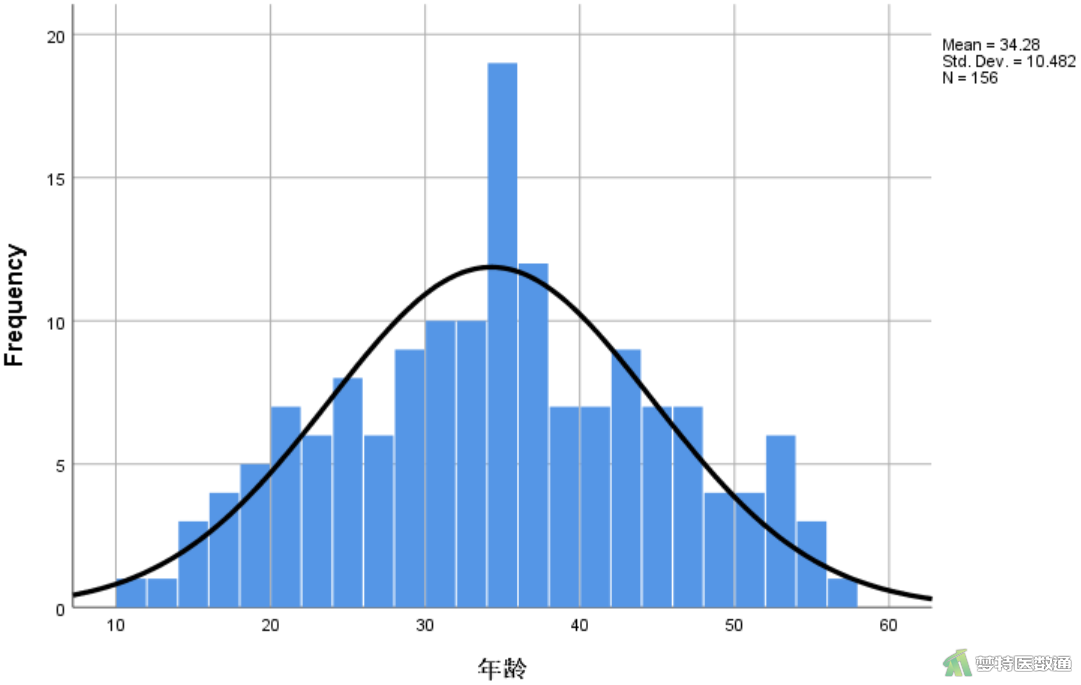
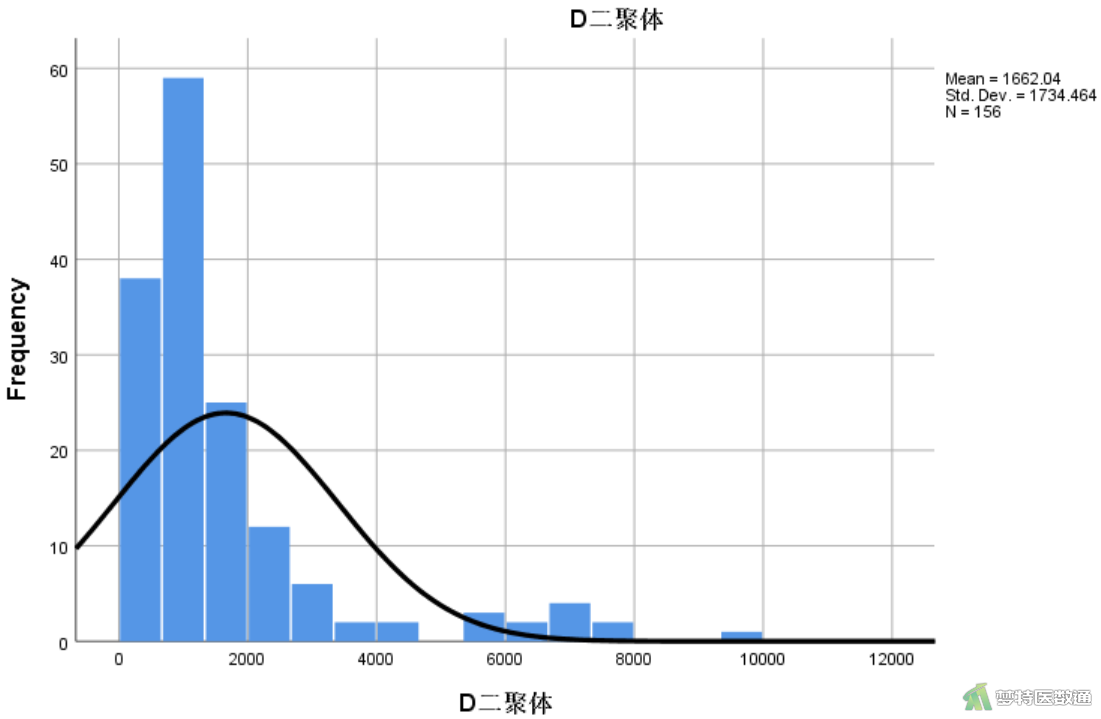
也可通过以下步骤绘制直方图:“Analyze(分析)”—“Descriptive Statistics(描述统计)”—“Frequencies(频率)”,在“Charts(图表) ”中勾选“Histograms(直方图)”和“Show normal curve on histogram(在直方图中显示正态曲线)”, 点击“Continue(继续)”,然后点击OK。结果如图7和图8所示。但此处只能输出整体数据的图形,若要实现分组输出(如独立样本t检验时),则需要先将数据按组别进行拆分。
2. Q-Q图
Q-Q图又称分位数图(quantile-quantile plot),是以实际或观察的分位数(X)对被检验分布的理论或期望分位数(Y)作图。如果所分析的数据服从正态分布,则在Q-Q图上的数据点应分布在从左下到右上的直线附近。
(1) 软件操作
实现Q-Q图既可以从“Analyze(分析)”—“Descriptive Statistics(描述统计)”—“Explore(探索)” 模块中实现,即在“Plots(图)”中勾选“Normality plots with tests(含检验的正态图)”(图9),也可以从“Descriptive Statistics(描述统计)”—“Q-Q plots (Q-Q图)”专门模块实现(图10)。但是此处需要注意的是,“Explore(探索)”模块通过“Factor List(因子列表)”可以直接实现不同组别结果的单独输出,而“Q-Q plots (Q-Q图)”只能输出整体数据的图形,若要实现分组输出,则需要先将数据按组别进行拆分。
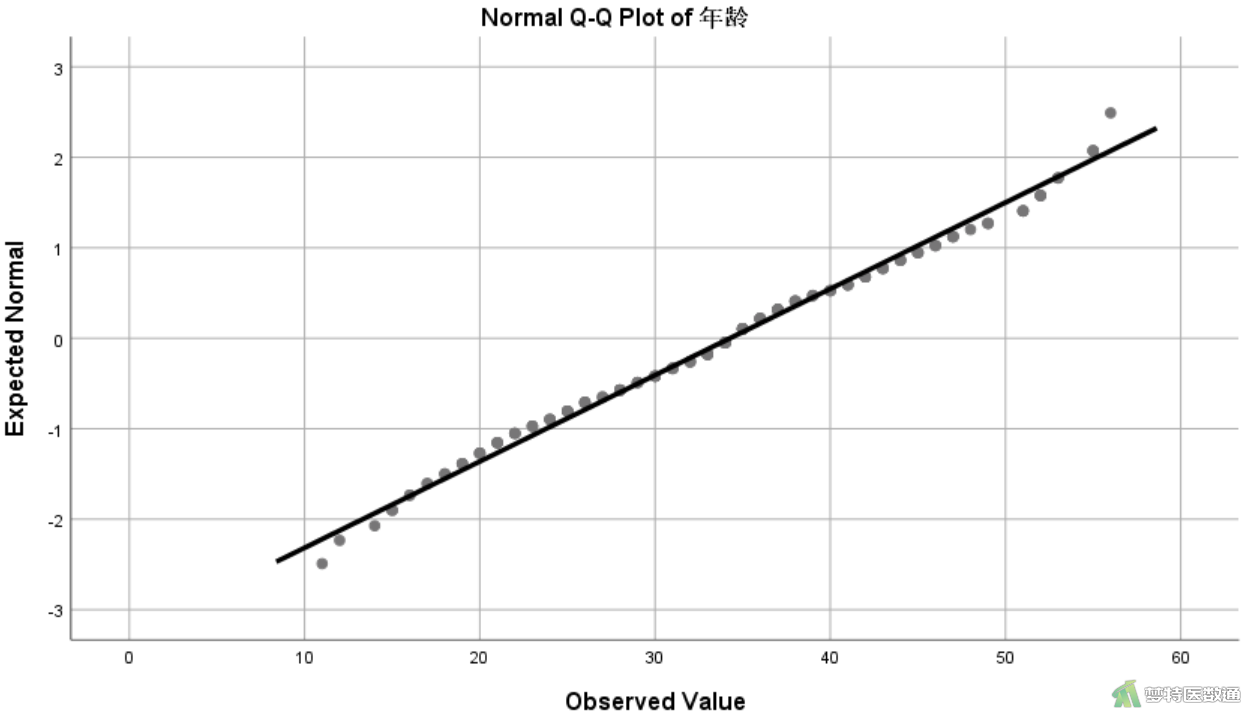
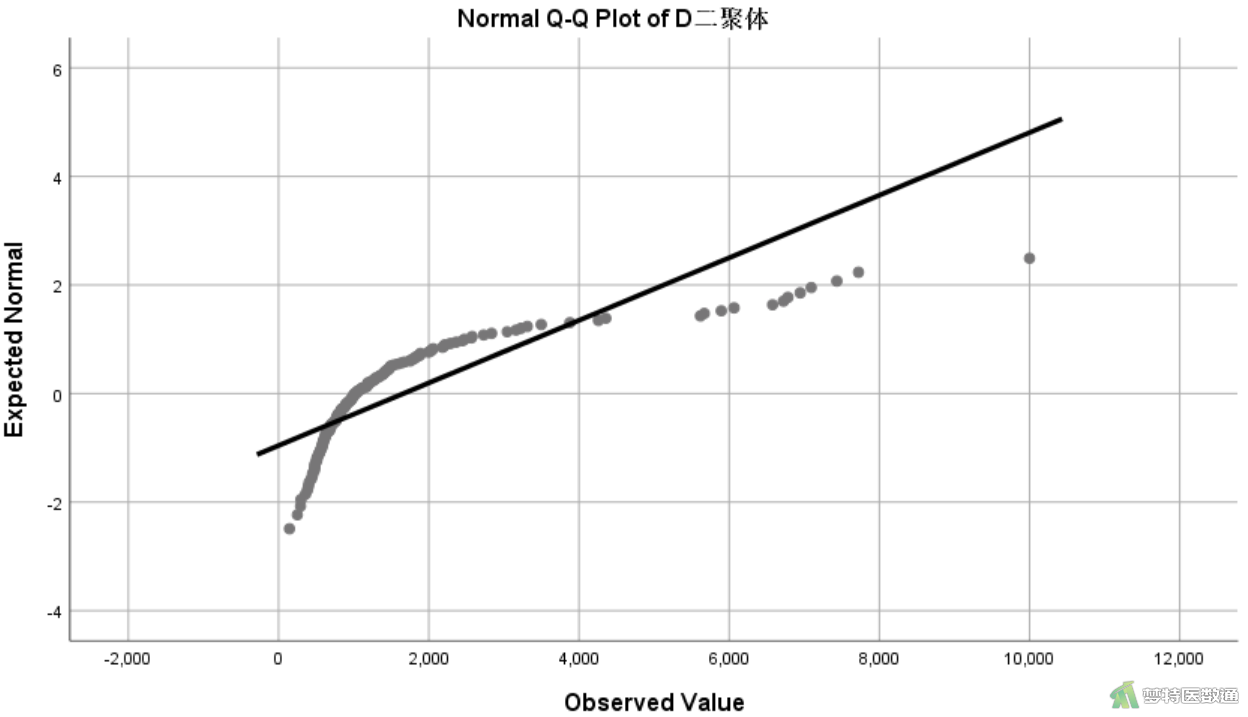
(2) 结果解读
由图11和图12可见年龄的数据点均围绕着斜线分布,呈现正态分布;而D-二聚体的数据点偏离斜线较远,呈现明显的偏态分布。
3. P-P图
P-P图又称概率图(probability- probability plot),是以实际或观察的累积频率(X)对被检验分布的理论或期望分位数(Y)作图。如果所分析的数据服从正态分布,则在P-P图上的数据点应分布在从左下到右上的直线附近。
(1) 软件操作
选择“Analyze(分析)”—“Descriptive Statistics(描述统计)”—“P-P plots (P-P图)”,在“P-P plots (P-P图)”子对话框中将变量“年龄”和“D二聚体”选入“Variables(变量)”框,在“Test Distribution(分布检验)”中选择“Normal(正态性)”,点击OK(图13)。
(2) 结果解读
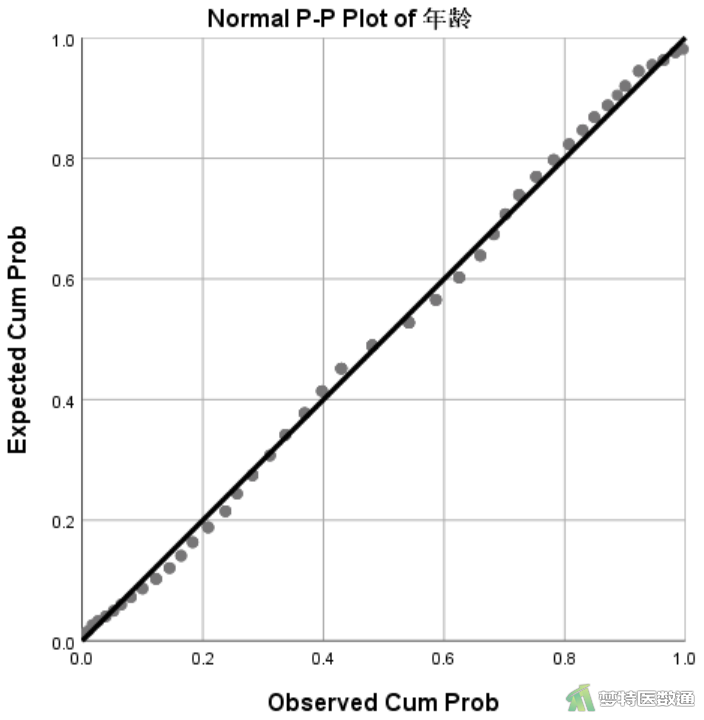
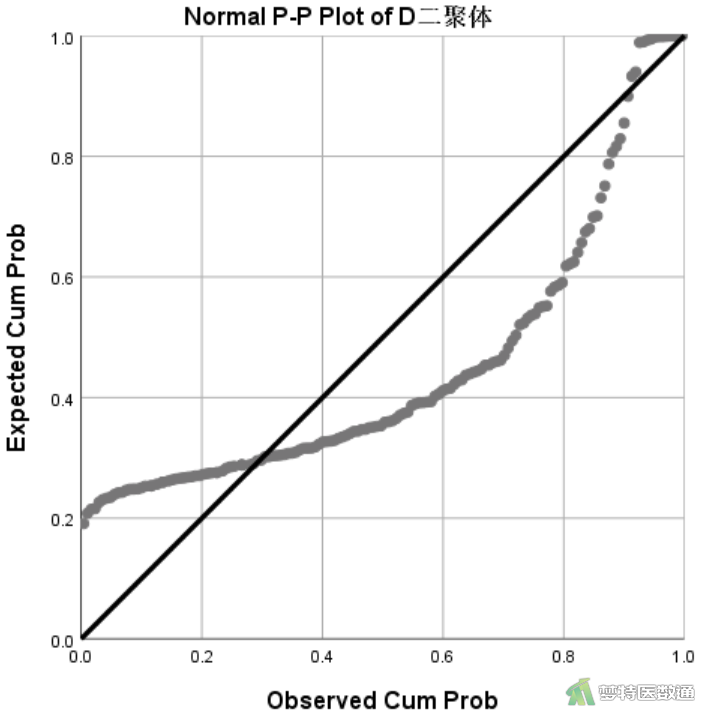
由图14和图15可见年龄的数据点均围绕着斜线分布,呈现正态分布;而D-二聚体的数据点偏离斜线较远,呈现明显的偏态分布。
(二) K-S检验和S-W检验法
1. 软件操作
选择“Analyze(分析)”—“Descriptive Statistics(描述统计)”—“Explore(探索)”,在“Plots(图)”子对话框中勾选“Normality plots with tests(含检验的正态图)”(图9),点击“Continue(继续)”,然后点击OK。
2. 结果解读
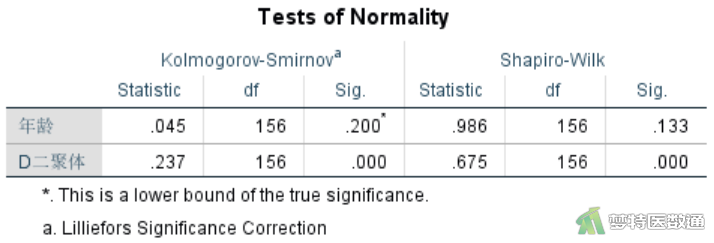
Kolmogorov-Smirnov检验(K-S检验)适用于大样本(SPSS建议n≥5000时使用),Shapiro-Wilk检验(S-W检验)适用于小样本。本案例样本量远小于5000,建议使用S-W检验结果。从图16“Tests of Normality(正态性检验)”结果可知,取检验水准α=0.1时,年龄服从正态分布(P=0.133),D-二聚体不服从正态分布(P<0.001)。
(三) 偏度和峰度系数检验法
理论上,总体偏度系数γ1=0为对称,γ1>0为正偏态,γ1<0为负偏态;峰度系数γ2=0为正态峰,γ2>0为尖峤峰,γ2<0为平阔峰。对其样本的偏度系数g1和峰度系数g2可以进行u检验,在α=0.1的检验水准下,若|u|<1.64,则可认为数据近似服从正态分布。
其中:
ug1=g1/σ1 σ1为偏度系数的标准误
ug2=g2/σ2 σ2为峰度系数的标准误
1. 软件操作
①选择“Analyze(分析)”—“Descriptive Statistics(描述统计)”—“Descriptives(描述)”, 将“年龄”和“D二聚体”选入“Variable(变量)”(图17)。
②在“Options(选项)”子对话框中勾选“Kurtosis(峰度)”和“Skewness(偏度)”(图18),点击“Continue(继续)”,然后点击OK。
2. 结果解读
由图19“Descriptive Statistics(统计描述)”结果可计算年龄的检验统计量为:
偏度系数检验统计量ug1=g1/σ1=0.018/0.194=0.093,|ug1|<1.64
峰度系数检验统计量ug2=g2/σ2=-0.622/0.386=-1.611,|ug2|<1.64
表明年龄服从正态分布。
D-二聚体的检验统计量为:
偏度系数检验统计量ug1=g1/σ1=2.455/0.194=12.655,|ug1|>1.64
峰度系数检验统计量ug2=g2/σ2=6.074/0.386=15.736,|ug2|>1.64
表明D-二聚体不服从正态分布。

(四) 描述法
1. 软件操作
选择“Analyze(分析)”—“Descriptive Statistics(描述统计)”—“Explore(探索)”,在“Statistics(统计)”子对话框中勾选“Descriptives(描述)”(图20),点击“Continue(继续)”,然后点击OK。
2. 结果解读
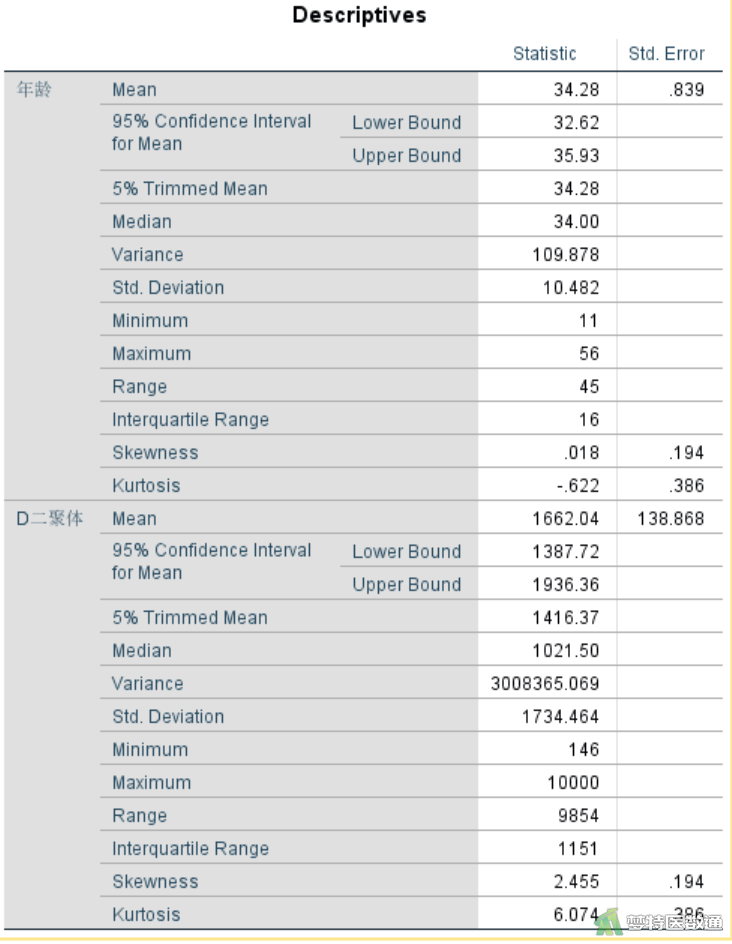
(1) 比较均数和标准差:如果标准差过大(>1/2均数),暗示数据不服从正态分布。图21“Descriptive(结果描述)”中年龄的均数为34.28,标准差为10.48,标准差<1/2均数,提示数据服从正态分布或近似正态分布。D-二聚体的均数为1662.04,标准差为1734.46,标准差已经超过了均数,提示数据不服从正态分布。
(2) 比较均数和中位数:如果均数和中位数相差太远,暗示数据不服从正态分布。本案例中年龄的均数为34.28,中位数为34.00,非常接近,提示数据服从正态分布或近似正态分布。D-二聚体的均数为1662.04,中位数为1021.50,差距很大,提示数据不服从正态分布。
三、正态性检验的注意事项
(一) 非绝对化
正态性检验只是基于统计学原理进行的一种假设检验(或猜想),本身就带有不确定性,真正的总体分布类型多数时候是未知的,因此也并没有一种绝对权威的方法能判断一个样本来自于什么样的总体,所以不必对检验结果给予太绝对化的结论。
(二) 结合专业
是否符合正态分布,还需要结合专业知识进行综合判定,大多数医学数据都不符合正态分布,如血脂、血糖、肝酶、肿瘤标志物等以及开口资料和量纲是指数级的资料。
(三) 结合样本量
由于参数检验具有更好的检验效能,因此经验数据,特别是样本小的数据,其正态性检验不应太严格。但对于样本量过小的数据,最好采用非参数检验。大样本数据一般可放宽正态性检验的标准,但极端偏态分布资料或者专业知识认为不符合正态分布的资料除外。
(四) 各种判断方法的选择
表面上看,K-S、S-W等假设检验法应该是考察数据正态性最精确的方式,但事实并非如此。假设检验受样本量的影响较大,样本偏低时不够敏感,样本较大时又会过于敏感;而描述法的主观性较大,因此建议首选图形分析。统计检验法对于数据的要求最为严格,而实际数据由于样本不足等原因,即使数据总体正态但统计检验出来也显示非正态,因而一般情况下使用图示法相对较多,只要正态性情况在一定可接受范围内即可。
(五) 具体统计学方法的正态性检验要求
1. 单样本t检验,考察原始数据的正态性;两独立样本t检验,考察每组原始数据的正态性;配对样本t检验,考察差值的正态性。
2. 单因素方差分析时,使用原始数据分别检验每组的正态性。
3. 两因素或多因素方差分析时,有两种选择来测试正态性:如果每个X值(每组)确实有很多Y值,而实际上只有几个组(比如,4个或更少),那么可使用原始数据检查每个组的正态性。如果有很多组(2×2×3方差分析有12组),或者如果每个组的观察数很少,那么可使用残差检查整体(不是分组)的正态性。
4. 单因素重复测量方差分析时,使用原始数据分别检验每组的正态性。
5. 两因素或多因素重复测量方差分析时,使用原始数据分别检验每组每个重复测量时的正态性。
6. 如果模型中有一个连续的协变量(如协方差分析),只能使用残差检验正态性。
7. Pearson相关性分析时,要求双变量均服从正态分布。
8. 线性回归分析时,要求残差服从正态分布。
9. t检验、方差分析等分析方法对数据的分布具有一定的耐受性,如果不是严重偏态分布,一般情况下,结果仍然稳健。
(六) 检验水准
正态性检验的重要目的是减少II型错误,因此若使用假设检验法判断正态性,其检验水准一般取α=0.1或0.2,甚至更高。
(七) SPSS模块分析注意事项
SPSS中“Explore(探索)”模块里出现的“Kolmogorov-Smirnov”检验是经过Lilliefors改进和校正过的结果,可用于一般性的正态性检验;而在“Nonparametric Tests(非参数检验)”模块中的“Kolmogorov-Smirnov”检验是没有经过改进的,只能做标准正态性检验,检验效率低下,易受样本量和异常值等因素的影响,较少使用。