加速失效时间模型(Accelerated Failure Time Model)——R软件实现

关键词：R软件; 生存分析; Cox回归; 加速失效时间模型; AFT模型

在使用Cox等比例风险回归模型进行预后的影响因素分析时，待分析的影响因素(协变量)需满足等比例风险假设(proportional hazards，PH)，即协变量对生存率的影响不随时间的改变而改变。只有该条件得到满足，Cox回归模型的结果才有效。

当不满足该条件的协变量较多时，可以采用参数回归模型替代Cox等比例风险回归模型进行分析，如加速失效时间(Accelerated Failure Time，AFT)模型。AFT模型直接对生存时间建模，因而无需满足PH假设。

一、案例介绍

本案例使用Cox比例风险回归模型(Cox Proportional Hazard Regression Model)——R软件实现一文案例。某肿瘤研究所收集了200例肺癌患者的生存数据：包括生存状态 (status，1=删失，2=死亡)、生存时间 (time，天)；性别 (sex，1=男，2=女)、年龄 (age，岁)和卡氏评分 (ph.karno)，部分数据见图1。现欲探究患者的性别、年龄、卡氏评分与生存结局的关系。案例可从“附件下载”处下载。

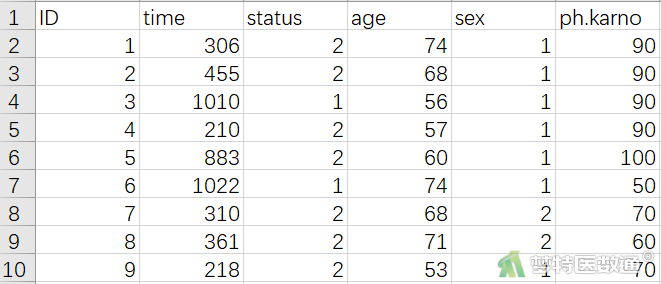
二、问题分析

本案例的目的是探究肺癌患者的性别、年龄和卡氏评分与生存结局的关系，通常可采用Cox比例风险回归模型进行分析，所需要满足的相应条件，见Cox比例风险回归模型(Cox Proportional Hazard Regression Model)——R软件实现。当有协变量不满足等比例风险假设时，则可考虑使用AFT模型。

三、软件操作及结果解读

(一) 导入数据

mydata = read.csv("加速失效时间模型.csv", header = T) #导入CSV数据
View(mydata) #查看数据
str(mydata) #显示数据集内部结构

#添加标签#
attr(mydata$age, "label") = "年龄"
mydata$sex <- factor(mydata$sex, levels = c(1, 2), labels = c("男性", "女性"))
attr(mydata$sex, "label") = "性别"
attr(mydata$ph.karno, "label") = "卡氏评分"

结果见图2。

(二) 检验PH假设

1. 软件操作

构建多因素Cox回归模型并检验PH假设。

library(survival)
fit <- coxph(Surv(time, status) ~ factor(sex) + age + ph.karno, data = mydata) 
summary(fit)
ph.test <- cox.zph(fit)
ph.test

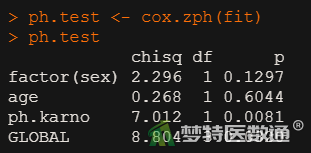
2. 结果解读

结果显示年龄(age)和性别(sex)的P值>0.1，而卡氏评分(ph.karno)的P值<0.05，提示年龄和性别满足PH假设，卡氏评分不满足PH假设；整体检验P值<0.05，也提示总体不满足PH假设。

(三) 构建AFT模型

R软件survival包提供了构建AFT模型的函数survreg()。AFT模型对生存时间的对数构建回归模型，对应的残差可服从多种分布，常见的如韦布尔分布、正态分布和对数logistic分布等。本例展示了对数logistic分布的结果。

1. 构建AFT多因素模型

aft.fit1 = survreg(Surv(time, status) ~ factor(sex) + age + ph.karno, 
data = mydata, dist = "loglogistic")
anova(aft.fit1)

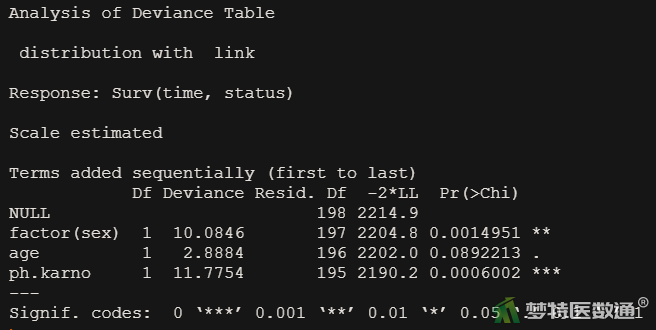
从图4可知， AFT模型分析了3个因素对于对数生存时间的影响，年龄(age)于对数生存时间的影响无统计学意义(P=0.089)，而其余两个因素有统计学意义(P<0.05)。

2. 构建AFT逐步回归模型

library(MASS) 
stepAIC(aft.fit1) 

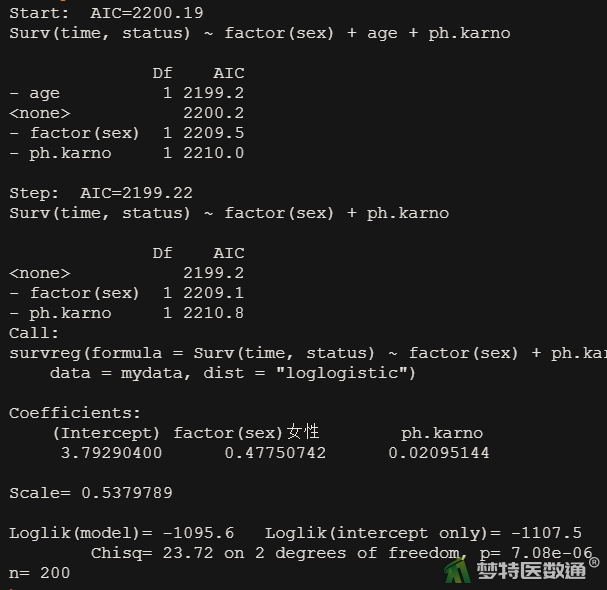
图5为基于AIC构建的逐步回归模型，模型中最终只有性别(sex)和卡氏评分 (ph.karno)两个自变量，和AFT多因素模型结果一致。

3. 构建AFT简洁模型

重新选择性别(sex)和卡氏评分(phkarno)建立AFT模型。

aft.fit2 = survreg(Surv(time, status) ~ factor(sex) + ph.karno,
                   data = mydata, dist = "loglogistic")
anova(aft.fit1, aft.fit2)

图6对比了模型1与模型2，对数似然比的差异无统计学意义(P=0.310)，说明使用性别(sex)和卡氏评分(ph.karno)两因素构建的模型是可行的。

summary(aft.fit2)

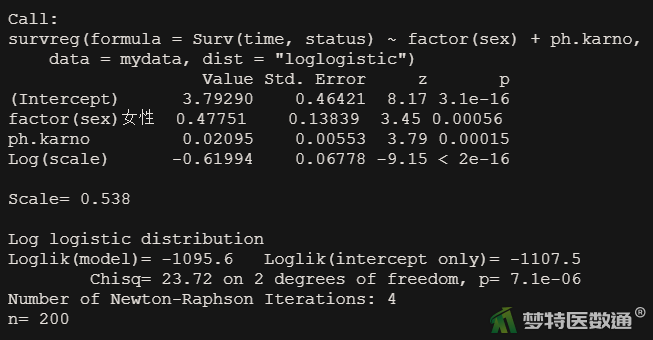
图7为多因素分析结果，与AFT逐步回归模型类似，表明性别(sex)和卡氏评分(ph.karno)两个因素于对数生存时间的影响有统计学意义(P<0.05)。

coef(aft.fit2)
exp(coef(aft.fit2))
exp(confint(aft.fit2))[-1,]

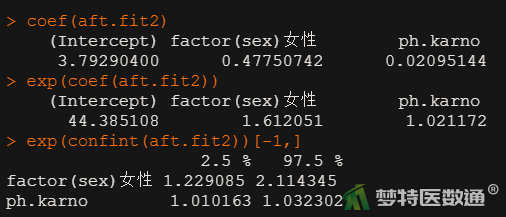
图8结果显示，对数生存时间与性别(sex)和卡氏评分(ph.karno)之间的回归方程为Log(T) = 3.793 + 0.478*sex(女性) + 0.021*ph.karno(卡氏评分)。这表明女性平均生存时长为男性的1.612倍(95%CI为1.229~2.114；P<0.001)；卡氏评分每增加一个单位，患者平均生存时长增加2.1% (95%CI为1.010~1.032；P<0.001)。

在Cox比例风险回归模型(Cox Proportional Hazard Regression Model)——R软件实现一文中，采用设立卡氏评分与时间的交互项进行数据分析，与年龄、性别一起建立含时依存协变量的Cox比例风险模型。分析结果为，性别的效应值HR为0.6159，表示女性死亡的风险比男性低38.4% (HR=0.616，95%CI为0.441~0.861；P=0.005)，年龄与生存结局的关联无统计学意义 (HR=1.012，95%CI：0.994~1.032；P=0.197)。卡氏评分的时依系数β(t)= -0.094+0.015×ln(t+20)，效应值HR=exp(-0.094+0.015×ln(t+20))。如，当时间为200天时，卡氏评分对应的HR=exp(-0.094+0.015×ln(200+20))= 0.987。

由于AFT模型是对生存时间的对数建立回归模型，而Cox模型是对风险函数建立回归模型，因此两个模型的回归系数所对应的流行病学意义有所不同。在AFT模型中，其回归系数的意义类似于线性回归模型回归系数的意义。

四、结论

本案例的目的是探究肺癌患者的性别、年龄和卡氏评分与生存结局的关系。首先构建了多因素Cox等比例风险回归模型并检验PH假设，结果显示模型不满足PH假设。进而构建不依赖PH假设的AFT模型，并展示了残差服从对数logistic分布模型的构建过程。

结果表明，年龄(age)与对数生存时间的影响尚无统计学意义(P=0.089)；女性平均生存时长为男性平均生存时长的1.612倍(95%CI为1.229~2.114；P<0.001)；卡氏评分每增加一个单位，患者平均生存时长增加2.1% (95%CI为1.010~1.032；P<0.001)。