回归分析中的交互效应分析(Interaction Effect Analysis)——R软件实现

关键字：R; 回归分析; 交互效应

在实际数据分析工作中，常会出现两个或多个因素之间存在相互作用的关系。如研究吸烟和饮酒等因素对高血压患病情况的影响时，吸烟和饮酒对因变量的影响可能存在相互作用的关系，这种情况下常可以采用交互效应分析，然后再采用分层分析详细了解各变量对结局的影响。

一、案例介绍

       为分析患者年龄和A、B、C三种抑郁症治疗方案与治疗效果的关系，同时判断治疗方案与患者年龄是否具有交互效应，本案例选取36例患者，采集患者年龄及治疗方案数据，因变量为治疗效果评分(score，评分越高效果越好)，自变量为年龄(age)、治疗方案(treatment)。变量信息见表 1。案例数据可从“附件下载”处下载。

二、问题分析

       本案例目的是分析患者年龄、治疗方案与治疗效果的关系，因变量为连续型变量，考虑采用多重线性回归分析，并在回归分析中创建患者年龄与治疗方法的交互项以分析二者是否具有交互效应。多元线性回归分析需要满足以下7条件：

条件1：样本量是自变量个数的5~10倍。本案例含5个自变量，分别为患者年龄、治疗方案变量(2个哑变量)和2个交互变量，而样本量为36，满足该条件。

条件2：自变量若为连续变量，需要与因变量之间存在线性关系。该条件需通过绘制散点图后判断。

条件3：各观测值之间相互独立，即残差之间不存在自相关。该条件需通过软件分析后辅助判断。

条件4：不存在显著的多变量异常值。该条件需通过软件分析后判断。

条件5：残差符合正态(或近似正态)分布。该条件需通过软件分析后判断。

条件6：残差大小不随所有变量取值水平的变化而变化，即方差齐性，可通过绘制残差图进行判断。

条件7：自变量之间无多重共线性，该条件需通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

##导入数据##
mydata <- read.csv('交互效应分析.csv')
str(mydata)

导入后的结果见图1。

##重新定义分组变量##
mydata$treatment <- factor(mydata$treatment, labels = c("A", "B", "C"))  #将变量“treatment”设置为因子变量并为各水平赋值标签
mydata$treatment <- relevel(mydata$treatment, ref = "C") #将治疗方案C设置为参照组
View(mydata)

案例数据见图2。

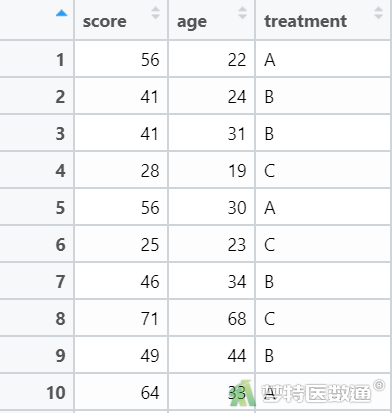
(二) 适用条件判断

1. 条件2判断(线性关系检测)

绘制患者年龄与治疗效果评分的散点图，其中患者年龄为连续变量。

(1) 软件操作

library(ggplot2)
ggplot(mydata,aes(x=age,y=score))+geom_point(size=4,aes(color=treatment))+stat_smooth(method="lm",se=TRUE)+theme(axis.title.x =element_text(size=20), axis.title.y=element_text(size=20))+theme(axis.text.x =element_text(size=20), axis.text.y=element_text(size=20))

(2) 结果解释

       图3为绘制的散点图，可知年龄和治疗效果评分之间呈线性关系，满足条件2。

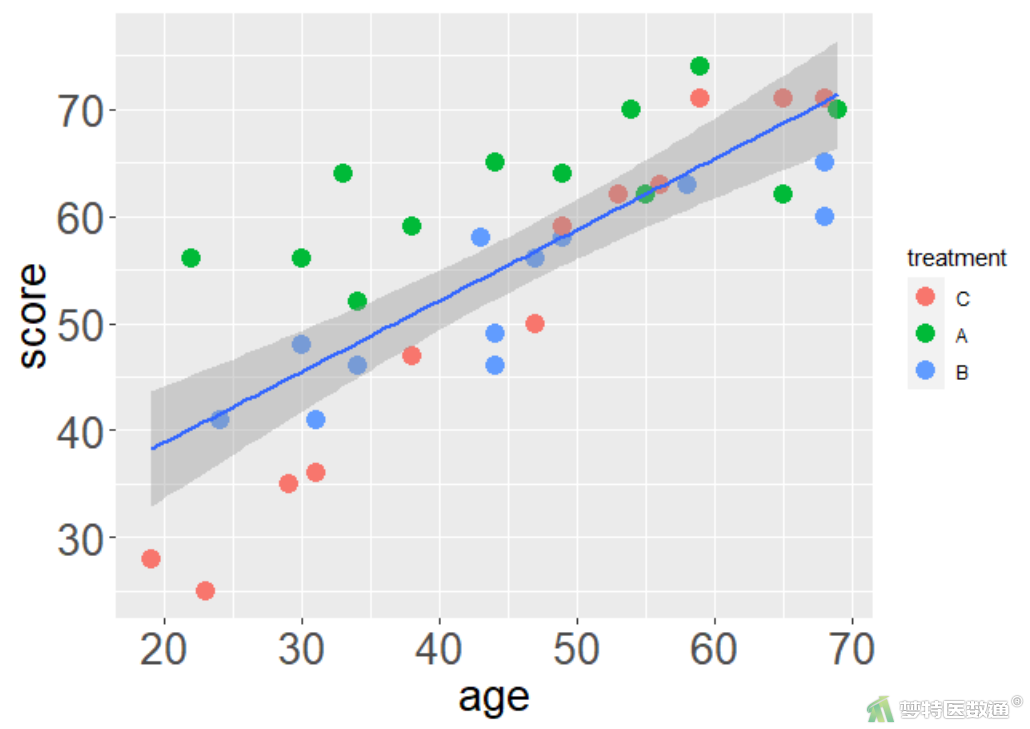
2. 条件3判断(各观测值之间相互独立)

Durbin-Watson检验通常用来检测残差是否存在自相关，Durbin-Watson检验值分布在0~4之间，越接近2，观测值相互独立的可能性越大。需要注意的是，判断观测值是否独立，主要取决于研究设计和数据收集阶段的质量控制，Durbin-Watson检验用于辅助判断。

(1) 软件操作

library(car)
durbinWatsonTest(lm(score~age+treatment+treatment*age,data=mydata))

(2) 结果解读

       图4为Durbin-Watson检验结果，可知DW=1.812，P=0.508，表明观测值相互独立，满足条件3。

3. 条件4判断(异常值判断)

Cook’s距离用于判断强影响点是否为因变量异常值点，一般认为当D（最大Cook’s距离）<0.5时，不是异常值点；当D>0.5时，是异常值点。

(1) 软件操作

lm.reg<-lm(score~age+treatment+treatment*age,data=mydata)
cook<-cooks.distance(lm.reg) #计算Cook距离
max(cook) #显示最大Cook距离

(2) 结果解读

       由图5可知，D=0.182834<0.5，表明模型中不存在显著异常值，满足条件4。

4. 条件5判断(残差正态性检测)

Shapiro-Wilk检验用于检验残差正态性。

(1) 软件操作

lm.reg<-lm(score~age+treatment+treatment*age,data=mydata)
shapiro.test(lm.reg$residuals) 

(2) 结果解读

       图6为Shapiro-Wilk检验结果，可知W=0.974，P=0.549，提示残差服从正态分布，满足条件5。

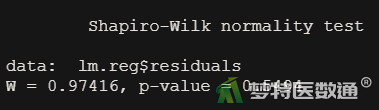
5. 条件6判断(残差方差齐性检测)

(1) 软件操作

par(mfrow=c(1,2),pin = c(2,3)) 
plot(lm.reg$residuals)
plot(mydata$age,lm.reg$residuals)

(2) 结果解读

       图7为残差图，可知各图中残差分布较为均匀，并未出现特殊的分布形式(如漏斗或者扇形)，提示残差的方差齐，满足条件6。

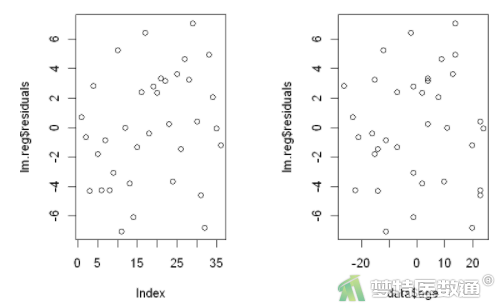
6. 条件7判断(多重共线性检测)

       含有交互效应的回归分析，常伴有多重共线性问题，因此需要对多重共线性问题进行考察，并根据情况对数据进行调整分析。采用VIF (variance inflation factor，方差膨胀因子)判断模型是否存在严重共线性，一般认为VIF<10时，自变量间不存在严重共线性。

(1) 软件操作

 library(car)
lm.reg<-lm(score~age+treatment+treatment*age,data=mydata)
vif(lm.reg)

(2) 结果解读

图8为VIF计算结果，可知年龄（VIF=1.601）、治疗方案（VIF=3.279）、交互效应（VIF=3.414）的VIF均<10，满足条件7。

(三) 含交互效应的线性回归

1. 软件操作

上述去中心化后的共线性检测过程已经使用lm函数拟合了线性回归。

summary(lm.reg)

2. 结果解读

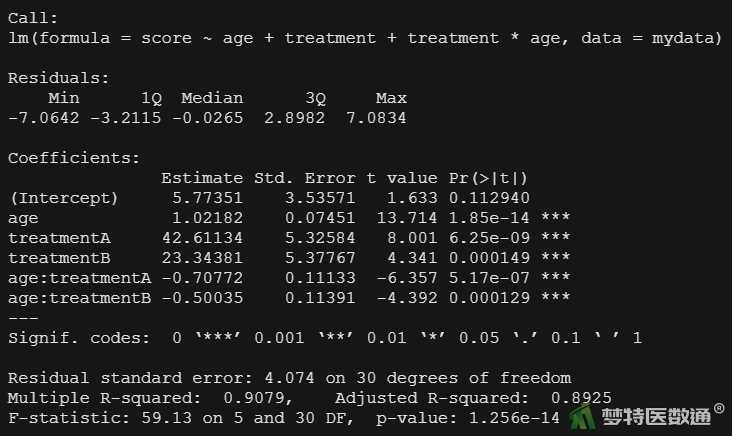
图9为线性回归拟合结果，可以看出模型残差标准误(Residual standard error)为4.074；拟合优度指标决定系数R²=0.908，提示自变量可以解释90.8%的因变量变异；调整自变量个数后R²=0.893，提示调整自变量个数后自变量可以解释89.3%的因变量变异。

       回归模型截距项为5.774 (P= 0.113)，表示所有自变量为0时的因变量取值，并无实际意义；患者年龄age非标准化系数为1.022 (P<0.001)，在不考虑交互项的前提下，表示年龄每增加1岁，因变量增加1.022分；哑变量treatment_A非标准化系数为42.611 (P<0.001)，在不考虑交互项的前提下，表示相比采用C方案患者，采用A方案因变量增加42.611分；哑变量treatment_B非标准化系数为23.344 (P<0.001)，在不考虑交互项的前提下，表示相比采用C方案患者，采用B方案因变量增加23.344分；交互项age*treatment_A非标准化系数为-0.708 (P<0.001)，交互项age*treatment_B非标准化系数为-0.500 (P<0.001)，交互项具有统计学意义，提示患者年龄与治疗方案存在交互效应。

       回归方程为：

       模型解读：

• 当采用A治疗方案时，回归方程为：

提示采用A治疗方案时年龄每增加一岁，治疗评分提高0.314分。

• 当采用B治疗方案时，回归方程为：

提示采用B治疗方案时年龄每增加一岁，治疗评分提高0.522分。

• 当采用C治疗方案时，回归方程为：

提示采用C治疗方案时年龄每增加一岁，治疗评分提高1.022分。

四、小结

       本研究的目的是分析患者年龄、治疗方案与治疗效果的关系，同时分析治疗方案与患者年龄是否具有交互效应，鉴于因变量“治疗效果评分”为连续变量，采用线性回归分析进行分析，并创建治疗方案与患者年龄的交互项以分析二者的交互效应。

       通过散点图可以观察到age与因变量总体呈现线性关系，Durbin-Watson检验表明观测值相互独立，Cook’s距离表明模型中不存在显著异常值，残差服从正态分布和方差齐性，所有自变量符合多重共线性的要求。本案例数据符合线性回归对数据的适用条件要求。

模型残差标准误(Residual standard error)为4.074；决定系数R²=0.908，提示自变量可以解释90.8%的因变量变异；调整自变量个数后R²=0.893，提示调整自变量个数后自变量可以解释89.3%的因变量变异。

患者年龄age非标准化系数为1.022 (P<0.001)，在不考虑交互项的前提下，表示年龄每增加1岁，因变量增加1.022分；哑变量treatment_A非标准化系数为42.611 (P<0.001)，在不考虑交互项的前提下，表示相比采用C方案患者，采用A方案因变量增加42.611分；哑变量treatment_B非标准化系数为23.344 (P<0.001)，在不考虑交互项的前提下，表示相比采用C方案患者，采用B方案因变量增加23.344分；交互项age*treatment_A非标准化系数为-0.708 (P<0.001)，交互项age*treatment_B非标准化系数为-0.500 (P<0.001)，交互项具有统计学意义，提示患者年龄与治疗方案存在交互效应。

       回归方程为：