简单局部加权回归(Simple Locally Weighted Regression)——R软件实现

关键词：R软件;局部加权线性回归; 局部加权回归; loess; lowess

普通线性回归通常是基于最小二乘法(OLS)进行计算，需要数据满足残差正态、齐性等条件。但实际应用中，数据有时并不满足普通线性回归的前提条件，或者会出现严重欠拟合现象，此时可使用局部加权回归(lowess)进行数据分析。

一、案例介绍

为探究某中药经典名方在降血压方面的治疗效果，临床入组100例患者，采集在服用不同剂量下患者的收缩压数据，因变量为收缩压(SBP)，自变量为每日服用剂量(dosage)。案例可从“附件下载”处下载。

二、问题分析

本案例研究某中药经典名方在降血压方面的治疗效果，因变量为连续型数据，考虑采用回归分析探究因变量与自变量之间的关系。经线性回归分析后发现，无论是在模型拟合程度、残差标准误等方面均不是很理想，考虑使用局部加权线性回归进行分析(见下文分析)。局部加权线性回归需满足以下3个条件：

条件1：因变量为连续型变量。本案例中因变量SBP为连续型变量，符合要求。

条件2：各观测值之间相互独立。该条件可通过软件分析后辅助判断。

条件3：自变量不存在显著异常值。该条件通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

data <- read.csv('局部加权线性回归.csv') #导入数据
View(data) #查看数据(图1)

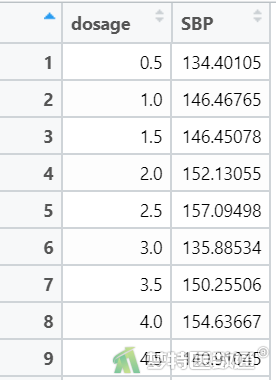
str(data) # 查看数据框结构(图2)

(二) 绘制散点图

绘制因变量与自变量的散点图。

library(ggplot2)
ggplot(data,aes(x=dosage,y=SBP))+geom_point(size=3)+theme(axis.title.x =element_text(size=20), axis.title.y=element_text(size=20))+theme(axis.text.x =element_text(size=20), axis.text.y=element_text(size=20))

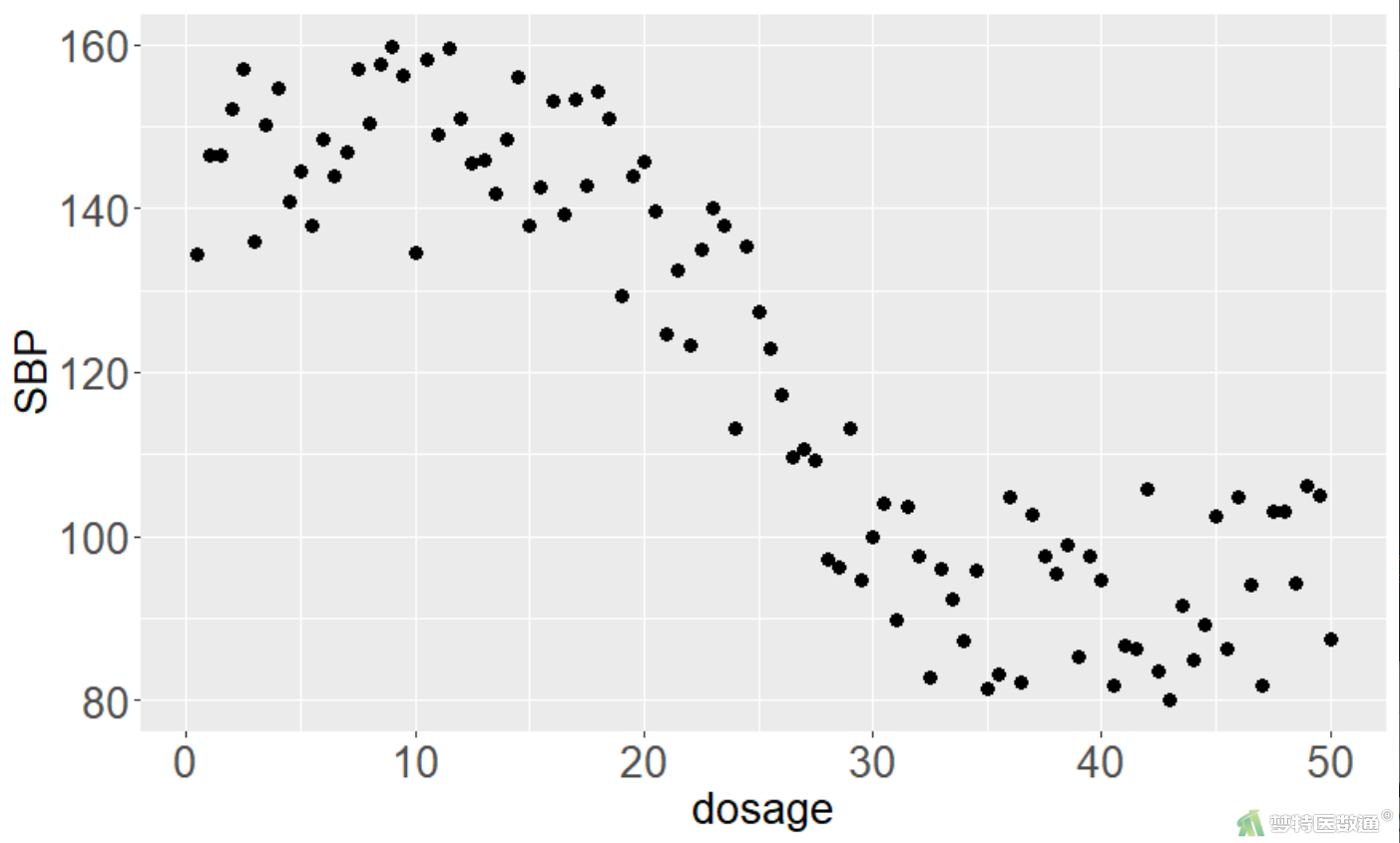
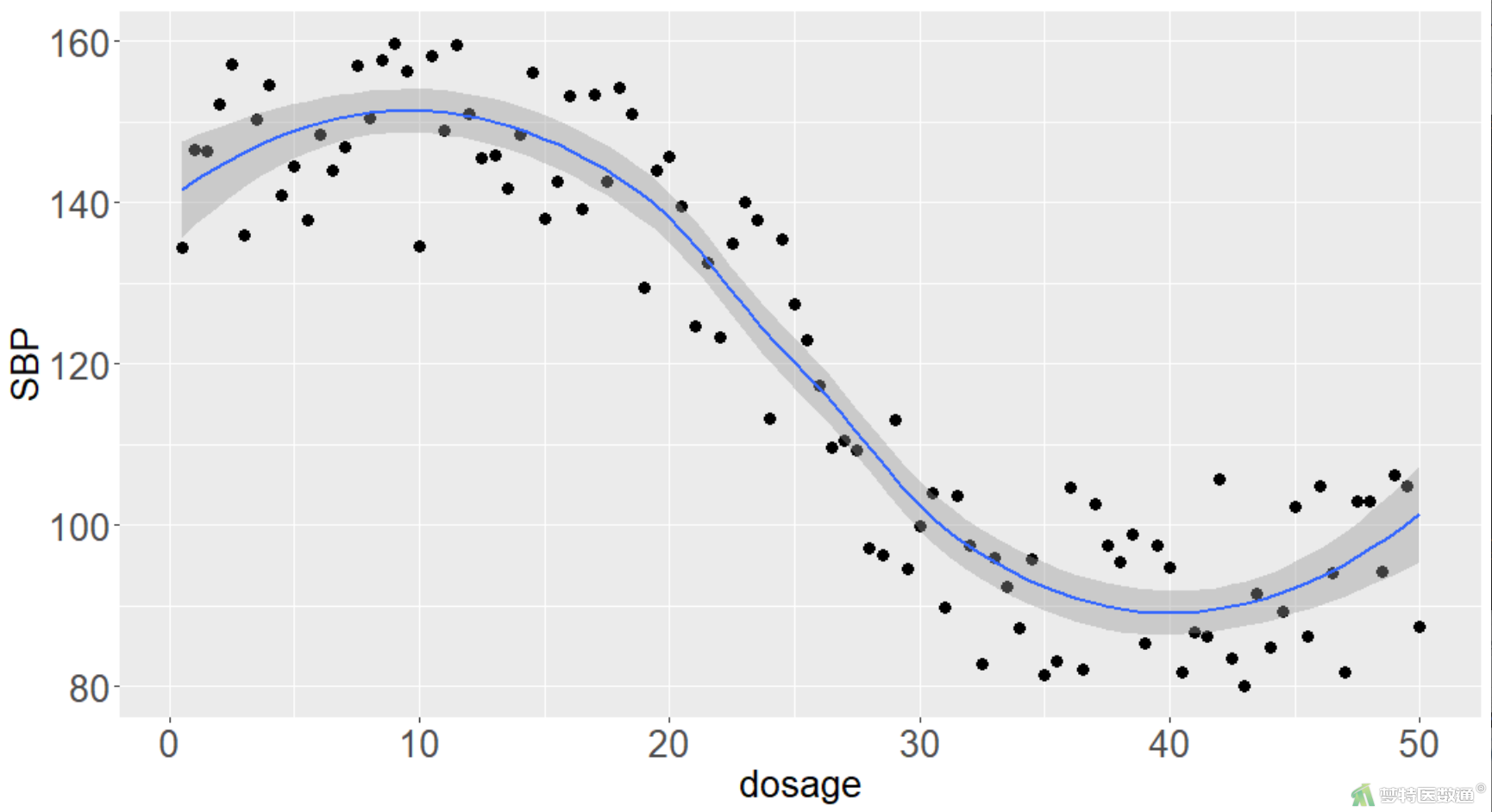
由图3可知自变量与因变量之间呈现倒S形的曲线回归。

(三) 线性回归

1. 软件操作

若使用lm函数进行线性回归拟合(图4)，并绘制回归曲线(图5)，结果见下文。

##线性回归拟合##
lmfit <- lm(SBP~dosage,data = data)
summary(lmfit)

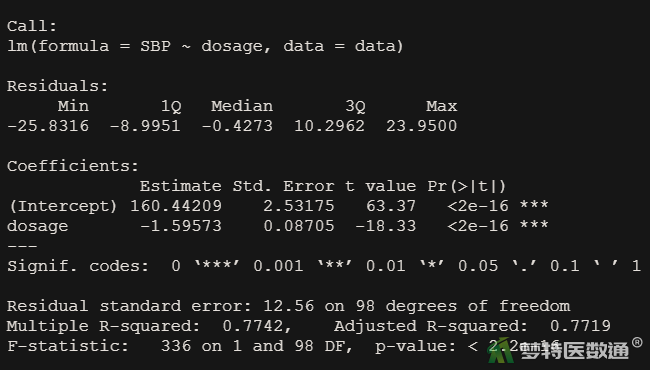
##查看回归拟合曲线##
ggplot(data,aes(x=dosage,y=SBP))+geom_point(size=3)+stat_smooth(method = 'lm',se = T)+annotate("text",x=45,y=155,label="atop(R^2==0.772)",size = 8,parse=T)+theme(axis.title.x =element_text(size=20), axis.title.y=element_text(size=20))+theme(axis.text.x =element_text(size=20), axis.text.y=element_text(size=20))

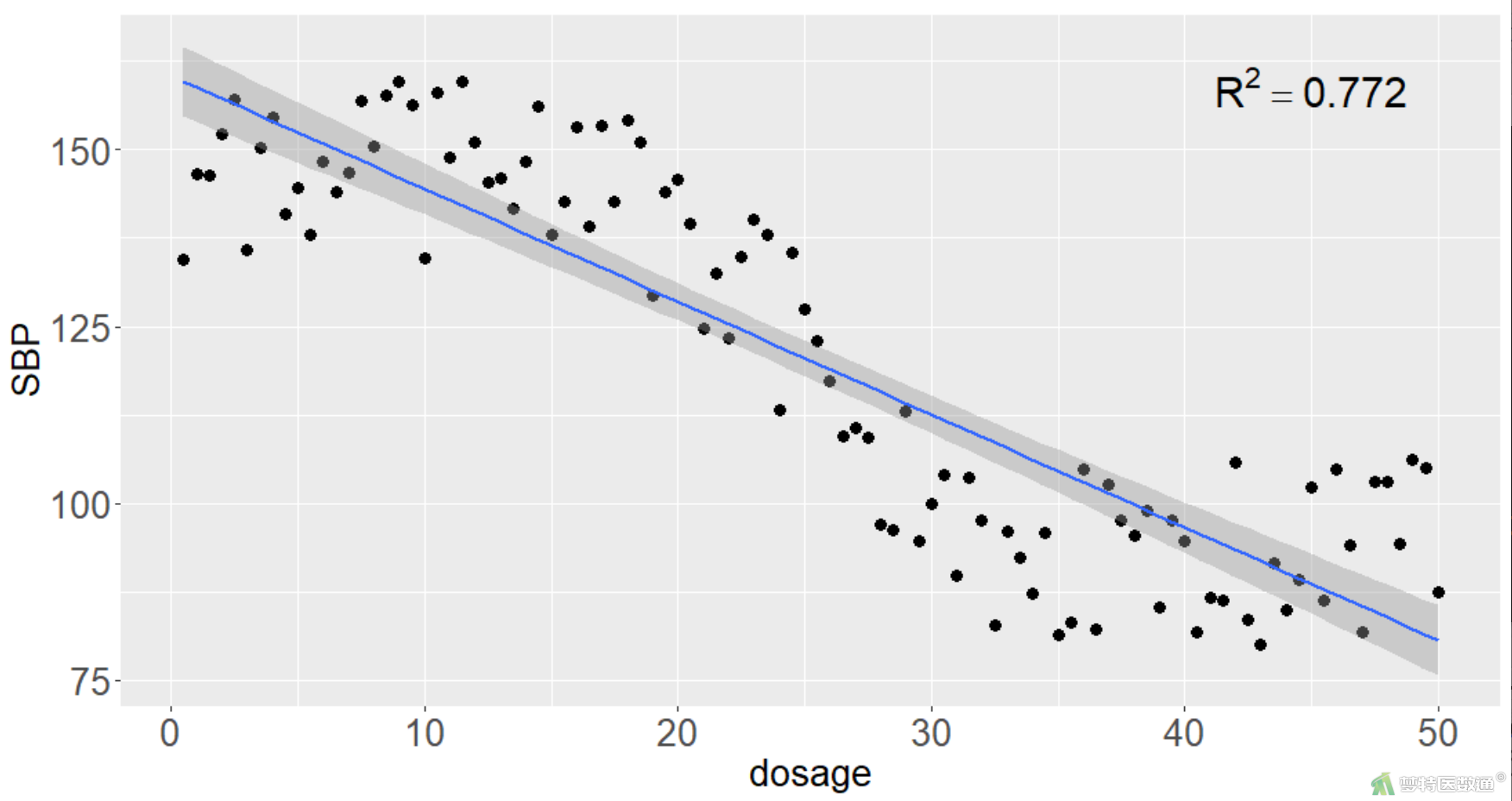
2. 结果解读

从图4线性回归拟合结果可以看出，模型残差标准误(residual standard error)为12.56，调整后R²为0.772；从图5拟合曲线可以看出，不少数据存在偏差，模型整体拟合情况一般。可尝试使用局部加权线性回归进行回归模型拟合。

(三) 局部加权回归

1. 软件操作

(1) 初始模型拟合

使用loess函数实现局部加权回归，在局部加权回归中，比较重要的参数为数据子集的获取范围(即span，数值越大表明选择的数据子集越多，默认值为0.75)。

##初始模型拟合##
loessfit <- loess(SBP ~ dosage,data = data,span=0.75)
summary(loessfit)

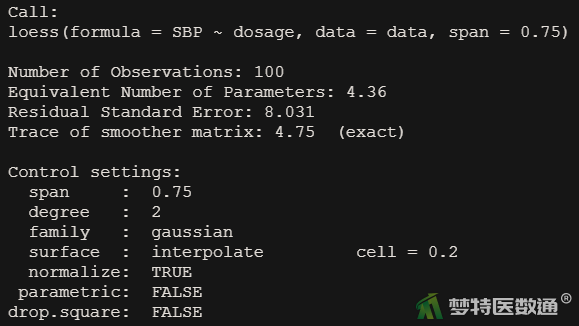
从图6可知，使用局部加权线性回归分析，模型残差标准误为8.031，比线性回归明显降低。

##绘制模型拟合曲线##(结果见图7)
ggplot(data,aes(x=dosage,y=SBP))+geom_point(size=3)+stat_smooth(method = 'loess',formula=y~x,span=0.75,se = T)+theme(axis.title.x =element_text(size=20), axis.title.y=element_text(size=20))+theme(axis.text.x =element_text(size=20), axis.text.y=element_text(size=20))

(2) span值的选择

span表示数据子集的获取范围，数值越大表明选择的数据子集越多，默认为0.75，但默认值并不一定是模型最优取值。通常情况下采用交叉验证估计获取模型最优span取值。判断标准采用GCV准则，计算公式如下：

\(G C V=\frac{1}{n} \frac{\sum_{i=1}^{n}\left(y_{i}-\widehat{y}_{l}\right)^{2}}{\left(1-\frac{v_{i}}{n}\right)^{2}}\)

       其中n为样本量，\(y_{i}\)为第i个真实值，\(\widehat{y}_{i}\)为第i个预测值，\(v_{i}\)为帽子矩阵的迹。

loess_loss <- function(s){
    model_fit <- loess(formula = SBP~dosage,data = data,span=s)
    gcv <- mean((model_fit$fitted-data$SBP)^2)/((1-model_fit$trace.hat/(length(data$SBP)))^2)
    return(gcv)
}  #定义-gcv准则计算函数
optim <- optimize(loess_loss, interval = c(0.01, 99))  #定义优化器
print(optim)  #查看结果(图8)

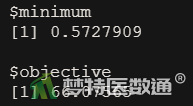
其中optim$minimum为span最佳取值，这里为0.5727909。

(3) 最佳模型

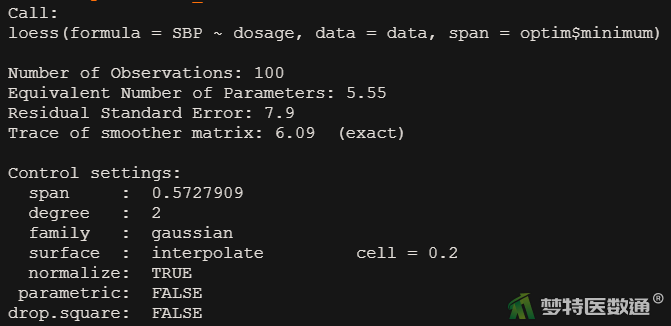
根据最佳span值，重新拟合模型(图9)，结果见图10。

loessfit_best <- loess(SBP ~ dosage,data = data,span=optim$minimum)
summary(loessfit_best)

##绘制拟合曲线##
ggplot(data,aes(x=dosage,y=SBP))+geom_point(size=3)+stat_smooth(method = 'loess',formula=y~x,span=optim$minimum,se = T)+theme(axis.title.x =element_text(size=20), axis.title.y=element_text(size=20))+theme(axis.text.x =element_text(size=20), axis.text.y=element_text(size=20))

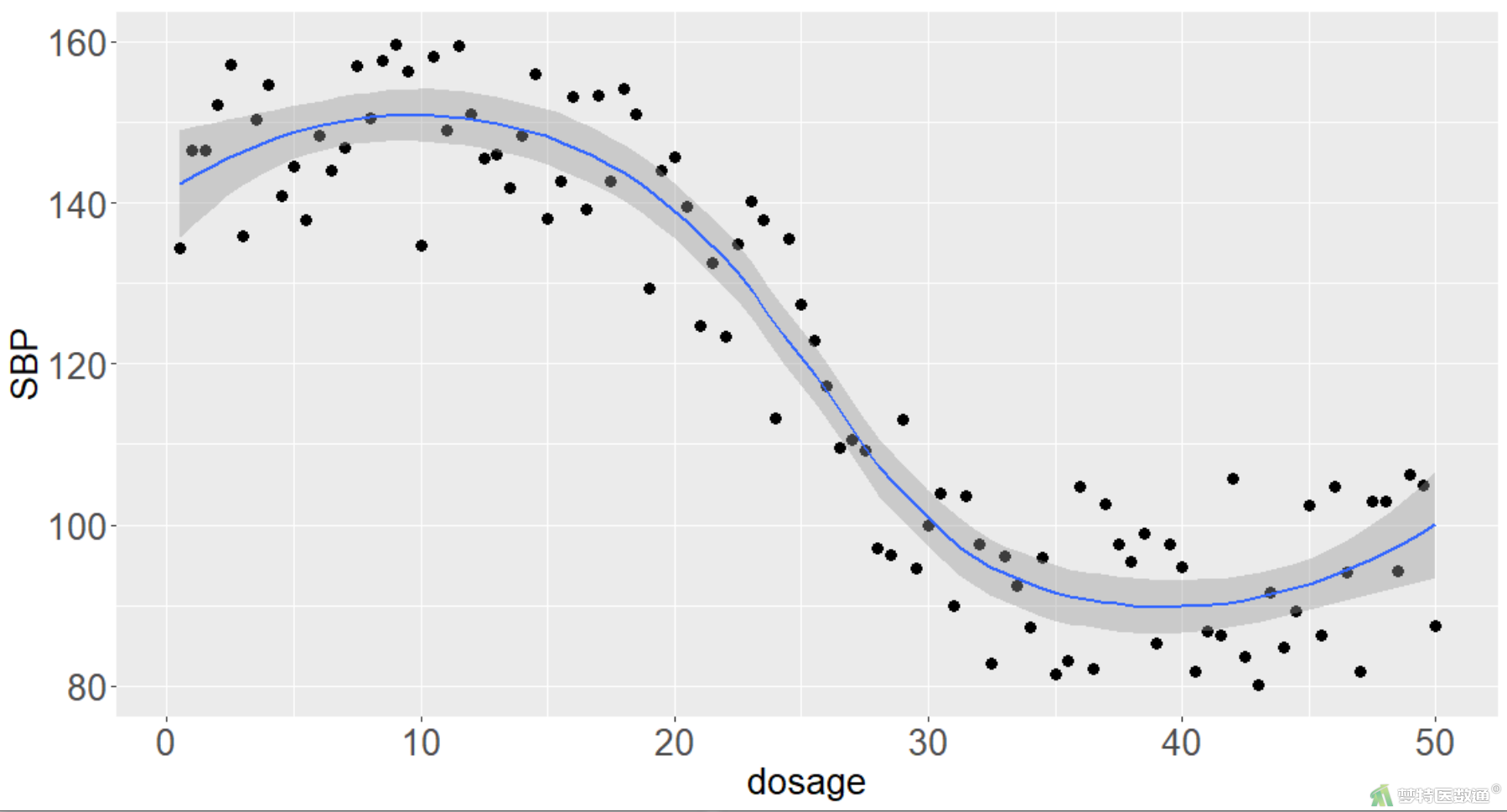
从图9可知，与最佳模型和初始模型比较，模型残差标准误从8.031进一步降低至7.9。

2. 适用条件判断

(1) 独立性考察

Durbin-Watson检验通常用来检测残差是否存在自相关，Durbin-Watson检验值分布在0~4之间，越接近2，观测值相互独立的可能性越大。需要注意的是，判断观测值是否独立，主要取决于研究设计和数据收集阶段的质量控制，Durbin-Watson检验一般用于辅助判断。

① 软件操作

library(car)
model_best = loess(SBP ~ dosage,data = data,span=0.57279087929112)
print(sprintf('Durbin-Watson检验值：%s',durbinWatsonTest(model = model_best$residuals)))

② 结果解读

       从图 11可知，DW Statistic为2.312，说明观测值相互独立，满足条件2。

(2) 异常值考察

① 软件操作

##绘制两组变量箱型图##
data_tab = data.frame(group = c(rep('SBP',each=nrow(data)),rep('dosage',each=nrow(data))),values = c(data$SBP,data$dosage))
labels <- c("SBP","dosage")   #设置分组标签
boxplot(data_tab$value ~ data_tab$group, names = labels, 
        xlab = "group", ylab = 'values')  #分组绘制箱线图

② 结果解读

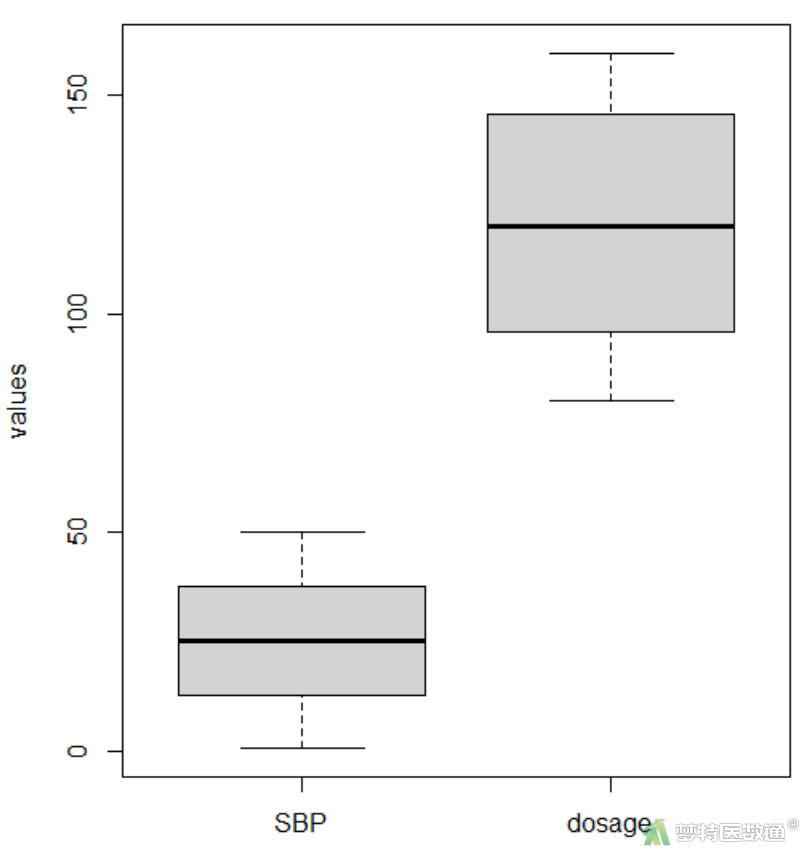
从图 12可知，本案例数据未发现明显异常值，满足条件3。

3. 结果解读

从简单局部加权线性回归拟合结果可以看出，模型残差标准误(residual standard error)为7.9，相比线性回归模型残差标准误12.56明显下降；从拟合曲线可以看出，模型整体拟合效果良好，且表明某中药经典名方的服用剂量与降血压效果呈现S型关系。