2×2 Fisher确切概率法(2×2 Fisher’s Exact Test)——jamovi软件实现

关键词：jamovi; 卡方检验; Fisher确切概率法; Fisher精确检验; 费希尔确切概率法; 费希尔精确检验

一、案例介绍

某医师为研究术前使用抗菌药A预防术后感染的效果，将34例行人工全膝关节置换术的患者随机分为试验组(代码为1)和对照组(代码为2)，收集患者术后感染的情况[分为阳性(代码为1)和阴性(代码为0)]，对数据的变量进行标签赋值后部分数据见图1。本文案例可从“附件下载”处下载。问两组患者术后感染率有无差别？

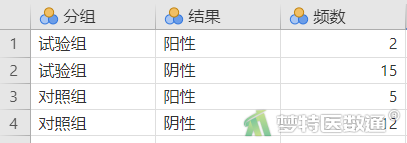
二、问题分析

本案例的分析目的是比较两组患者术后的感染率有无差异，由于总例数(34例)<40，因此需要考虑使用Fisher精确检验。但需要满足2个条件：

条件1：分组变量和观察变量均为二分类变量，本案例数据满足该条件。

条件2：观测值相互独立，本案例数据满足该条件，研究对象的术后感染情况互不干扰。

三、软件操作及结果解读

(一) 适用条件判断

本案例的数据满足上述条件。

(二) 统计描述及推断

1. 软件操作

① 选择“分析”—“频数”—“独立样本χ²关联检验”(图2)。

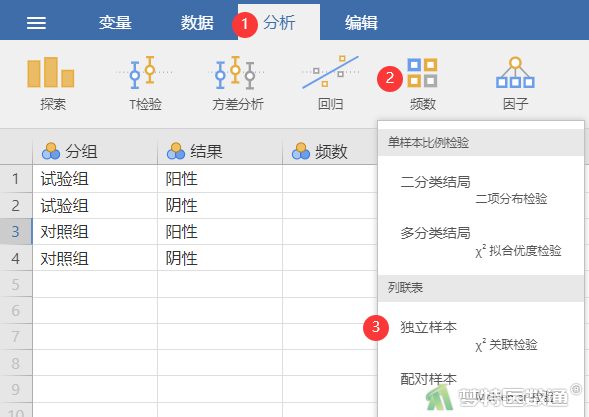
② 按照图3将“分组”、“结果”和“频数”选入右侧变量框内。

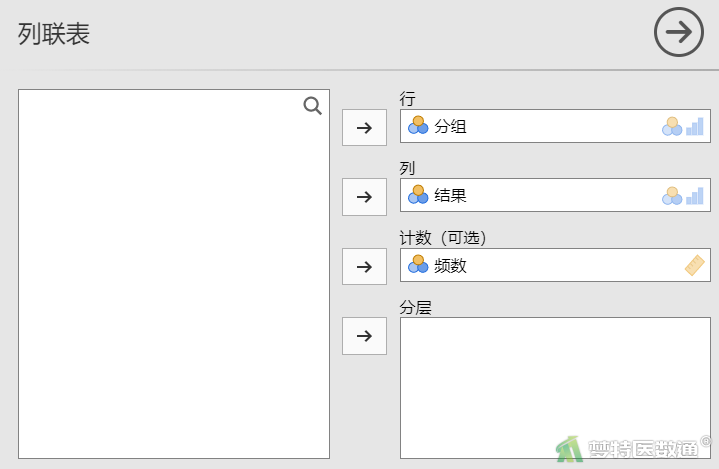
③ 在“单元格”下的“计数”中勾选“实际频数”和“理论频数”，在“百分比”中勾选“行”(见图4)。

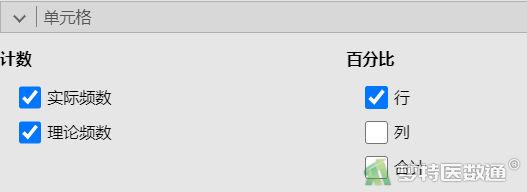
④ 在“统计”中勾选“Fisher’s精确检验”(图5)。

⑤ 在“绘图”中勾选“条形图”、“堆积”、“百分比”、“行”或“列”(图6)。

2. 结果解读

(1) 统计描述

表1中“列联表”中给出了试验组、对照组组和全部患者术后感染阳性/阴性频数、理论频数、行百分比，可知试验组和对照组的术后感染率分别为11.8%和29.4%，34例患者的总体感染率为20.6%。将两组术后感染率的可视化为堆积百分比条形图，见图7。

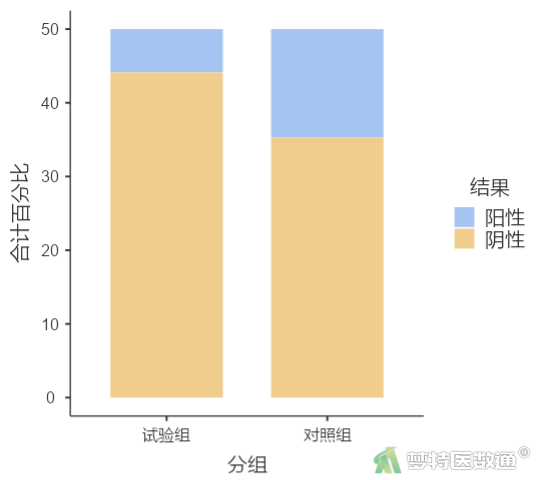
(2) 统计学推断

表2“χ² 检验”给出了Fisher精确检验的P值，由P=0.398可知按照α=0.05的检验水准，两组患者术后感染率的差异无统计学意义，尚不能认为试验组组和对照组的术后感染率不同。

四、结论

本研究采用2×2 Fisher精确检验对两组患者术后感染率进行比较分析，由于总例数(34例)<40，数据满足Fisher精确检验的条件。分析结果显示，试验组患者的术后感染率为11.8%，对照组的术后感染率为29.4%，Fisher精确检验的P值为0.398>0.05，提示两组患者的术后感染率的差异无统计学意义，尚不能认为两组患者的术后感染率不同。

五、知识小贴士

当2×2列联表资料出现下列情况时，需要使用Fisher精确检验：

• 样本量N<40。
• 期望频数T<1。
• χ²检验或连续校正χ²检验所得P值接近检验水准α。
• 关于χ²检验的更多内容详见χ²检验的注意事项——使用技巧。