四格表资料的Fisher确切概率法(2×2 Fisher's Exact Test)——理论介绍

关键词：卡方检验; Fisher确切概率法; Fisher精确检验; 费希尔确切概率法; 费希尔精确检验

一、适用条件

条件1：分组变量和观察变量均为二分类变量。

条件2：观测值相互独立。

二、基本思想

在四格表周边合计数固定不变的情况下，计算图1内4个实际频数变动时的各种组合之概率P_i；再按检验假设用单侧或双侧的累积概率P，依据所取检验水准α作出推断。

(一) 各组合概率P_i的计算

在四格表周边合计数不变的条件下，当四格表内实际频数a、b、c、d有一个取值确定，则整个频数的组合即确定。因此图1内4个实际频数a、b、c、d变动的组合数共有“周边合计中最小数+1”个。如C1=3，则a的可能取值为0，1，2，3。第i种组合的概率P_i公式如下，服从超几何分布：

n=a＋b＋c＋d

！为阶乘符号，n为总例数，i为各种组合的序号。各种组合的概率P_i服从超几何分布，且 \( \Sigma_{\mathrm{P}_{\mathrm{i}}}=1 \) 。

(二) 累计概率P_i的计算

定P_i (i=1，2，…)对应于a从小到大的概率，记现有样本四格表的概率为P^*。

1. 单侧检验：现有样本四格表及其以左的所有四格表组合的累计概率为左侧概率，记为P_L；现有样本四格表及其以右的所有四格表组合的累计概率为右侧概率，记为 P_R。若备择假设 H₁为 π₁>π₂，则 P_单侧=P_R；若H₁为 π₁＜π₂，则 P_单侧=P_L。

2. 双侧检验：计算满足 P_i≤P^*条件下的各种组合之四格表的累计概率。若遇到 a + b = c+ d 或 a + c = b + d 时(即行合计相等或列合计相等)，四格表内各种组合的序列呈对称分布，此时可只计算满足条件的单侧累计概率，然后乘以2即得双侧累计概率。

三、案例数据

某医师为研究术前使用抗菌药A预防术后感染的效果，将34例行人工全膝关节置换术的患者随机分为试验组(Trial group)和对照组(Control group)，收集患者术后感染的情况[分为阳性(Positive)和阴性(Negative)，数据见图2。问两组患者术后感染率有无差别？

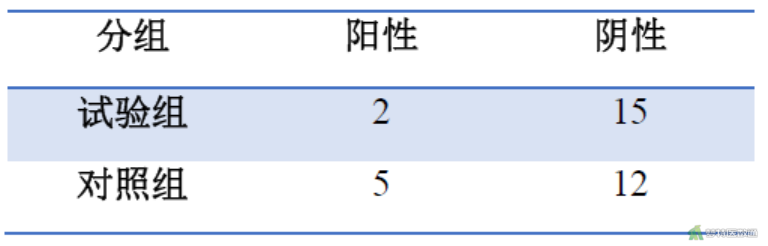
四、假设检验

本例n<40，且有两个格子的理论频数为3.5<5，宜用四格表资料的Fisher确切概率法，其假设检验的步骤如下：

(一) 建立检验假设，确定检验水准

H₀：π₁=π₂，即两组患者术后感染率相同

H₁：π₁≠π₂，即两组患者术后感染率不相同

α=0.05

(二) 计算概率

在周边合计不变的条件下，只需依次增减样本四格表第1个格子a的数据，即得到8个四格表，并按a由小到大排列，结果见图3。

1. 计算现有样本四格表的概率P*及各组合下四格表的概率P_i

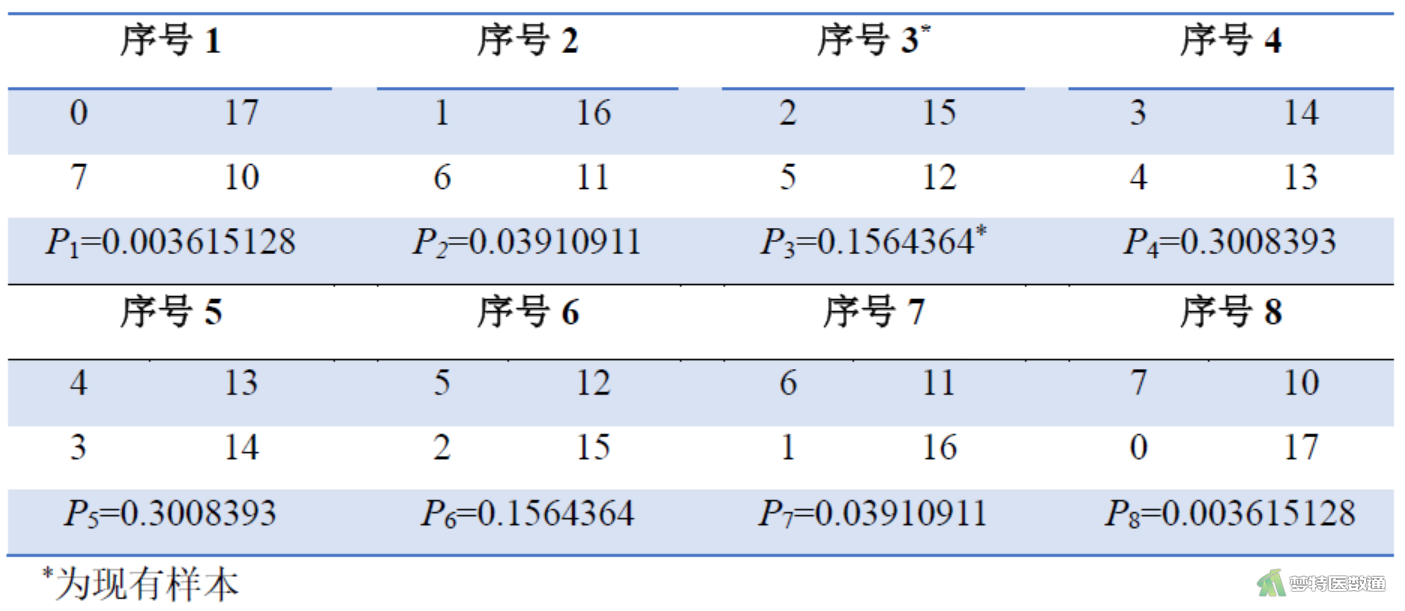
由图3可知各种组合以i=4和i=5的组合为中心呈对称分布。本例P^*=0.1564364445。

2.计算满足 P_i≤P^*的所有四格表的累计概率

本例P₁、P₂、P₃、P₆、P₇和P₈满足条件，累计概率为：

P=P₁＋P₂＋P₃＋P₆＋P₇＋P₈=0.39832139

(三) 确定P值，作出推断结论

P＞0.05，α=0.05水准，不拒绝H₀，尚不能认为两组患者的术后感染率不同。