2×2 卡方检验(2×2 χ2 Test)——jamovi软件实现

关键词：jamovi; 卡方检验; 理论频数; 实际频数; 四格表

一、案例介绍

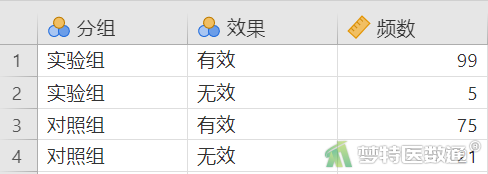
某中医院欲比较某经典名方控制高血压的效果。将200例高血压患者随机分到试验组(代码为1)和对照组(代码为2)，随访三个月后患者的血压控制情况[分为有效(代码为1)和无效(代码为0)]，对数据的变量进行标签赋值后部分数据见图1。本文案例可从“附件下载”处下载。问该经典名方控制血压的效果如何？

二、问题分析

本案例的分析目的是探究某经典名方控制血压的效果，即比较试验组与对照组血压控制率是否有差异，针对这种情况可以制作四格表，并进行2×2 χ²检验。但需要满足2个条件：

条件1：分组变量与观察变量均为二分类变量。本案例的分组变量和观察变量均为二分类变量，该条件满足。

条件2：观察变量相互独立。本研究中各研究对象的观察变量都是独立的，不存在互相干扰的情况，该条件满足。

条件3：总例数≥40，且所有期望频数(理论频数)≥5。该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 适用条件判断

对于本案例数据，条件1和条件2均满足。但需要通过总例数和期望频数来选择具体的分析方法(Pearson χ²检验、连续校正χ²检验、Fisher精确检验)。这一判断过程通过统计描述来完成，详见下文。

(二) 统计描述及推断

1. 软件操作

① 选择“分析”—“频数”—“独立样本χ²关联检验”(图2)。

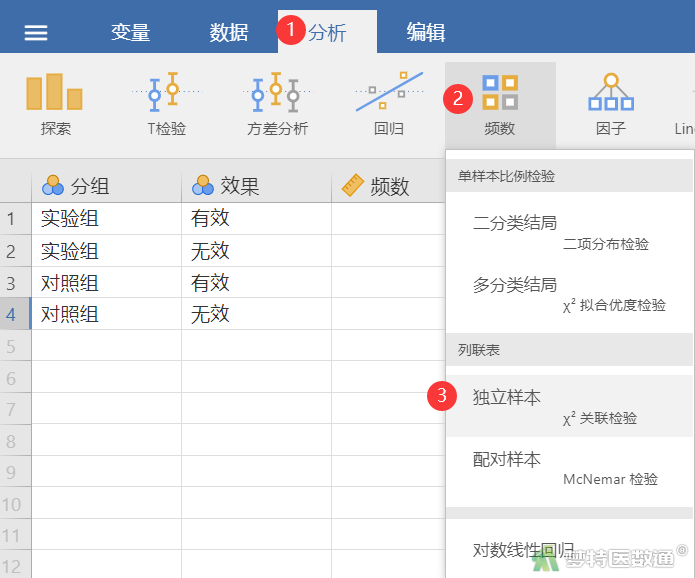
② 将“分组”、“效果”和“频数”选入右侧对应的变量框内(图3)。

③ 在“单元格”下的“计数”中勾选“实际频数”和“理论频数”，在“百分比”中勾选“行”或“列”(图4)。

④ 在“统计”中勾选“χ²”、“连续性校正χ²”、“Fisher’s精确检验”(图5)。

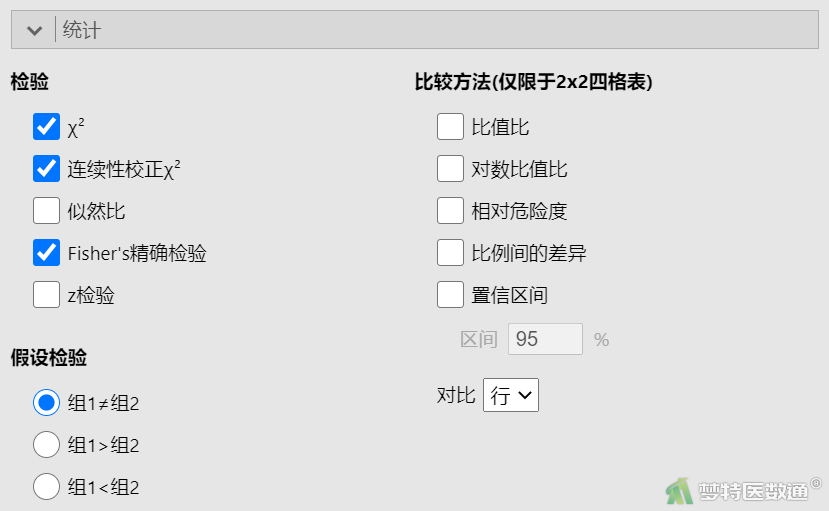
⑤ 在“绘图”中勾选“条形图”、“堆积”、“百分比”、“行”或“列”(图6)。

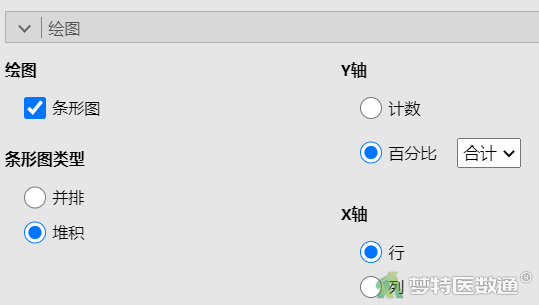
2. 结果解读

(1) 统计描述

表1“列联表”中给出了对照组和试验组的有效、无效例数及百分比、理论频数。由结果可知，对照组和试验组的血压控制率分别为78.1%和95.2%。总例数为200例，期望频数均>5。将两组有效率和无效率可视化为堆积的百分比条形图，见图7。

(2) 统计推断

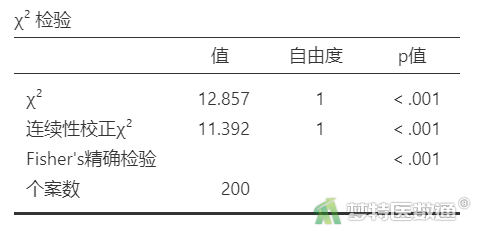
由表1可知，总例数为200例，期望值均>5。因此，检验结果可以采用表2中的第一行的Pearson χ²检验。Pearson χ²检验结果表明两组高血压患者的血压控制率的差异有统计学意义 (χ²=12.857，P<0.001)。Fisher's精确检验结果进一步验证了Pearson χ²检验的结论。

四、结论

本研究采用2×2 χ²检验(独立样本χ²检验)比较两组高血压患者血压控制率有无差别。数据满足2×2 χ²检验的条件，总例数为200例，期望值均>5，采用Pearson χ²检验结果。结果显示，试验组和对照组的血压控制率分别为95.2%和78.1%，差异有统计学意义(χ²=12.900，P<0.001)，试验组的血压控制率高于对照组。

五、知识小贴士

• 当总例数≥40，且所有期望频数(理论频数)≥5时，可使用Pearson χ²检验。当总例数≥40，有1个期望频数≥1且<5，可使用连续校正χ²检验。当总例数＜40或有1个期望频数＜1，需要使用Fisher精确检验。
• 无论总例数的大小及期望频数分布情况如何，Fisher精确检验均可使用。在计算机能够满足运行负荷的情况下，推荐使用Fisher精确检验。如果使用Pearson χ²检验或连续校正χ²检验得出的P值比较接近检验水准，建议采用Fisher精确检验。
• 关于χ²检验的更多内容详见χ²检验的注意事项——使用技巧。

六、分析小技巧

χ²检验的数据录入可分为两种：

• 第一种，即本案例所用的加权数据类型，将分组变量、观察变量、频数分别选到对应的变量框内进行分析。
• 第二种为非频数资料，只有分组变量和观察变量两列，每一行为一个患者的数据，在分析时只需将分组变量和观察变量选入右侧变量框即可。