2×2 Fisher确切概率法(2×2 Fisher’s Exact Test)——SAS软件实现

关键词：SAS; 卡方检验; Fisher确切概率法; Fisher精确检验; 费希尔确切概率法; 费希尔精确检验

一、案例介绍

某医师为研究术前使用抗菌药A预防术后感染的效果，将34例行人工全膝关节置换术的患者随机分为试验组和对照组，收集患者术后感染的情况，分为阳性和阴性。问两组患者术后感染率有无差别？

首先进行数据录入，χ²检验的数据录入可分为两种：第一种为频数资料，需要设置分组变量、观察变量和频数变量，该形式在进行χ²检验时较为常见，进行统计分析前需要进行数据加权。第二种为非频数资料，只有分组变量和观察变量两列，每一行为一个患者的数据，该形式是在SAS软件中进行各种统计分析最常用的资料形式，进行χ²检验前不需要进行数据加权。

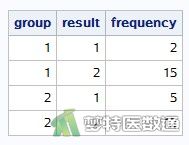
本案例的数据采用第一种录入方式。创建分组变量“Group”，赋值为“1”和“2”分别代表试验组和对照组。创建观察变量“Result”，赋值为“1”和“2”分别代表术后感染情况阳性和阴性。创建频数变量“Frequency”，记录各组不同感染情况的患者数。数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是探究术前使用抗菌药A预防术后感染的效果，即比较试验组与对照组术后感染率是否有差异，针对这种情况首先考虑可以制作四格表，并进行2×2 χ²检验。但当2×2列联表资料出现下列情况时，需要使用2×2 Fisher确切概率法：①样本量n<40；②期望频数T<1；③χ²检验或连续校正χ²检验所得P值接近检验水准α。本案例由于总例数为34例<40，因此考虑使用Fisher确切概率法。但需要满足2个条件：

条件1：分组变量和观察变量均为二分类变量，本案例数据满足该条件。

条件2：观测值相互独立，本案例数据满足该条件，研究对象的术后感染情况互不干扰。

三、软件操作及结果解读

(一) 适用条件判断

本案例的数据满足上述条件。

(二) 统计描述及推断

1. 软件操作

本案例为频数资料，需要先手动输入数据。

data mydata;
input group result frequency@@;
cards;
1 1 2 1 2 15 2 1 5 2 2 12
;
proc print noobs;
run;

结果如图1所示。

其次进行卡方检验，通过weight对frequency进行加权处理。

proc freq data=mydata;
weight frequency;
tables group*result/chisq expected;
run;

2. 结果解读

(1) 统计描述

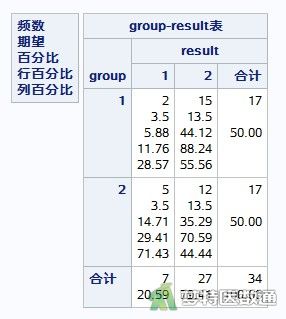
图2为“Group*Result Crosstabulation(组别*结果交叉表)”，给出了试验组和对照组的观察值、期望频数及组内占比。由结果可知，试验组和对照组的术后感染率分别为11.76%和29.41%。总例数为34例。

(2) 统计学推断

解读χ²检验结果时，遵循以下原则：①当总例数≥40，且所有期望频数(理论频数)≥5时，可使用Pearson χ²检验。②当总例数≥40，有1个期望频数≥1且<5，可使用连续校正χ²检验。当总例数＜40或有1个期望频数＜1，需要使用Fisher确切概率法。③无论总例数的大小及期望频数分布情况如何，Fisher确切概率法均可使用。在计算机能够满足运行负荷的情况下，推荐使用Fisher确切概率法。如果使用Pearson χ²检验或连续校正χ²检验得出的P值比较接近检验水准，建议采用Fisher确切概率法。

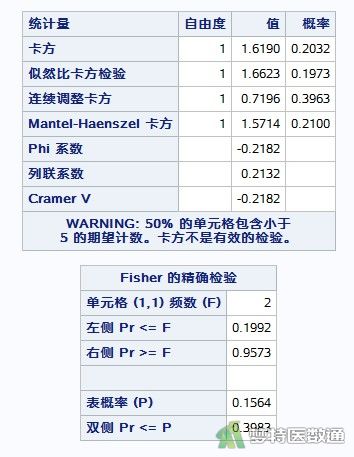
图3为本案例检验结果，其中列出了多种检验结果。表格下方的WARNING提示：“有50%的单元格包含小于5的期望计数，卡方不是有效的检验”，根据图2发现最小期望频数为3.5。同时因为本案例样本数为35，小于40，所以检验结果可以采用下方的Fisher’s Exact Test(Fisher的确切概率法)，此处给出了Fisher确切概率法的P值，由双侧检验P=0.3983可知按照α=0.05的检验水准，两组患者术后感染率的差异无统计学意义，尚不能认为试验组组和对照组的术后感染率不同。

四、结论

本研究采用2×2 Fisher确切概率法对两组患者术后感染率进行比较，由于总例数(34例)<40，需要使用Fisher确切概率法。分析结果显示，试验组患者的术后感染率为11.76%，对照组的术后感染率为29.41%，Fisher确切概率法的P值为0.3983>0.05，提示两组患者的术后感染率的差异无统计学意义，尚不能认为两组患者的术后感染率不同。