R×C 卡方检验(R×C χ² Test)——SAS软件实现

关键词：SAS; 列联表卡方检验; 多个率比较; 关联性检验; 列联系数

一、案例介绍

某科室回顾性研究推拿疗法、药物疗法和针灸疗法3种疗法治疗腱鞘炎的疗效。问3种疗法的有效率有无差别以及疗法与效果(分为有效和无效)的关联？

首先进行数据录入，χ²检验的数据录入可分为两种：第一种为频数资料，需要设置分组变量、观察变量和频数变量，该形式在进行χ²检验时较为常见，进行统计分析前需要进行数据加权。第二种为非频数资料，只有分组变量和观察变量两列，每一行为一个患者的数据，该形式进行χ²检验前不需要进行数据加权。

本案例的数据采用第一种录入方式。创建分组变量“Therapy (疗法)”，赋值为“1”、“2”、“3”，分别代表“推拿疗法(Manipulation)”、“药物疗法(Drug)”和“针灸疗法(Acupuncture)”。创建观察变量“Effect (效果)”，赋值为“1”和“2”分别代表“有效(Effective)”和“无效(Noneffective)”。创建频数变量“Frequency”，记录多种疗法下不同效果的患者数。数据见图1。本文案例可从“附件下载”处下载。

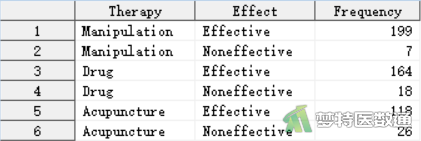
二、问题分析

本案例的分析目的是比较三种疗法治疗腱鞘炎的疗效，也就是比较三组患者有效率的差异，同时分析两者的关联性。可以采用R×C χ²检验。但需要满足4个条件：

条件1：分组变量和观察变量均为分类变量，至少有一个无序多分类变量，且观察变量不是有序多分类变量。本案例的行变量疗法为无序三分类变量，列变量疗效为二分类变量，本案例数据满足该条件。

条件2：观测值之间相互独立，本案例的观测值均是相互独立，本案例数据满足该条件。

条件3：样本量足够大，要求每个格子内的期望频数均应>1，且期望频数<5的格子数不宜多于总格子数的1/5。

条件4：两个变量是同一随机样本的两种属性，本案例是回顾性分析疗法与效果的关联，所采用的疗法与效果均为已发生的事件，可以算作两种属性，该条件满足。

三、软件操作及结果解读

(一) 导入数据

①利用LIBNAME语句建立SAS逻辑库关联，注意逻辑库名称要求，即最大长度8字符，必须以字母或下划线“_”开始，可以是字母、数字和下划线的任意组合。具体代码如下：

ibname mydata 'D:\mydata';

通过这一步骤，SAS能够识别引号中的物理位置，将逻辑库建立在该目录下，同时在以下过程中新建的SAS表格便可以永久储存在该位置，便于反复读取和使用。先运行该代码使其生效。

②利用PROC IMPORT语句导入文件，代码如下：

proc import out= mydata.example
datafile=" D:\mydata\R×C卡方检验.csv"
dbms=csv replace;
getnames=yes;
run;

该过程在mydata逻辑库中生成example数据集，数据文件由DATAFILE=选项指定，DBMS=选项指定其数据库类型。该案例中初始数据集为csv文件，故而使用“dbms=csv”指定。如果已经存在相同名称的SAS数据集，即可使用REPLACE选项进行覆盖。GERNAMES=YES选项指定从第2行开始读取数据，将数据集的首行变量名作为SAS数据集的变量名。

(二) 适用条件判断

本案例数据满足条件1、2和4，条件3的判断详见统计描述及推断。

(三) 统计描述及推断

1. 整体检验

(1) 软件操作

运用FREQ语句进行检验，具体代码如下所示：

proc freq data= mydata.example;
tables Therapy*Effect/chisq expected;
weight Frequency;
exact chisq;
run;

TABLES语句以“Therapy”和“Effect”两变量形成R×C表格，以WEIGHT语句为“Frequency”资料进行加权处理。TABLES语句中CHISQ选项进行χ²检验，EXPECTED选项输出各组期望频数。EXACT语句可进行χ²检验。

(2) 结果解读

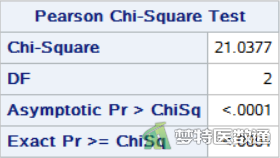
图2为“Table of Therapy by Effect (治疗方式与结果交叉表)”，给出了三种不同治疗方法各治疗效果的观察值、期望频数及组内占比。由结果可知，推拿疗法(Manipulation)、药物疗法(Drug)和针灸疗法(Acupuncture)的有效率分别为96.60%、90.11%和81.94%。总例数为532例，每个格子的第二行为期望频数(Expected)，均大于5。

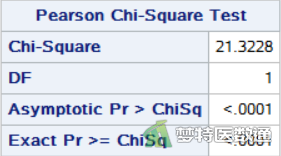
图3“Pearson Chi-Square Test (χ²检验)”给出了R×C χ²检验的统计量、自由度和P值。由图2中的总频数和每个格子的期望频数可知该案例数据满足条件3，所以假设检验的P值可采用Chi-Square结果，即三种疗法有效率的差异有统计学意义(χ²=21.0377，P<0.0001)。

2.事后检验(两两比较)

对于R×C χ²检验，其结果只能说明各组的率或构成比整体上有无统计学差异，并不能说明哪两组之间的差异是否有统计学意义。因此，需要进行事后检验，即事后两两比较。SAS中可以通过卡方分割法，即将三组率或构成比的比较拆分成多个两组率或构成比的比较，需要校正检验水准α'=α/m，其中m=k(k-1)/2，k为分组数。本案例为3个分组，拆分成3个两组率的比较；取α=0.05，则α=0.05/3=0.017。具体操作步骤如下所示：

(1) 软件操作

以针灸疗法(Acupuncture)和药物疗法(Drug)两组比较为例，新建数据集mydata.example1，用IF语句保留推拿疗法(Manipulation)和药物疗法(Drug)两组数据，再用与前一步骤中相似的FREQ语句进行卡方检验：

data mydata.example1;
set mydata.example;
if Therapy in ("Manipulation","Drug") then output;
run;
proc freq data= mydata.example1;
tables Therapy*Effect/chisq expected;
weight Frequency;
exact chisq;
run;

同理，药物疗法(Drug)和针灸疗法(Acupuncture)两组数据比较：

data mydata.example2;
set mydata.example;
if Therapy in ("Drug","Acupuncture") then output;
run;
proc freq data= mydata.example2;
tables Therapy*Effect/chisq expected;
weight Frequency;
exact chisq;
run;

推拿疗法(Manipulation)和针灸疗法(Acupuncture)代码如下：

data mydata.example3;
set mydata.example;
if Therapy in ("Manipulation","Acupuncture") then output;
run;
proc freq data= mydata.example3;
tables Therapy*Effect/chisq expected;
weight Frequency;
exact chisq;
run;

(2) 结果解读

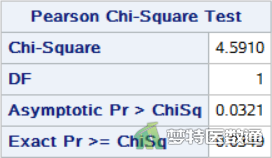
图4、图5和图6分别给出了三个组别进行两两比较时形成的交叉表，相应的观察值、期望频数及组内占比等。

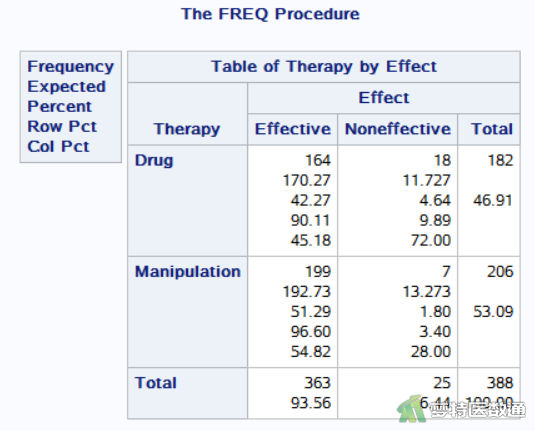
图7、图8和图9“Pearson Chi-Square Test (χ²检验)”分别给出了推拿疗法(Manipulation)和药物疗法(Drug)、药物疗法(Drug)和针灸疗法(Acupuncture)、推拿疗法(Manipulation)和针灸疗法(Acupuncture)有效率的比较结果，精确P值分别为0.0120、0.0349、<0.0001。可知，按照α'=0.017的检验水准，推拿组与药物组有效率的差异有统计学意义，药物组与针灸组有效率的差异无统计学意义，推拿组与针灸组有效率的差异有统计学意义。

四、结论

本研究采用R×C χ²检验(R×C χ² Tests)对三种疗法治疗腱鞘炎的有效率进行比较，结果显示推拿疗法的有效率为96.60%、药物疗法的有效率为90.11%、外用膏药的有效率为81.94%，三种疗法有效率的差异有统计学意义(χ²=21.0377，P<0.0001)，表明三种疗法的有效率不全相同。

采用χ²分割法，按照α'=0.017的检验水准进行两两比较，发现药物组与针灸组有效率的差异无统计学意义(P=0.0349)。推拿组与药物组有效率的差异有统计学意义(P=0.0120)，推拿组与针灸组有效率的差异有统计学意义(P<0.0001)。                                           

五、分析小技巧

• 多重比较一般分为事前检验(Prior tests)和事后检验(Post hoc tests)。事前检验是指在数据收集之前便决定了要通过多重比较来考察多个组与某个特定组之间的差别，多根据专业意义设定比较的策略。如果是事前检验，不论整体分析的结果如何，均可进行比较，并且一般不需要对检验水准进行太多修正。事后检验只有在总体χ²检验得到有统计学意义的P值后才有必要进行，是一种探索性分析。对于事先未计划的多重比较(即事后检验)，各组间的差别只是一种提示，要确认这种差别最好重新设计实验。

六、知识小贴士

• R×C χ²检验要求每个格子内的期望频数均应>1，且期望频数<5的格子数不宜多于总格子数的1/5；如果期望频数太小，最好的办法是增加样本量以增加期望频数；若增加样本量有困难，则可使用Fisher确切概率法；若分组较多，可以合理的合并若干组，以增加期望频数。