在前面文章中介绍了无金标准的诊断试验的评价方法Bland-Altman法的理论知识(无金标准的诊断试验研究——概述),本篇文章将实例演示在MedCalc软件中使用Bland-Altman法检验两种方法间一致性评价的操作步骤。
关键词:无金标准诊断试验; Bland-Altman图; D-A图; MedCalc; 一致性
一、案例介绍
为检测脑脊液中某指标(X)的含量,分别使用A、B两种方法检测36份脑脊液样本(X)的含量,试分析两种方法检测的结果是否一致?
创建数值型变量“A方法”和“B方法”,分别表示用A和B方法检测出的指标(X)的含量。部分数据见图1,本文案例可从“附件下载”处下载。
二、问题分析
本案例的分析目的是评价两种诊断试验之间的一致性,由于检测指标为计量资料,因此可以考虑使用Bland-Altman法来分析。但需要满足5个条件:
条件1:两种诊断试验的指标均为连续型指标。本研究中用A和B方法检测的指标(X)均为连续变量,该条件满足。
条件2:两个诊断试验的指标应当是针对于同一个个体。本研究中同时用两种方法分别检测了36例脑脊液样本,两种方法的检测结果之间是对应关系,该条件满足。
条件3:两种诊断方法的结果差值呈正态分布。该条件需要通过分析进行判断。
条件4:两种诊断方法的D与A独立,其中D为两种诊断方法测量的差值,A为两种诊断方法测量的均值。该条件需要通过分析进行判断。
条件5:两种诊断方法测量差值的平均趋势在测量范围内保持不变,差值的分散程度在测量范围内保持一致。可通过两种方法测量差值的回归线与零刻度线是否平行进行判断。该条件可需要分析后判断。
三、适用条件判断
1. 条件3判断(正态性检验)
(1) 软件操作
- 在excel中先计算两种方法的差值,然后将数据导入MedCalc软件(图2)。
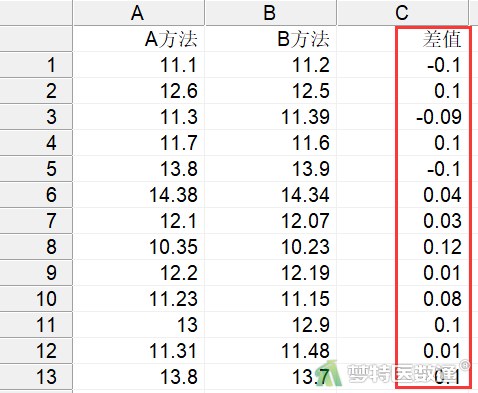
- 选择“统计”-“分布图”-“正态图”(图3)。
- 将变量“差值”选入“变量”,“选项”中勾选“QQ图”,“检验正态分布”中选择“Shapiro-Wilk检验”,点击“确定”(图4)。
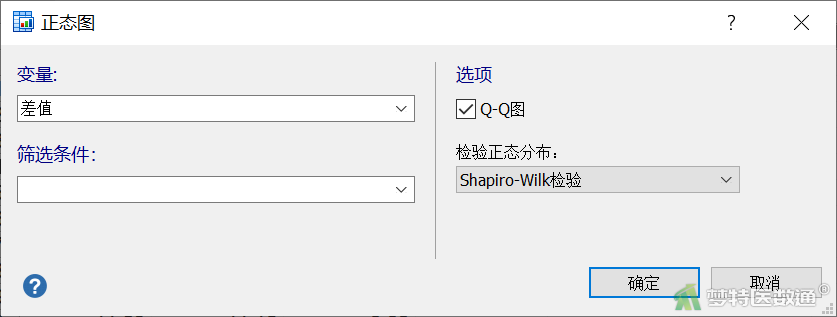
(2) 结果解读
由正态Q-Q图(图5)可知,差值基本围绕对角线分布,提示近似服从正态分布。正态性检验结果为W=0.9401,P=0.0513,也提示差值近似服从正态分布。满足条件3。更多正态性检验内容,可参考(医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现)。
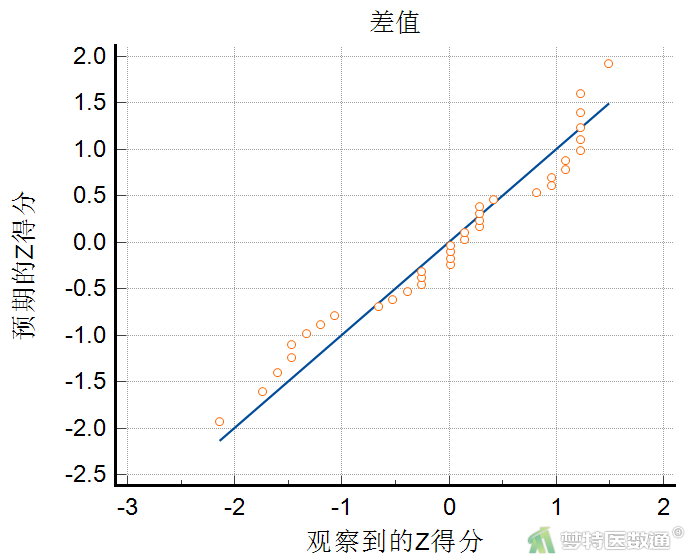

2. 条件4、5判断
详见下文。
四、Bland-Altman法分析
(一) 软件操作
- 在MedCalc软件中打开数据,选择“统计”—“方法对比和评估”—“Bland-Altman图”(图7)。
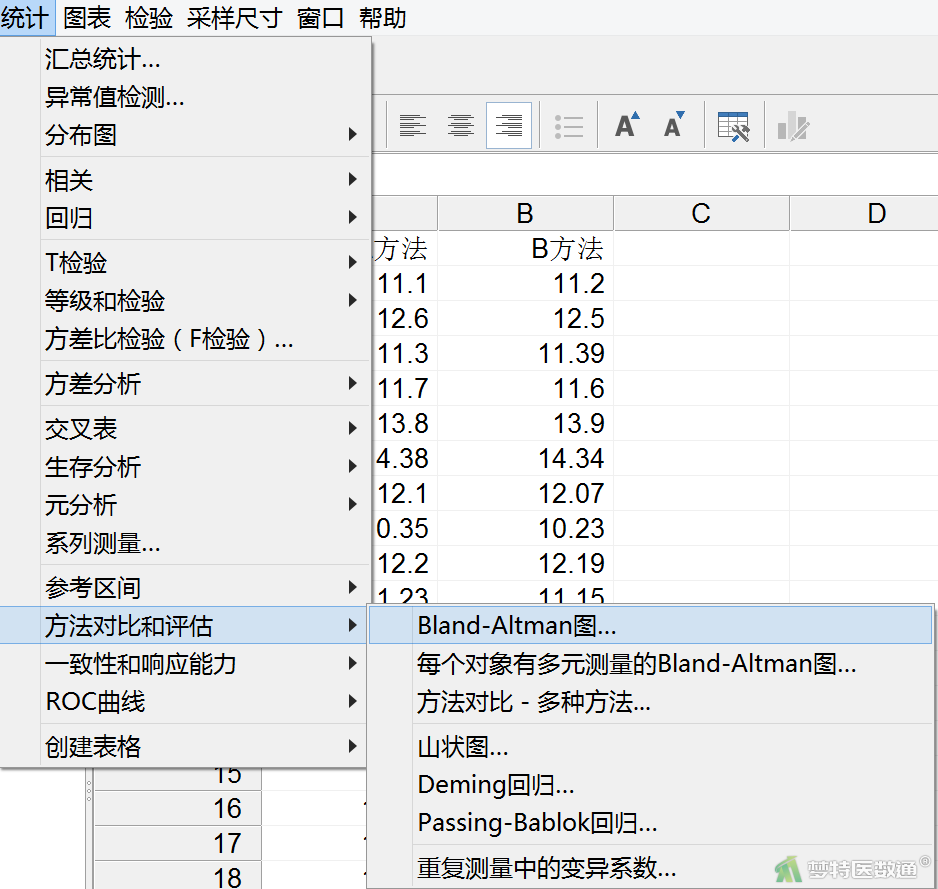
- 在“第一种方法”对话框中选择“A方法”,“第二种方法”对话框中选择“B方法”。“图表”下“图形对比(X轴)”选择“两种方法的平均值”,点击“绘制差异”。“选项”下“方法之间允许的最大差异”为临床上可接受指标(X)的差异的临界值范围,需要结合临床允许的误差设定界值,本例假设界值为“0.3”;勾选“画均等线(差异=0)”、“为95% CI的平均差画线”、 “为95% CI的一致性限制画线(A)”、“画差异的回归线” 和“95%置信区间”。点击“确定”(图8)。
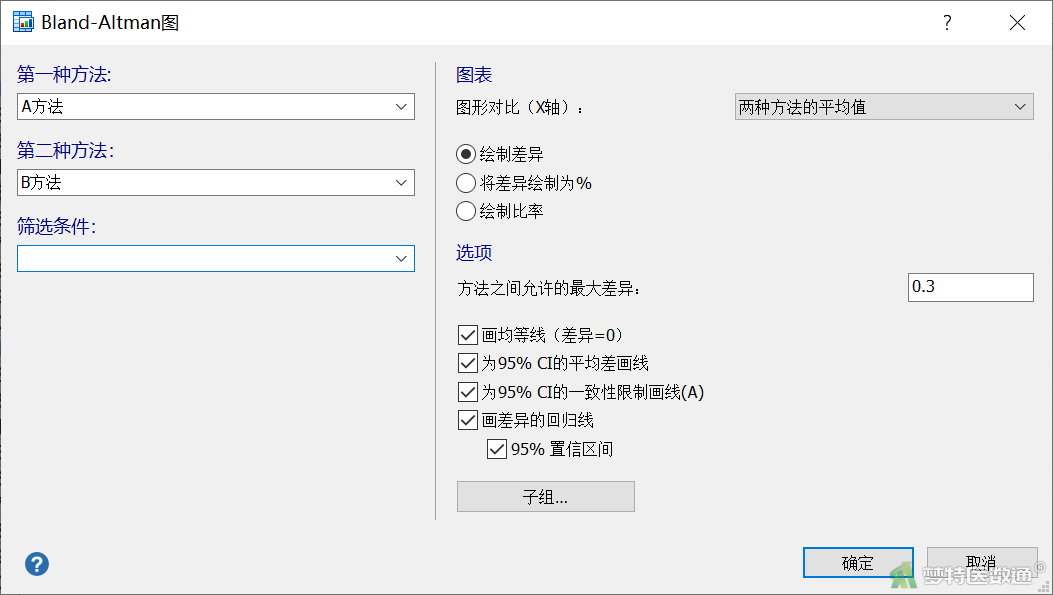
(二) 结果解读
1. 补充条件判断
图9为Bland-Altman图,可见图中散点分布均匀离散,未发现明显规律性,表明两种诊断方法的差值D与均值A独立,条件4满足。回归线(紫色虚线)基本与零刻度线平行,表明两种诊断方法测量差值的平均趋势在测量范围内保持不变,条件5满足。
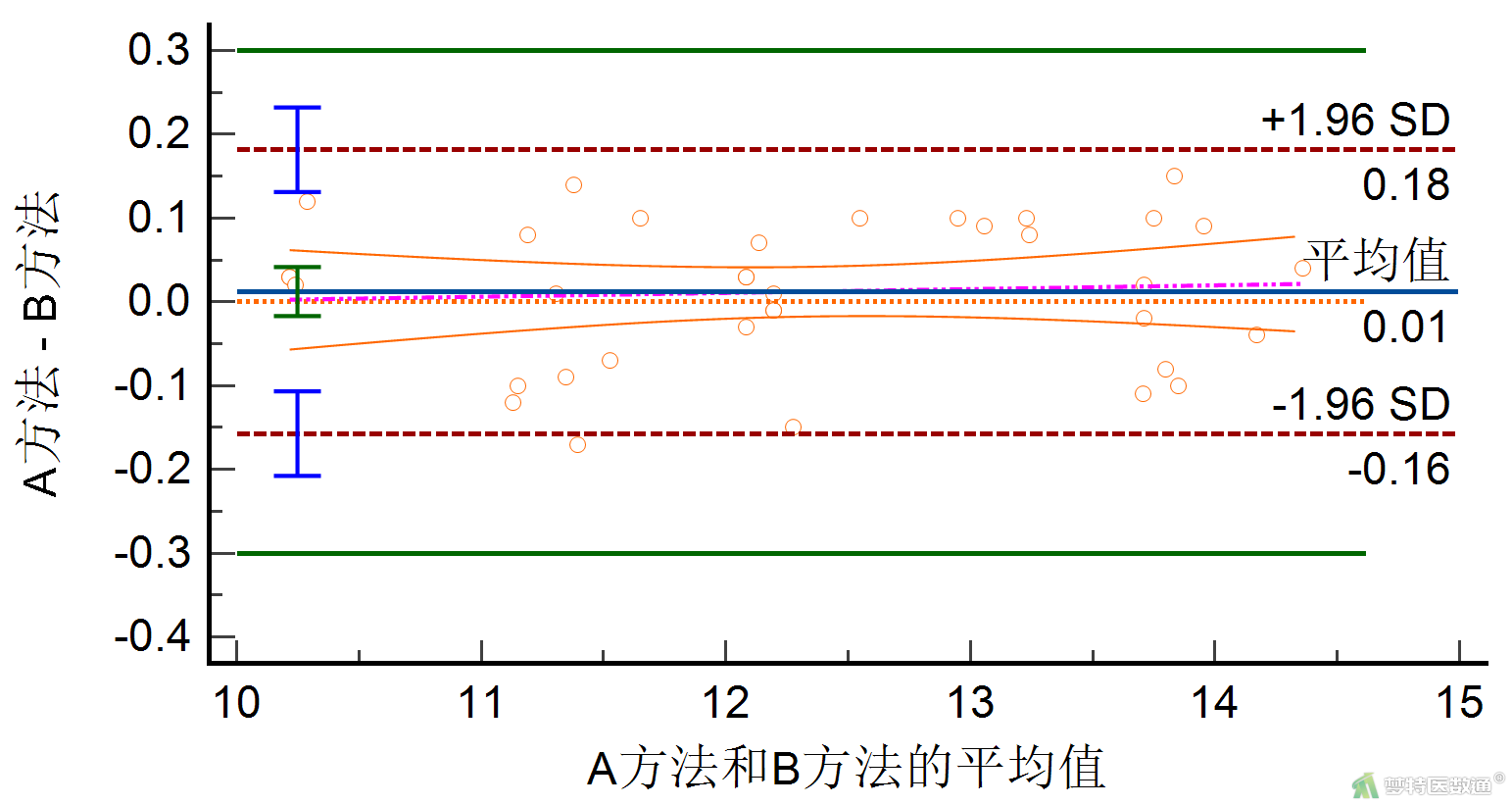
2. Bland-Altman分析结果解读
Bland-Altman图中橙色虚线为零刻度线,蓝色实线为平均值线、绿色竖线为平均值的95%CI,深咖啡色虚线为LoA线、蓝色竖线为LoA的95%CI,紫色虚线为回归线,两条绿色实线为专业上允许的最大差异线。
本例使用两种方法检测36个样本,从Bland-Altman图可见,有1个点(2.78%)落在LoA之外,但并无点落在LoA的95%CI之外,LoA的95%CI均位于专业上允许的最大差异线之内。可以说明两种方法测定结果一致性较好。
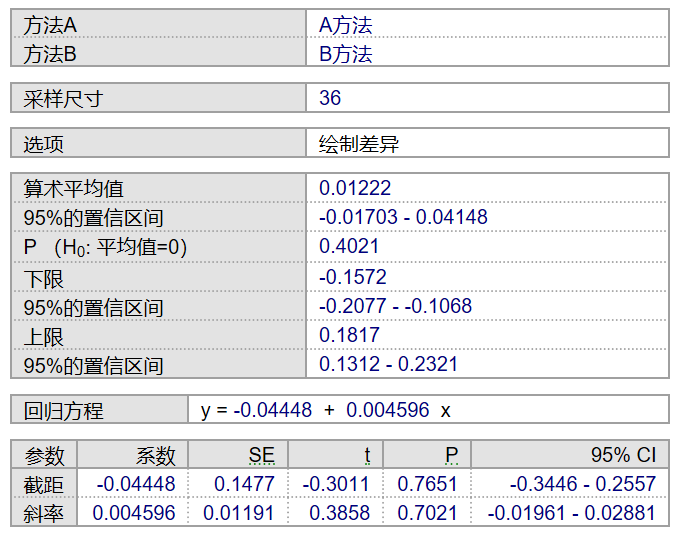
图10为Bland-Altman图的详细信息,两种方法测量结果的平均差为0.01222,95%CI为(-0.01703~0.04148),包含0。结合P=0.4021>0.05,可认为两种方法测量值的差异无统计学意义。Bland-Altman回归方程y = -0.04448+0.004596 x,方程总体截距和斜率的95%CI分别为(-0.3446~0.2557)和(-0.01961~0.02881),均包含0,P值均大于0.05,截距和斜率与0的差异无统计学意义,表明两种方法测量结果不存在比例差异。
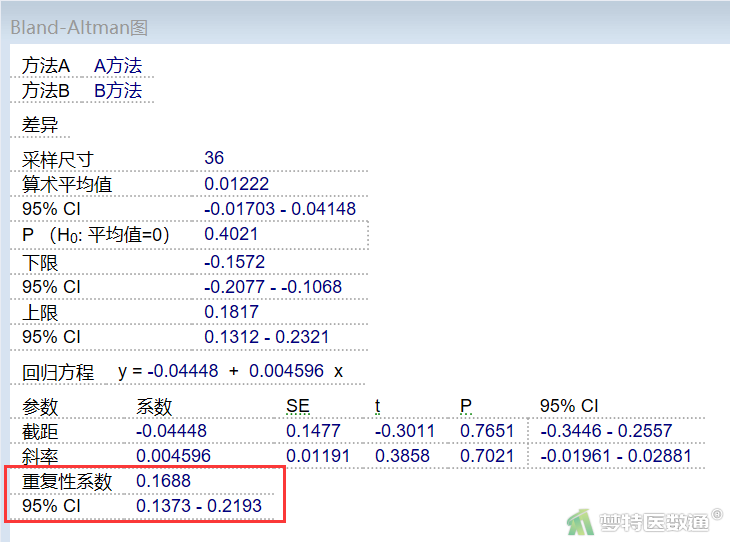
鼠标右击Bland-Altman图,选择“信息”,可得到重复系数(coefficient of repeatability, CR)来评价检测方法的可重复性(图11)。可见CR及其95%CI为0.1688 (0.1373~0.2193),均小于临床上可接受的临界值范围0.3,表明两种方法的可重复性较好。
综上,可认为A、B两种检测方法的结果一致性较好,可以互相替换。
四、结论
本研究采用Bland-Altman法判断A和B两种方法检测脑脊液标本中某指标(X)的含量结果是否一致。通过专业知识判断, A和B两种方法检测差值近似服从正态分布,差值D与均值A独立且散点分布均匀,差值的回归线与零刻度线平行,满足Bland-Altman法的使用条件。
结果显示,有1个点(2.78%)落在LoA之外,但并无点落在LoA的95%CI之外,LoA的95%CI均位于专业上允许的最大差异线之内。两种方法测量结果的的差异无统计学意义(P=0.4021)。Bland-Altman回归方程y =-0.04448+0.004596 x,方程总体截距和斜率的95%CI分别为(-0.3446~0.2557)和(-0.01961~0.02881),均包含0,P值均大于0.05,截距和斜率与0的差异无统计学意义,表明两种方法测量结果不存在比例差异。重复系数(CR)及其95%CI为0.1688 (0.1373~0.2193),均小于临床上可接受的临界值范围0.3。可认为两种方法测定结果一致性较好。
五、分析小技巧
(一) 适用条件
- 若原始数据不满足应用条件,可考虑进行数据转换,如对数转换,也可考虑通过改变纵轴的尺度,达到应用条件后再采用Bland-Altman法。
(二) 其他Bland-Altman图
- Bland-Altman图功能除了可绘制经典的Bland-Altman图外,还可绘制各种变体,其纵坐标可为两种方法的平均值、第一种方法或第二种方法的测量值、两种方法的几何平均值,X轴可以绘制差异、差异的百分比(%)及比率。
- 本案例为两种方法测量结果的一致性分析,Bland-Altman法还可分析两种方法多次测量结果的分析,以及多种方法测量结果的一致性分析。