连续变量的一致性评价ATE/LER区域法——SAS软件实现

关键词：SAS; 无金标准诊断实验; ATE/LER区域; 一致性检验

一、概述

随着医学诊疗技术的迅猛发展，针对同一领域范畴的新的诊断试验方法和项目不断被开发推广。因此急需便捷适宜的一致性评价方法，快速准确地评价两种方法或仪器诊断结果之间的一致性。ATE/LER区域是美国FDA推荐的用于评价一致性的指标，其主要原理是分析两种方法测量结果的总体吻合度，并用图形直观地加以反应，最后结合临床意义，评估两种测量方法的一致性。ATE/LER图形中各区域部分的划分需要临床专家和统计学专家共同做出判断，以制定临床界值。

二、图示解读

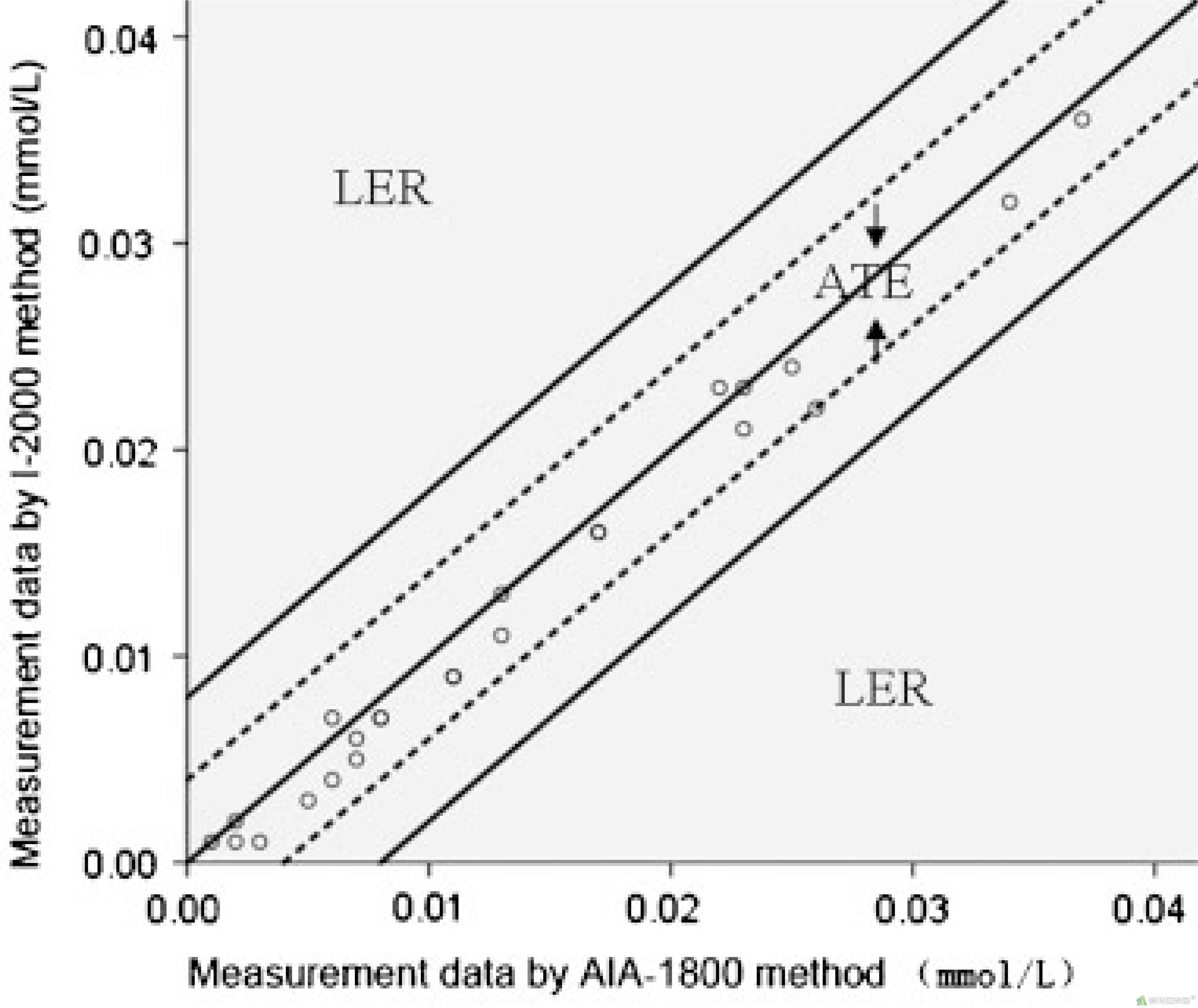
如图1(来自Journal of Clinical Laboratory Analysis, 2011;25(2):83-89.)所示，当两种检测方法完全一致时，散点均匀地分布在图中的对角线Y=X上。一般而言，散点围绕对角线上下波动。结合临床意义可将图形划分为3个区域：

• ATE区域，围绕Y=X附近的虚线范围内的条带区域，此区域内误差在临床应用中可以接受，就总体而言，观察对象落入ATE区域内应超过95%。
• LER区域，位于ATE两条实线区域外围的区域，它的划分确定了两种检测方法的差异界限，此区域内误差不可忽略，并且散点数必须为0。若有散点落入此区域，表示两种检测方法的一致性差，检测方法不得用于临床应用。
• 中间区域，位于ATE区域与LER区域之间的区域(外围实线和虚线之间)，此区域内误差在一定范围内可以接受，就总体而言，观察对象落入中间区域内不得超过5%。

只有同时满足三个区域的判定标准时，才可以认为两种方法一致性良好。

三、方法学实现

(一) 数据介绍

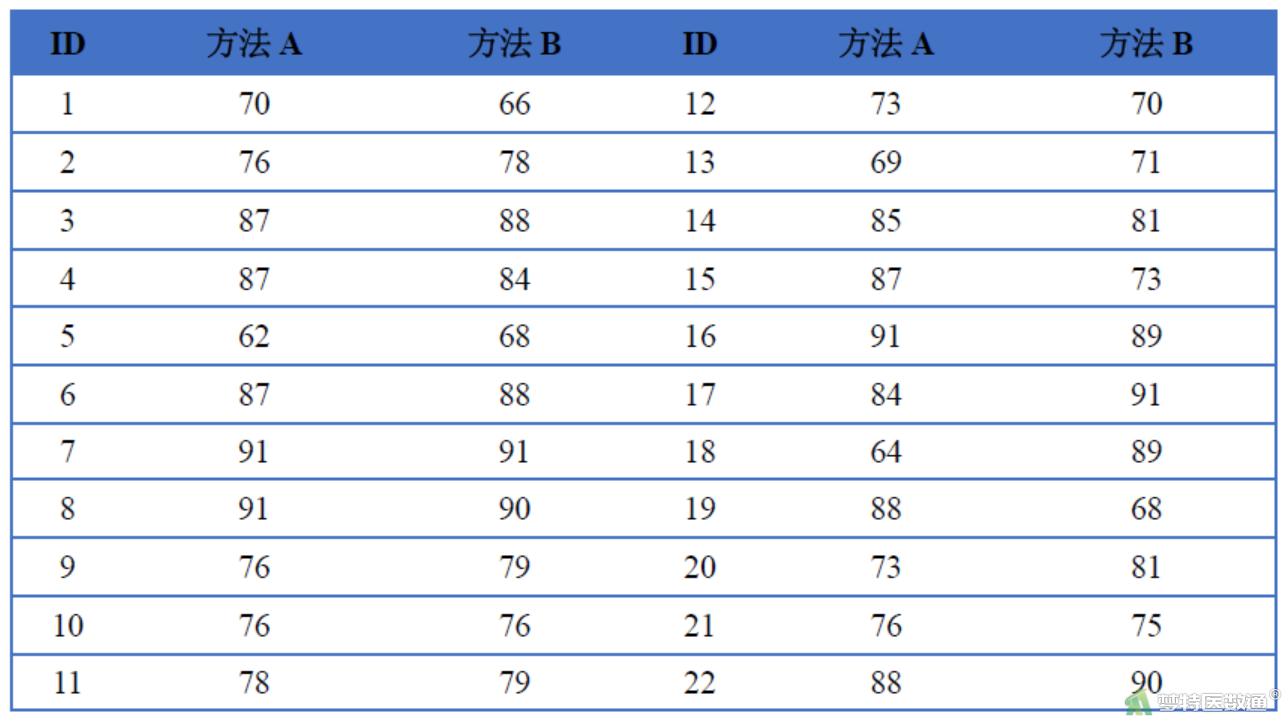
为比较两种方法检测血压的一致性，随机采集22位门诊健康志愿者的舒张压数据，如表1。

表1

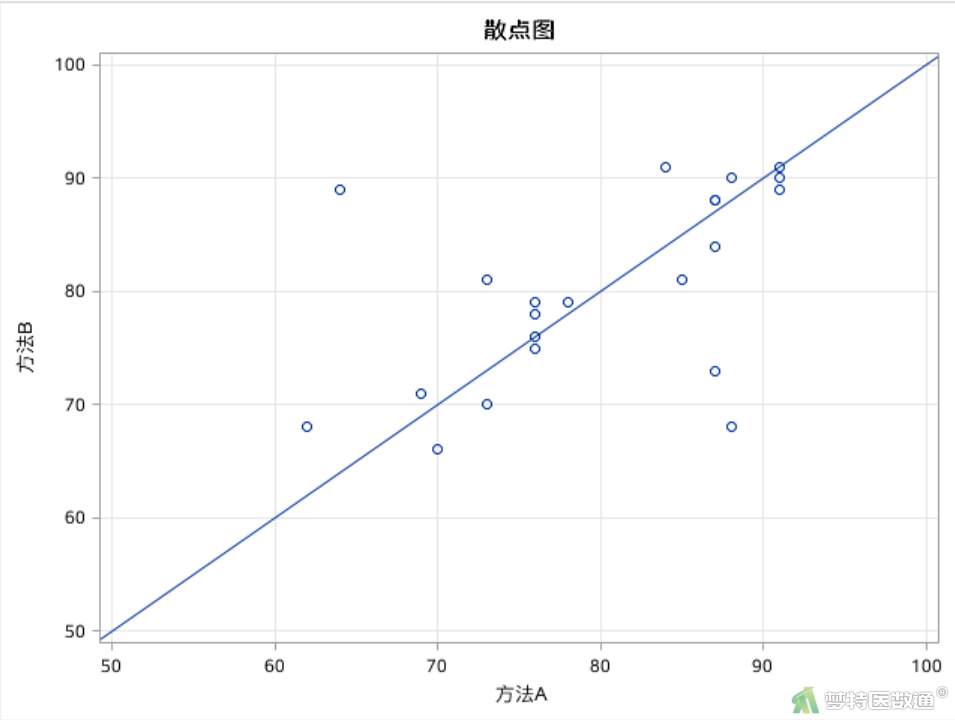
(二) 绘制散点图及Y=X的参考线

data example;
input a b;
label a="方法A" b="方法B";
cards;
70	66 
76	78
87	88
87	84
62	68
87	88
91	91
91	90
76	79
76	76
78	79
73	70
69	71
85	81
87	73
91	89
84	91
64	89
88	68
73	81
76	75
88	90
;
run;
proc sgplot data=example noautolegend;
  title "散点图";
  scatter x=a y=b;
  lineparm x=0 y=0 slope=1; /** intercept, slope **/
  xaxis values=(50 to 100 by 10) grid;
  yaxis values=(50 to 100 by 10) grid;
run;

(三) 确定ATE和LER区域

通过临床专家和统计学家共同讨论，确定ATE和LER区域的界限值以及相应95%CI的上限或下限。

假设根据临床专家的建议，ATE区域为±5 mmHg的偏差范围内，LER区域为±15mmHg的偏差范围外。这里的内外之说，主要区别于是内部面积还是外部面积，本案例数据及偏差范围均为模拟举例，谨记不可套用于临床实际。

(四) 估计各区域落点百分比及95%CI

通过Newcombe-Wilson得分法估计每个区域落点比例及其95%CI，并根据相关内容制定如表2所示统计学表格。

data example_1;
	set example;
	ATE1=a+5;
	ATE2=a-5;
	LER1=a+15;
	LER2=a-15;
	if b ge ATE2 and b le ATE1 then ZONE="ATE    ";
		else if b ge LER1 or b le LER2 then ZONE="LER";
		else ZONE="ATE-LER";
proc print;run;

proc freq data=example_1;
table zone/out=out;
run;

data out_1;
	set out;
	n=22;
	alpha=0.1;
	p=percent/100;
	q =1-p;
	z = probit(1-alpha/2);
	L = round((2*count+z**2 - z*sqrt(z**2 + 4*p*(n*q))) / (2*(n+z**2))*100,0.01);
	U = round((2*count+z**2 + z*sqrt(z**2 + 4*p*(n*q))) / (2*(n+z**2))*100,0.01);
proc print;run;

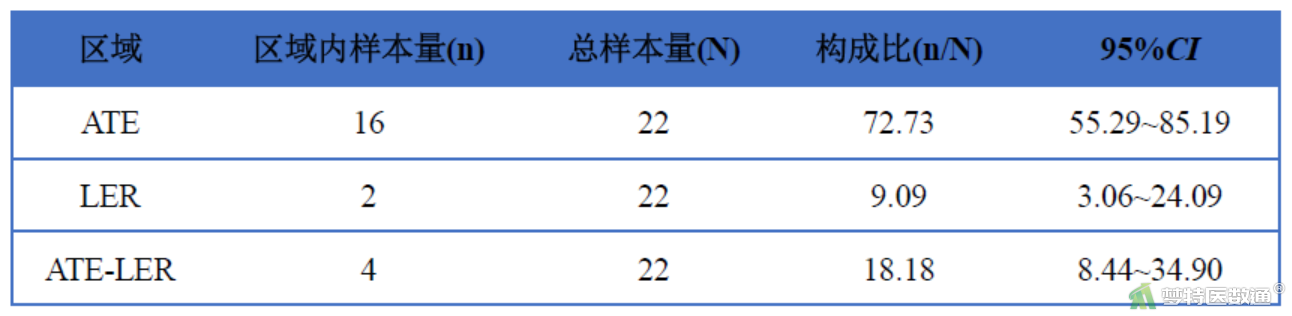
表2

95%CI计算公式如下：

\(\left[2 n p+z^{2} \pm \mathrm{z} \sqrt{\left(z^{2}+4 n p q\right)}\right] / 2\left(\mathrm{n}+z^{2}\right)\)

其中，n为样本量，p为落入ATE/LER区域的比例(以0.xx数据形式参与计算)，q为1-p，z为α=0.05单侧值，即1.645。

(五) 绘制ATE和LER区域图

proc sgplot data=example noautolegend;
  title "Graph with Diagonal Line";
  scatter x=a y=b;
  lineparm x=0 y=0 slope=1; /** intercept, slope **/
  lineparm x=0 y=5 slope=1; /** intercept, slope **/
  lineparm x=5 y=0 slope=1; /** intercept, slope **/
  lineparm x=0 y=15 slope=1; /** intercept, slope **/
  lineparm x=15 y=0 slope=1; /** intercept, slope **/
  xaxis values=(50 to 100 by 10) grid;
  yaxis values=(50 to 100 by 10) grid;
run;

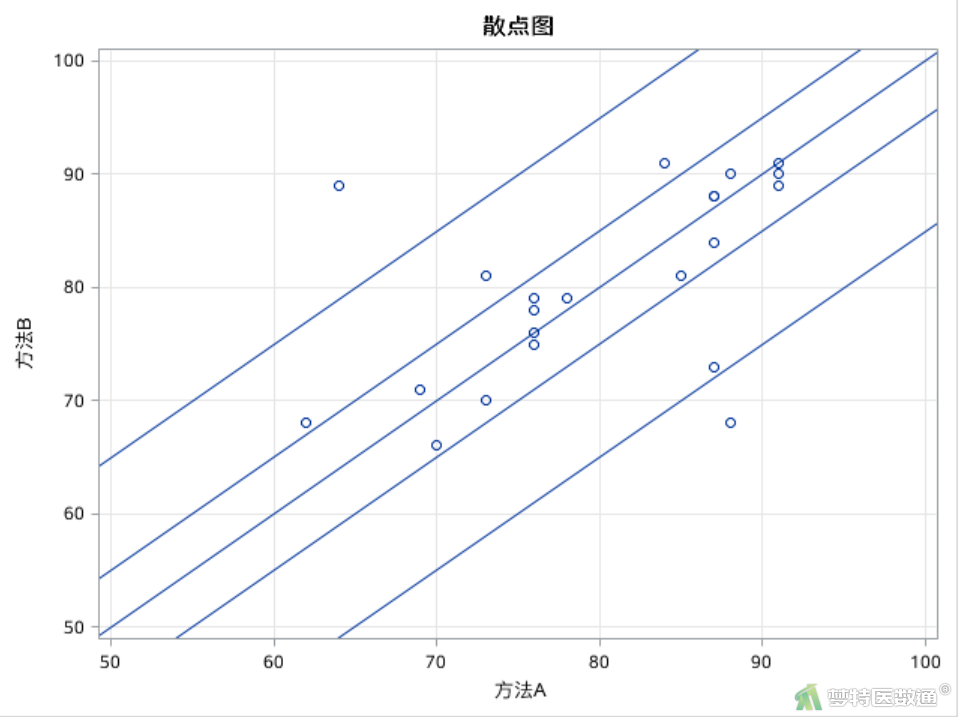
四、结果解读

根据表2可知，A、B两种方法测得舒张压数值落在ATE区域的比例为72.73% (95%CI：55.29%~85.19%) 远低于要求的95%，且落在LER区域的比例为9.09% (95%CI：3.06%~24.09%) 也远高于要求的0%。综合考虑，两种方法测量舒张压的一致性较差。