无金标准的诊断试验研究——概述

关键词：诊断试验; 诊断试验评价; 无金标准; 不完善的金标准

一、分类资料的一致性评价

如果诊断结果是二分类资料常使用配对卡方检验或Cohen's Kappa值评价一致性；

如果诊断结果是有序多分类资料常使用Kendall's tau-b相关分析、Kendall's W协同系数、加权Kappa值或组内相关系数(ICC)评价一致性；

如果诊断结果是无序多分类资料常使用Cohen's Kappa值评价一致性。

(一) 配对卡方检验

配对卡方检验常用于二分类诊断结果的一致性评价。配对卡方(χ²)检验也称McNemar检验，是根据四格表中假阳性数(b)和假阴性数(c)计算统计量，并行统计学推断而得出的结果(配对四格表资料的χ²检验——理论介绍)。

该方法一般用于样本含量不太大的资料，因为该法仅考虑了两种检测方法结果不一致的两种情况(b和c)，而未考虑样本含量n和两种方法结果一致的两种情况(a和d)。所以，当n很大且a与d的数值很大(即两法的一致率较高)，b和c的数值相对较小时，即便是检测结果有统计学意义，其实际意义往往也不大。

(二) Cohen's Kappa一致性检验

Cohen's Kappa值可用于二分类、无序多分类诊断结果的一致性评价。Cohen's Kappa值考虑了机遇因素对一致性的影响，取值范围为-1~1。其常用的判断说明见图2。

计算公式为：

\(K=\frac{n(a+d)-\left(r_{1} c_{1}+r_{2} c_{2}\right)}{n^{2}-\left(r_{1} c_{1}+r_{2} c_{2}\right)}\)

(三) Kendall's tau-b相关分析

Kendall's tau-b相关分析常用于有序多分类诊断结果的一致性评价。Kendall's tau-b系数是一种非参数方法，通过将两组测量值分别排序并进行秩次转换后检查两组数值的排序是否一致。Kendall's tau-b相关系数的取值范围为-1~1，相关系数＜0表示两变量负相关，＞0表示正相关，＝0表示两变量相互独立。相关系数的绝对值越大，表示两变量间的相关程度越密切；相关系数越接近于0，表示相关越不密切。

(四) 加权Kappa值

加权Kappa(weighted Kappa)值可用于有序多分类诊断结果的一致性评价。加权Kappa系数是Cohen's Kappa系数的推广，是用加权的方法对两个评价结果进行量化所得。加权Kappa系数取值范围为-1~1。其常用的判断说明见图3。

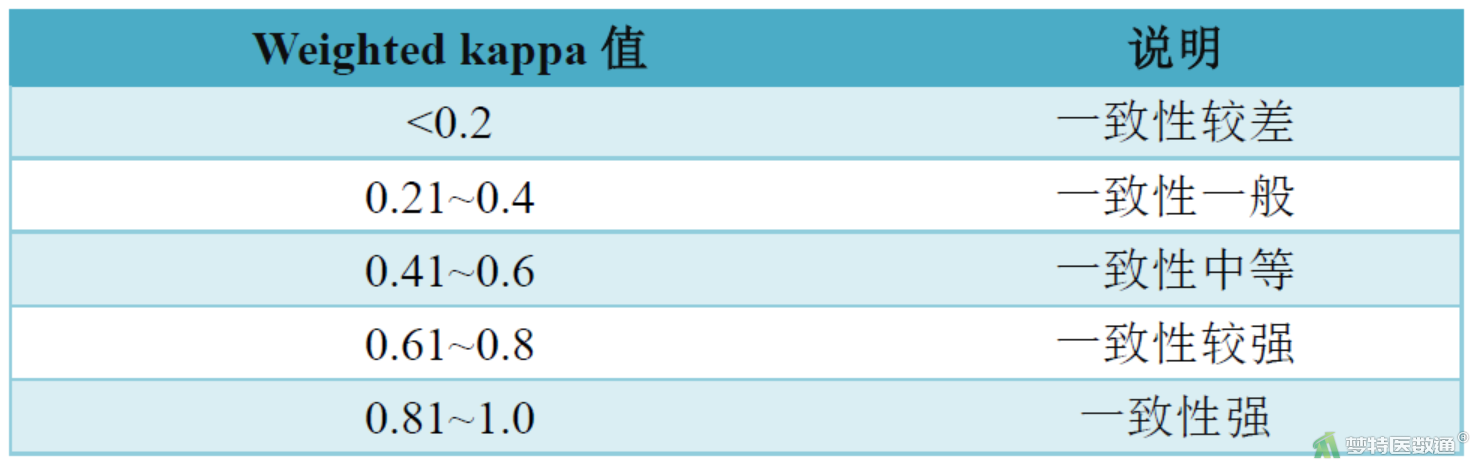
(五) Kendall-W协调系数

Kendall-W协调系数也称Kendall-W一致性系数，可用于有序多分类诊断结果的一致性评价。Kendall协调系数W检验是一种非参数检验方法，其基本原理是由b个诊断方法(评价员)对k个被诊断对象进行评分，然后检验b个诊断方法的评价结果是否具有一致性。Kendall-W协调系数的范围从0 (完全不一致)~ 1(完全一致)。其判断说明可参照加权Kappa值(图3)。

计算公式为：\(W=\frac{12 \sum_{j=1}^{K} R_{j}^{2}-3 b^{2} k(k+1)^{2}}{b^{2} k\left(k^{2}-1\right)}\)

其中，b是诊断方法个数、k是被诊断对象个数，R_j是分配给第j个观察对象的秩次合。

二、计量资料的一致性评价

(一) 配对t检验

配对t检验的实质是在将配对数据求差值后，检测差值的均数是否与0有统计学差异，以此判断两组数据差异是否有统计学意义。在诊断试验研究中，两种检测方法之间的数值差异有无统计学意义，反映了两种方法检测结果是否有差异。当P<0.05可认为两种方法检测结果不一致，反之，P≥0.05可认为两种方法检测结果一致。

配对t检验统计量可按如下公式计算：

\(t=\frac{\bar{d}-\mu_{d}}{S_{\bar{d}}}=\frac{\bar{d}-0}{S_{d} / \sqrt{n}}=\frac{\bar{d}}{S_{d} / \sqrt{n}}, \quad v=n-1\)

其中，\(\bar{d}\)为差值的样本均数，S_d为差值的标准差，\(S_{\bar{d}}\)为差值样本均数的标准误，n为对子数。

但配对t检验用于诊断试验一致性评价存在固有缺陷：

• 配对t检验不能兼顾每一个被测对子的差异，而是根据总体均值对测量结果是否一致作出评价，其测量本质是对总体“差异”的检验，而非“一致”性评估。故配对t检验用于一致性的评价，结果往往欠准确。
• 在样本量较大的情况下，配对t检验很容易出现P<0.05的情况，据此得出的两诊断试验结果不一致往往不具备实际意义。
• 配对t检验用于诊断试验一致性判定，得出的结论是“有”或“无”一致性，难以说明一致性程度。

(二) Pearson相关分析

Pearson相关分析通过计算两连续性变量之间的相关系数r的大小和方向判断两变量之间的关联大小和方向，通过检验相关系数r是否来自ρ=0的总体判断相关性是否有统计学意义。在诊断试验研究中，两种检测方法之间的相关系数r越大间接反映了检测结果的一致性越高，并通过P是否小于0.05判断一致性是否有统计学意义。Pearson相关系数范围为-1~1。其常用的判断说明如下：

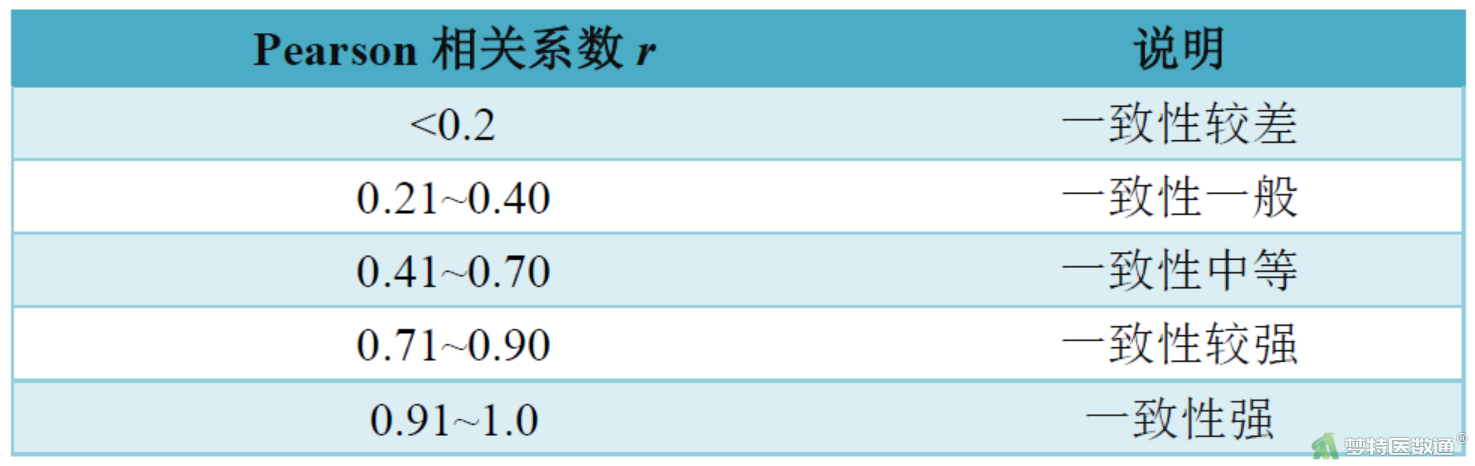
需要注意的是，Pearson相关系数r其本质反应的是两者之间的相关，而非一致性。因此对系统误差并不敏感，对测量值增加固定的数值后，其相关系数并不会发生改变。

(三) 组内相关系数

组内相关系数(ICC)是两种诊断方法测量结果的变异占总变异的比例，同时考虑了系统误差与随机误差的影响。ICC不仅适用于计量资料，也适用于有序分类变量的一致性评价。

计算公式为：

\(I C C=\frac{M S_{\text {区组}}-M S_{\text {误差}}}{M S_{\text {区组}}+(k-1) M S_{\text {误差}}+\frac{k\left(M S_{\text {处理}}-M S_{\text {误差}}\right)}{n}}\)

其中，MS_区组为随机区组(被观察对象)间的均方(方差)，MS_误差为误差的均方，MS_处理为处理组(检测方法)的均方。k为重复次数(测量方法的数量)，n为被观察对象的例数。ICC介于0~1之间，0表示完全不一致，1表示完全一致。其推荐的判断说明如下：

ICC评价一致性可以同时兼顾系统误差和随机误差，与配对t检验和Pearson相关分析相比，具备其独特的优势。但当样本量较小时，ICC系数容易被低估。

(四) Bland-Altman法

Bland-Altman法的原理是根据两种诊断方法的测量结果，计算出95%一致性界限(95% limits of agreement, 95% LoA)，及1.96倍标准差，并用图形直观的呈现结果(图6来自广西师范大学学报(自然科学版), 2022, 40(1): 125-138.)。最后结合临床实际允许的最大误差，得出两种方法(或两位评价者)是否具有一致性的结论。

图中横实线是两种测量方法差值的均值线，上下的虚线是差值的±1.96倍标准差。因此Bland-Altman法绘制的图形，又称D-A图，D为两种诊断方法测量的差值，A为两种诊断方法测量的均值。Bland-Altman法评价一致性既考虑了随机误差也考虑了系统误差，同时可以结合专业意义进行判断，具有独特的优势。

• 当D与A独立时，散点一般均匀的分布在条带内。此时，95%一致性界限可作为评价一致性的指标，如果散点都在标准差线内均匀分布，且均值线接近0值，说明两测量结果较为接近，反之则两种方法一致性欠佳。
• 当D与A不独立时，如随着测量均值(横坐标)的增大，散点的分布呈现向右的漏斗形，则说明两种测量方法在对较大数据的测量时差异较大；反之亦然。此时，不能简单的计算一致性界限，需要根据Bradley-Blackwood检验结果判断两种测量数据的一致性。

(五) ATE/LER区域

ATE/LER区域是美国FDA推荐用于评价一致性的指标，其主要原理是分析两种方法测量结果的总体吻合度，并用图形直观地加以反应，最后结合临床意义，评估两种测量方法的一致性。ATE/LER图形中各区域部分的划分需要临床专家和统计学专家共同做出判断，以制定临床界值。

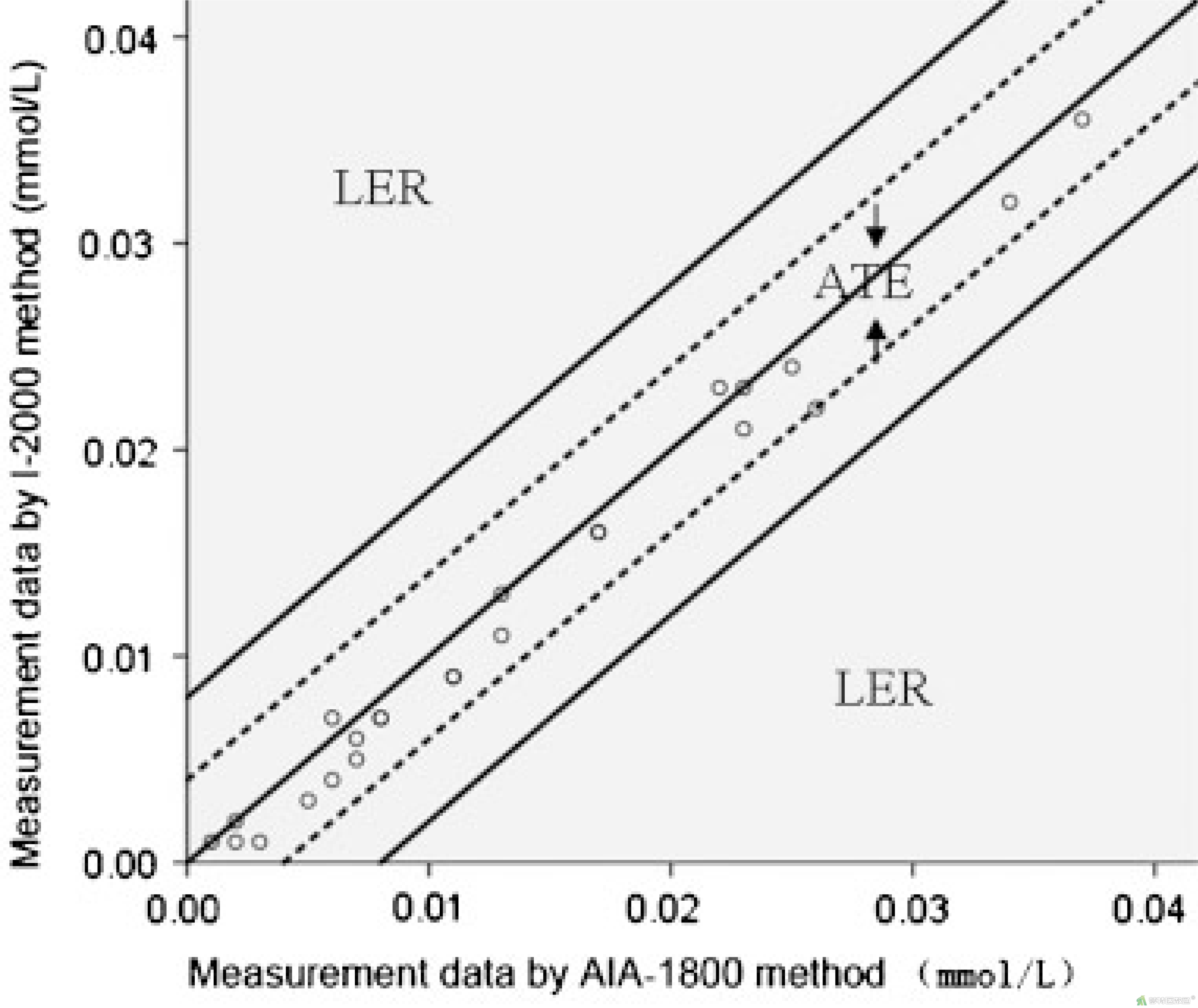
如图7(来自Journal of Clinical Laboratory Analysis, 2011;25(2):83-89.)所示，当两种检测方法完全一致时，散点均匀地分布在图中的对角线Y=X上。一般而言，散点围绕对角线上下波动。结合临床意义可将图形划分为三个区域：

• ATE区域，围绕Y=X附近的虚线范围内的条带区域，此区域内误差在临床应用中可以接受，就总体而言，观察对象落入ATE区域内应超过95%。
• LER区域，位于ATE两条实线区域外围的区域，它的划分确定了两种检测方法的差异界限，此区域内误差不可忽略，并且散点数必须为0。若有散点落入此区域，表示两种检测方法的一致性差，检测方法不得用于临床应用。
• 中间区域，位于ATE区域与LER区域之间的区域(外围实线和虚线之间)，此区域内误差在一定范围内可以接受，就总体而言，观察对象落入中间区域内不得超过5%。

只有同时满足三个区域的判定标准时，此时才可以认为两种方法一致性良好。

(六) Deming回归

Deming回归又称戴明回归，可用于检验两种诊断方法检测的计量资料是否一致。普通的线性回归(最小二乘回归)假设只有Y的测量值与随机误差相关，而Deming回归则考虑了两种方法(X和Y)的测量误差。为了尽量消除两种检测方法的随机误差，Deming回归需要对每个样本进行两次平行测定，若是只有一次测定则需要输入已经建立的变异系数。

通过对拟合的回归模型进行判断，若截距的95%置信区间包含0、斜率的95%置信区间包含1，且残差围绕参考线对称分布，则表明两种方法检测结果一致。

(七) Passing-Bablok回归

Passing-Bablok回归是一种非参数检验方法，该方法不要求样本分布和测量误差满足特别的假设，比较适合于数据中存在异常值时。其基本思想是任意取两点确定直线，得到斜率，多次反复后得到多个斜率，然后计算斜率的中位数。需要注意的是该方法需要两种检测的测量值高度相关时才有效，使用过程中往往结合Bland-Altman图一起评估一致性。

三、其他方法

除了上面介绍的一些常用的关于分类资料和计量资料一致性评价的方法外，还有一些使用较少的无金标准诊断情况下评价诊断试验准确性的统计学方法。

(一)缺失数据填补法

适用于部分受试者没有金标准或参考标准的情况。根据数据缺失机制(如完全随机缺失、随机缺失、非随机缺失)，采用合适的填补方法进行数据填补，然后按照有金标准的诊断试验研究进行分析。

(二)偏倚校正法

如果已知金标准的灵敏度(S_e)和特异度(S_p)，在诊断试验与金标准条件独立的假设下，可以对诊断试验的灵敏度和特异度进行校正。

(三)差异化验证与分析

差异化验证(Differential verification)是指对部分无金标准诊断结果的受试者采用其他可用的参考标准对疾病状态进行确证。差异化分析(Discrepant analysis)是指对诊断试验与金标准结果不一致的受试者，采用另一种标准方法来确证疾病状态，并更新诊断试验的四格表后进行分析。

(四)潜在类别/剖面分析

当受试者的疾病状态是无法直接观测的潜在变量，可通过联合同一受试者的多个可直接观测指标构建潜在分类模型，以利用构建的潜在类别变量作为参考标准，计算诊断试验的准确性评价指标。

(五)贝叶斯评价法

利用目标诊断人群中的患病率及参考标准的灵敏度、特异度的先验信息，通过似然函数对参数的先验分布进行调整，从而对需要评估的诊断试验的灵敏度和特异度进行估计。

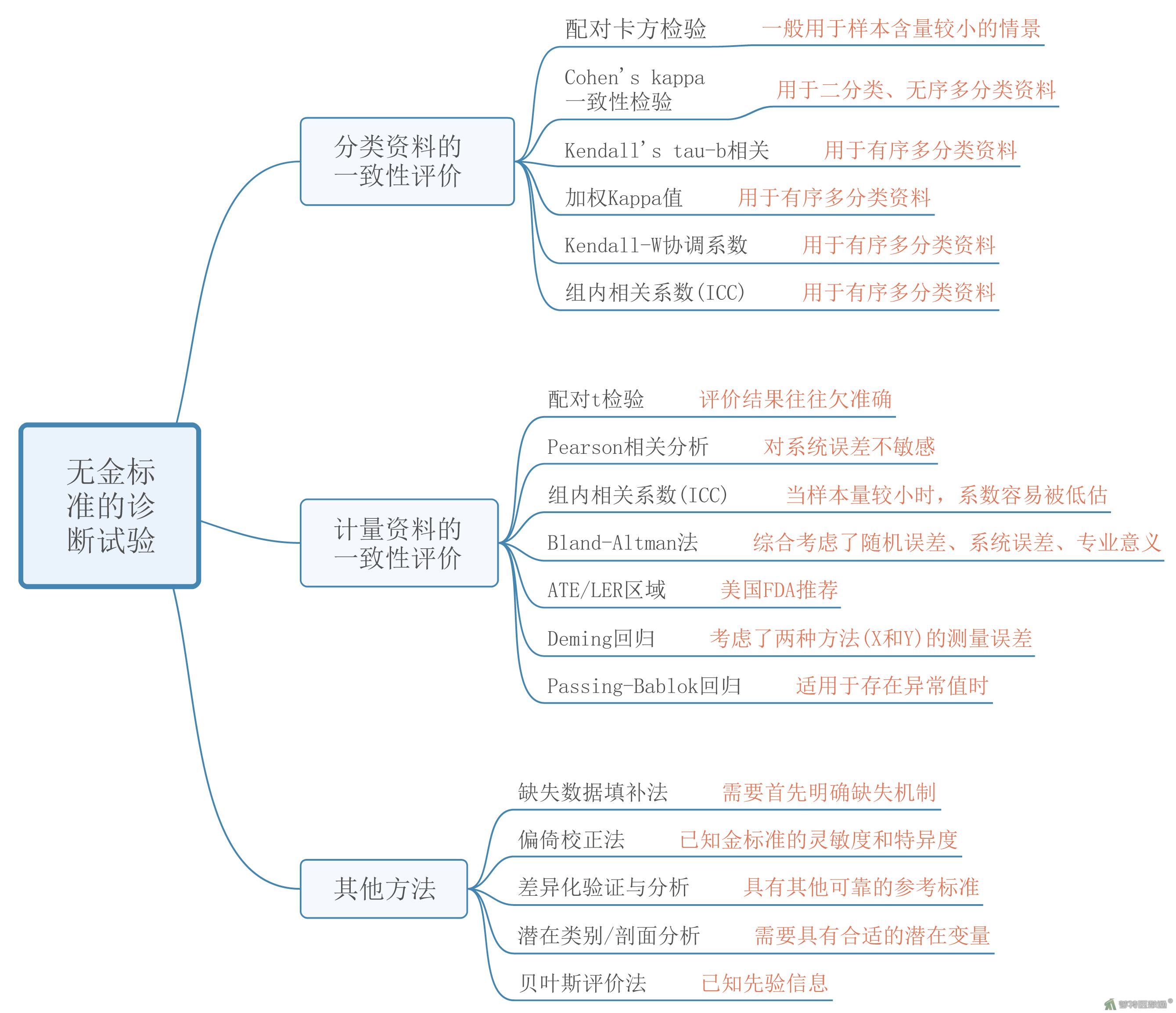
最后，图8汇总了本文提到了各种方法及主要特征。