无金标准的诊断试验研究——配对t检验和Pearson相关

关键词：无金标准诊断试验；连续型指标；配对t检验；Pearson相关系数；一致性分析

一、案例介绍

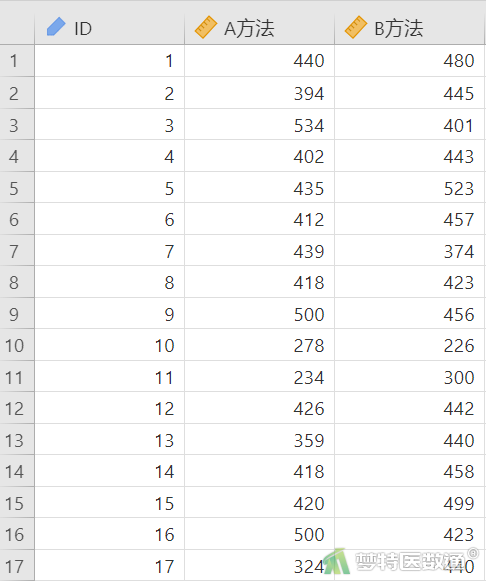
为检测血液中某肿瘤指标(X)的含量，分别使用A、B两种方法检测17例该肿瘤患者血液中该指标的含量，试评价两种检测方法的一致性。数据见图1，本文案例可从“附件下载”处下载。

二、问题分析以及软件操作

(一) 问题分析

配对t检验的实质是在将配对数据求差值后，检测差值的均数是否与0有统计学差异，以此判断两组数据差异是否有统计学意义，相关理论见“配对样本t检验(Paired Samples t-test)——理论介绍”。在诊断试验研究中，两种检测方法之间的数值差异有无统计学意义，反映了两种方法检测结果是否有差异。当P<0.05可认为两种方法检测结果不一致，反之，P≥0.05可认为两种方法检测结果一致。但配对t检验用于诊断试验一致性判定，得出的结论是“有”或“无”一致性，难以说明一致性程度。

Pearson相关分析通过计算两连续性变量之间的相关系数r的大小和方向判断两变量之间的关联大小和方向，通过检验相关系数r是否来自ρ=0的总体判断相关性是否有统计学意义[Pearson相关性分析(Pearson Correlation Analysis)——理论介绍]。在诊断试验研究中，两种检测方法之间的相关系数r越大表明检测结果的一致性越高，并通过P是否小于0.05判断一致性是否有统计学意义。当0.9<|r|<1，为高度相关；当0.7<|r|<0.9，为强相关；0.4<|r|<0.7，为中度相关；0.2<|r|<0.4，为弱相关性；0<|r|<0.2，为极弱相关或无相关性。

(二) 软件操作

可参考配对样本t检验(Paired Samples t-test)——SPSS软件实现以及Pearson相关性分析(Pearson Correlation Analysis)——SPSS软件实现，或网站相关软件操作。本文使用jamovi软件进行分析。

三、配对t检验结果解读

(一) 统计描述

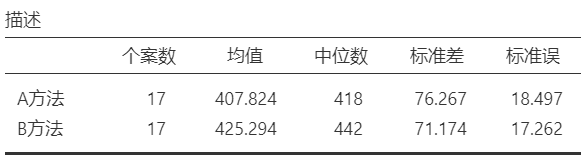
图2是两组变量的统计描述结果，可见A、B方法检测结果分别为407.824±76.267、425.294±71.174。从均值看两种方法检测结果可能存在差异，但还需要依据统计学检验的结果进行判断。

(二) 统计学推断

图3是配对样本t检验的结果，显示使用A方法检测该肿瘤指标 (X)比使用B方法检测数值低17.471，95%CI为-52.775～17.834，差异无统计学意义(t=-1.049，P=0.310)。

四、Pearson相关分析结果解读

(一) 线性关系分析

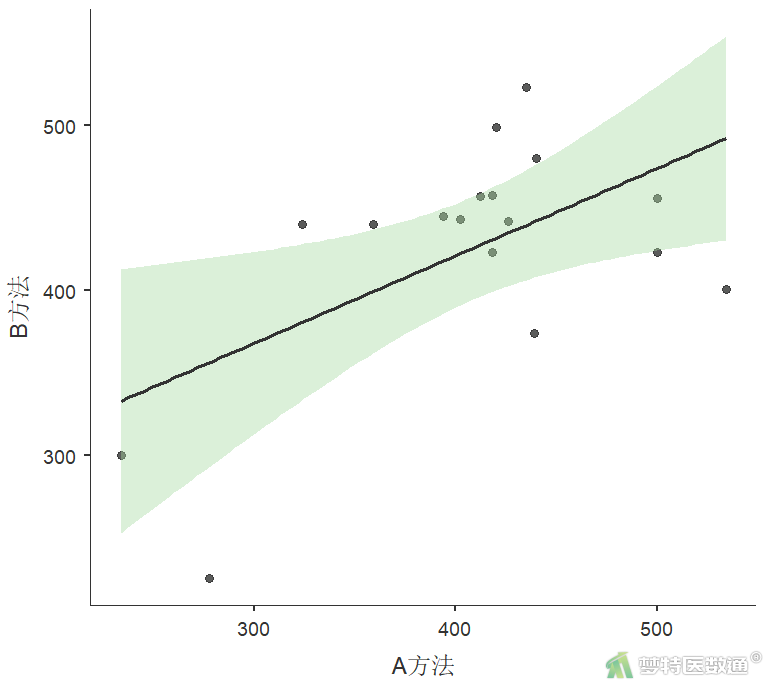
首先绘制散点图描述A、B方法之间的线性关系。图4为方法A和B的散点图，散点大致呈一条直线，说明存在线性关系。

(二) 统计学推断

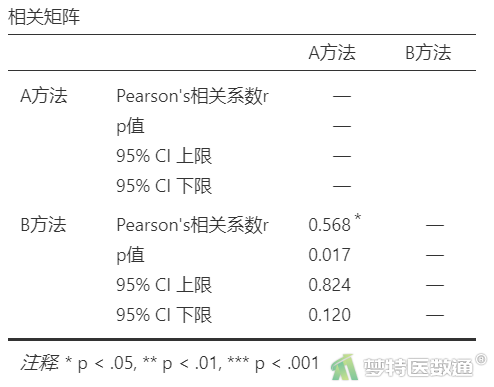
图5的“相关性”分析结果显示，两组Pearson相关系数r =0.568，P=0.017。可知该肿瘤指标的检测方法A和B之间线性相关性为中度水平。表明A、B两种检测方法检测结果的一致性一般。

四、知识小贴士

(一) 配对样本t检验的缺陷

• 配对t检验不能兼顾每一个被测对子的差异，而是根据总体均值对测量结果是否一致作出评价，其测量本质是对总体“差异”的检验，而非“一致”。故配对t检验用于一致性的评价结果往往欠准确。
• 在样本量较大的情况下，配对t检验很容易出现P<0.05的情况，据此认为两诊断试验结果不一致往往不具备实际意义。
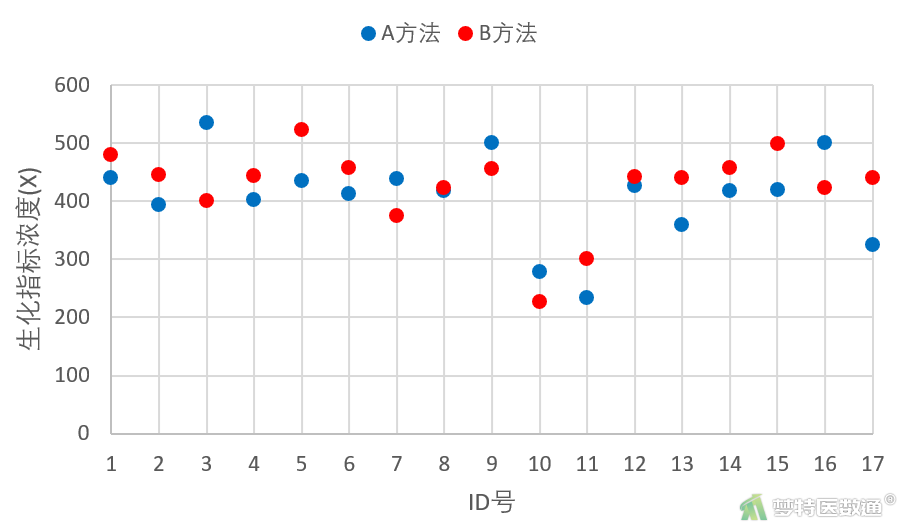
• 配对t检验用于诊断试验一致性判定，得出的结论是“有”或“无”一致性，难以说明一致性程度。这主要是因为配对样本t检验比较的是两种方法检测结果的“平均”效应，换言之，尽管单个样本中有A比B结果高和B比A结果高的各种情况，但是只要两组的均数相差不大，就会得出差异无统计学意义的结果(图6为本案例两组数据的比较情况)。而辅助使用Pearson相关分析可进一步补充说明一致性的程度。

(二) Pearson相关分析的缺陷

Pearson相关系数r其本质反应的是两者之间的相关，而非一致性。因此对系统误差并不敏感，对测量值增加固定的数值后，其相关系数并不会发生改变。