配对样本t检验(Paired Samples t-test)——SPSS软件实现

关键词：SPSS; t检验; 配对样本t检验; 配对t检验; 成对t检验;关联样本t检验; 差值正态性

一、案例介绍

为检测肌肉组织中某生化指标(X)的含量，分别使用A、B两种方法检测17只小白鼠肌肉组织中该生化指标(X)的含量，试问两种方法检测的结果是否有差异？

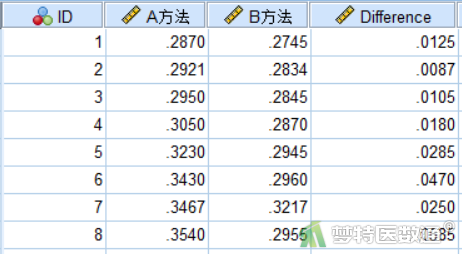
创建数值型变量“A方法”和“B方法”，测量尺度设为“标度”，分别表示用A方法和B方法检测出的小白鼠肌肉组织中该生化指标(X)的含量。部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是比较两种检测方法对同一批样本检测的结果是否存在差异，由于检测的指标是计量资料，因此可以使用配对样本t检验。但需要满足5个条件：

条件1：观察变量为连续变量。本研究中的生化指标(X)含量为连续变量，该条件满足。

条件2：观察变量为配对设计。本研究中，两组数据均是对同一批研究对象测量所得，因此属于配对样本。该条件满足。

条件3：观察变量可分为2组，本研究中分为A方法和B方法两组，该条件满足。

条件4：观察变量不存在显著的异常值，该条件需要通过软件分析后判断。

条件5：两个配对组别间观察变量的差值服从正态(或近似正态)分布，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件4判断(异常值判断)

配对样本t检验时，需要分别考察每一组的异常值情况。

(1) 软件操作

① 选择“分析”—“描述统计”—“探索”(图2)。

② 在“探索”对话框中将观察变量“A方法”和“B方法”均选入右侧“因变量列表”框，点击“确定”(图3)即可得到异常值判断结果。

(2) 结果解读

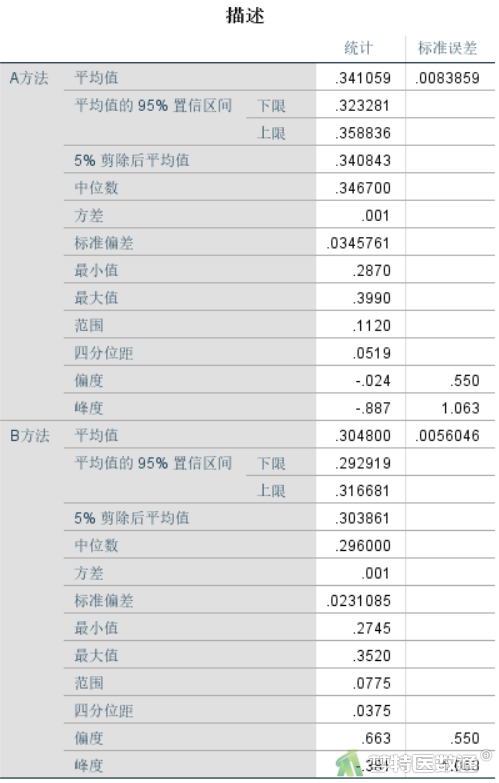
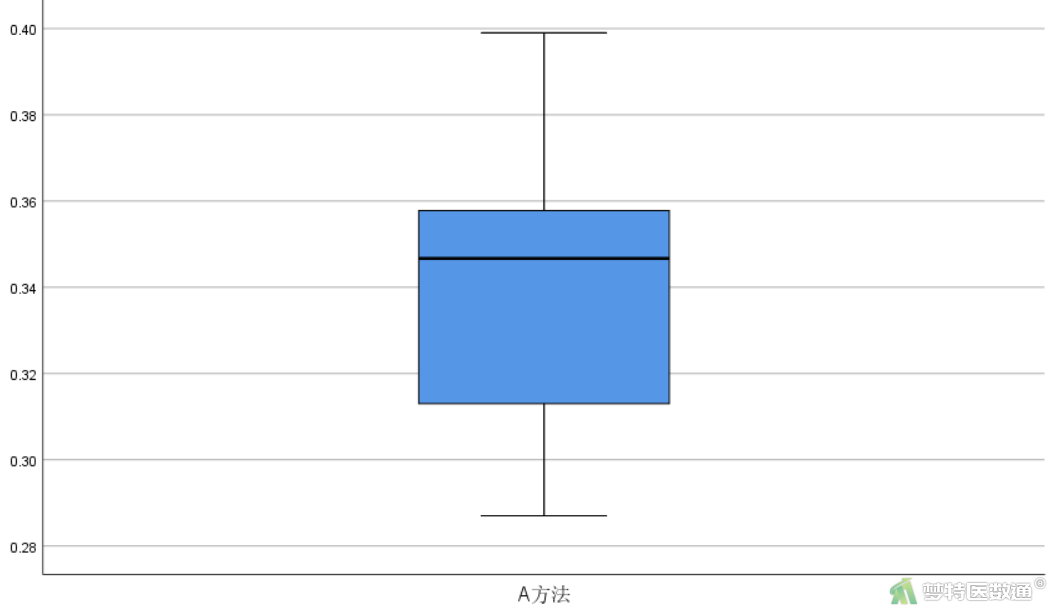
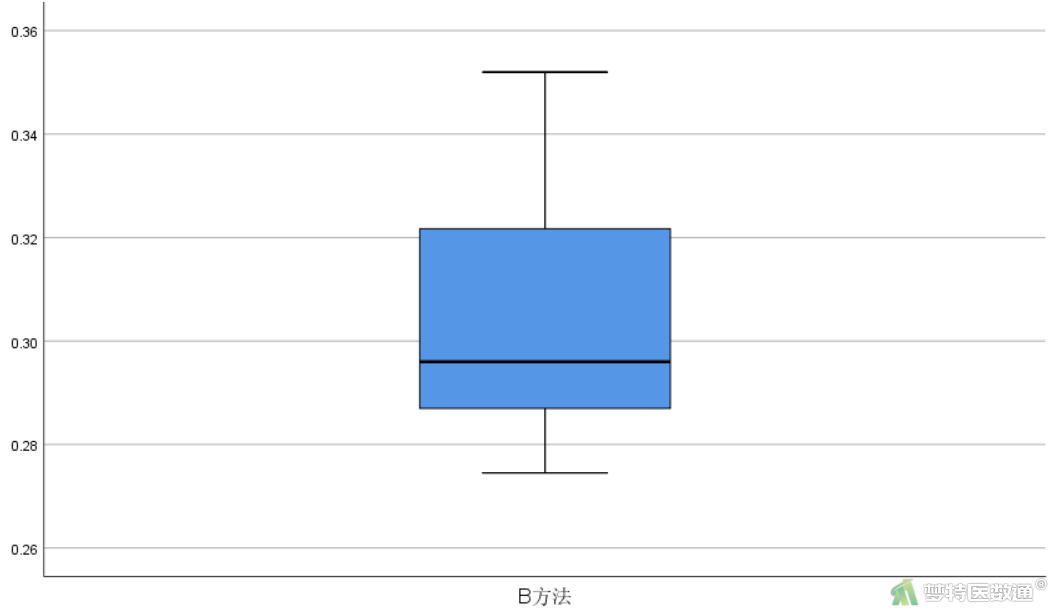
异常值判断结果如图4和图5所示。图4是对该观察变量基本情况的描述，列出了观察变量的最小值和最大值分别为0.27和0.40，尚无专业依据为异常值；此外，图5-1和图5-2分别为A、B两种方法检测数据的箱线图，也未提示任何异常值。综上，本案例未发现需要处理的异常值，满足条件4。

2. 条件5判断(正态性检验)

配对样本t检验时，需要考察两个配对组别间观测变量差值的正态性情况。所以正态性检验前先计算配对组别观察变量的差值。步骤如下：

(1) 软件操作

① 在主界面点击“转换”—“计算变量”(图6)。

② 出现“计算变量”对话框，在该对话框左侧的“目标变量”录入框中输入新创建变量的名称，此处命名为“Difference”。将变量“A方法”选入右侧“数字表达式”录入框中，然后点击下方的减号“-”，再将变量“B方法”选入“数字表达式”录入框中，点击“确定”(图7)。

③ 在“数据视图”和“变量视图”中均可看到新生成的变量“Difference”，“数据视图”中新变量显示在已有变量的最右侧，如图8所示。

接下来对表示两组差值的变量“Difference”进行正态性检验，步骤如下：

④ 选择“分析”—“描述统计”—“探索”。

⑤ 在“探索”对话框中将新生成的变量“Difference”选入右侧“因变量列表”框(图9)。

⑥ 在“图”子对话框中勾选“含检验的正态图”，取消勾选“茎叶图”，其他不变，如图10所示，点击“继续”，回到“探索”对话框，点击“确定”。

(2) 结果解读

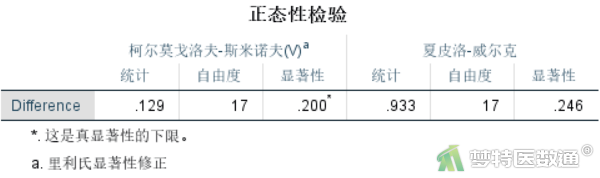
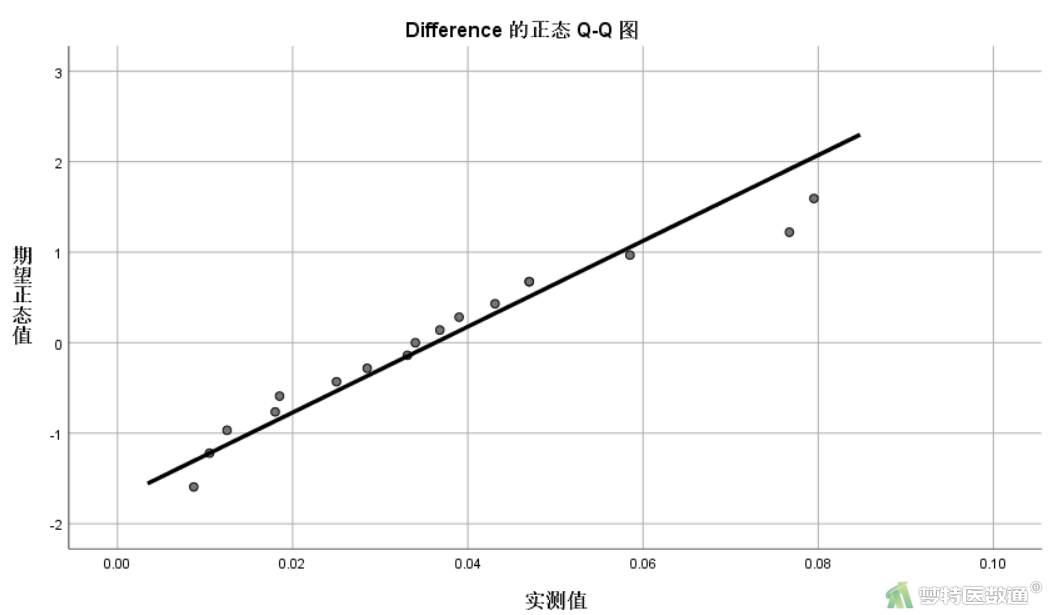
正态性检验的结果如图11和图12所示。图11显示了两种正态性检验的结果，柯尔莫哥洛夫-斯米诺夫，K-S检验和夏皮罗-威尔克正态性，S-W检验。K-S检验适用于大样本资料，本案查看S-W检验结果，结果显示P=0.246>0.1，提示数据满足正态性条件；图12的Q-Q图上散点基本围绕对角线分布，也提示数据呈正态分布。综上，本案例满足条件5。关于正态性检验的注意事项详见推文(医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现)。

(二) 统计描述及推断

1. 软件操作

① 选择“分析”—“比较平均值”—“成对样本T检验” (图13)。

② 在“成对样本T检验”对话框中将观察变量“A方法”和“B方法”分别选入右侧“变量1”和“变量2”处，点击“确定”(图14)。

2. 结果解读

(1) 统计描述

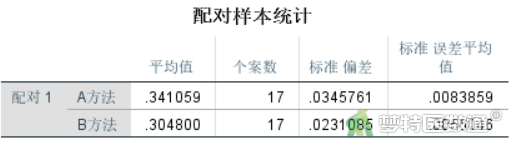
图15“配对样本统计”是两组变量的统计描述结果，可见A方法和B方法检测的两组“个案数”均为17， A方法检测的生化指标(X)的“平均值”是0.34，“标准偏差”是0.03，“标准误差平均值”是0.01。B方法检测的“平均值”是0.30，“标准偏差”是0.02，“标准误差平均值”是0.01。从均值看两种治疗方法检测结果可能存在差异，但还需要依据统计学检验的结果进行判断。

(2) 统计学推断

图17是配对样本t检验的结果，显示了配对样本差值的“平均值”、“标准偏差”、“标准误差平均值”及“差值95%置信区间的上限和下限”、统计量“t”、“自由度”、“Sig.(双尾)”。可知使用A方法检测该生化指标(X)比使用B方法检测数值高了0.04，95%CI为0.03~0.05，差异有统计学意义(t=7.085，P<0.001)。

(三) 相关性分析

图16“配对样本相关性”是配对样本相关性检验的结果，相关系数r=0.804，P<0.001，提示两组数据之间存在相关性。表明A、B两种方法之间的差异具有较好的稳定性。

四、结论

本研究采用配对样本t检验判断A、B两种方法检测肌肉组织中生化指标(X)的含量是否有差异。通过专业知识判断，数据不存在需要删除的异常值；通过绘制Q-Q图和Shapiro-Wilk检验，提示两组数据差值满足正态分布。

结果显示，A、B方法检测肌肉组织中生化指标(X)的含量分别为0.34±0.03和0.30±0.02，A方法平均值比B方法高0.04(95%CI：0.03~0.05)，差异有统计学意义(t=7.085，P<0.001)。两组Pearson相关系数r = 0.804，P < 0.001；表明A、B两种方法之间的差异具有较好的稳定性。因此，本案例分析表明，使用A方法检测肌肉组织中生化指标(X)的含量通常会比B方法检测结果值要高。

五、知识小贴士

(一) 配对设计

临床研究过程中常见的两组配对设计包括：

• 同一组研究对象身体不同部位配对，如癌组织与癌旁组织某种基因的表达、左手和右手的血压比较。
• 条件配对，如在同一窝老鼠中选择性别和体重相同的2只作为一个对子，组成多个这样的对子；再将每个对子中的2只老鼠随机分配到2个处理组中去，然后比较两种处理方法的效果。
• 同一批标本不同检测方法配对，如同一批血液，被分成2份，分别用两种方法检测某种生化指标的含量(本案例属于该种类型)。
• 还有一类特殊的研究设计，同一组研究对象干预前后配对，如同一组病人使用降血糖药物前后空腹血糖值的比较。对于这类设计，尽管可使用配对样本t检验进行数据分析，但严格来说并不属于配对设计，而是属于干预前后的重复测量设计。

(二) 相关性分析

相关性的计算是为了验证配对数据的一致性，可以说明研究因素作用的稳定性或一致性，可能存在四种情况。

• 相关性检验与配对t检验的P值均<0.05，说明数据一致性较好，差异有统计学意义，而且差异的产生就是研究因素作用的结果。
• 相关性检验P>0.05，配对t检验的P<0.05，说明两组数据间存在差异，但对子间均数差异变化不一致，均数差异可能还受其他因素的影响。
• 相关性检验P<0.05，但配对t检验的P>0.05，说明数据变化有一致性，但均数差异不显著，即研究因素未发挥作用。
• 相关性检验与配对t检验的P值均>0.05，说明数据在两组间不具备一致性，且差异也无统计学意义。