两变量间的关系包括确定性关系和非确定性关系两类。前者是指两变量间的关系是函数关系,即已知一个变量的值,可通过函数关系精确计算另一个变量的值。后者是指两变量宏观上存在关系,但并未精确到可以用函数关系来表示,这种既是必然的又是不确定的关系称为相关关系。相关关系分为线性和非线性相关,Pearson相关性分析是分析两变量间线性相关的方法。
关键词:相关分析; Pearson相关分析; 连续变量相关分析; Pearson相关系数
一、适用条件
Pearson相关性分析,需要满足5个条件:
条件1:两变量均为连续变量。
条件2:两变量应当是配对的,即来源于同一个个体。
条件3:两变量之间存在线性关系,通常绘制散点图检验。
条件4:两变量没有明显的异常值,通常绘制箱线图检验。异常值会对相关性分析的结果造成很大影响,如果存在异常值,应修改为正确值或进行变换去除,并在报告中指出。
条件5:两变量呈双变量正态分布或近似正态分布,通常绘制Q-Q图或进行正态性检验。
二、统计量计算
(一) Pearson相关系数
Pearson相关系数,又称积差相关系数,是表达两变量线性相关程度及方向的统计指标。样本的相关系数用符号r表示,总体相关系数用希腊字母ρ(英文rho,读作/ro/)表示。计算公式为:
\(r=\frac{\sum(X-\bar{X})(Y-\bar{Y})}{\sqrt{\sum(X-\bar{X})^{2} \sum(Y-\bar{Y})^{2}}}=\frac{l_{X Y}}{\sqrt{l_{X X} l_{Y Y}}}\)其中:
\(l_{X X}=(X-\bar{X})^{2}=\sum X^{2}-\frac{\left(\sum X\right)^{2}}{n}\),表示X的离均差平方和;
\(l_{Y Y}=(Y-\bar{Y})^{2}=\sum Y^{2}-\frac{\left(\sum Y\right)^{2}}{n}\),表示Y的离均差平方和;
\(l_{X Y}=\sum(X-\bar{X})(Y-\bar{Y})=\sum X Y-\frac{\left(\sum X\right)\left(\sum Y\right)}{n}\),表示X与Y的离均差平方和。
相关系数是一个无量纲的统计指标,其取值范围为-1≤r≤1,相关系数小于0为负相关,大于0为正相关,等于0表示不存在相关。相关系数的绝对值越大,表示两变量间的相关程度越密切。要确定是否存在线性关系,研究者需要查看两个变量的散点图,如果散点图大致呈一条直线,说明有线性关系,如果不是一条直线则没有线性关系。常见散点图提示的相关类型如图1所示。

(二) 相关系数的假设检验
样本相关系数r是总体相关系数ρ的估计值,与其他统计量一样,相关系数也有抽样误差。即使从一个相关系数ρ=0的总体中随机抽样,样本相关系数也往往不等于0。因此,在算得样本相关系数后,不能仅根据r的大小对两变量间是否有关系作出判断,需进一步检验r是否来自ρ=0的总体。相关系数的假设检验用t检验。
\(t=\frac{|r|}{S_{r}}=\frac{|r|}{\sqrt{\frac{1-r^{2}}{n-2}}}\)式中,\(\sqrt{\frac{1-r^{2}}{n-2}}\)为相关系数的标准误,记为Sr。
计算得到t值后,结合自由度ν=n-2,,查(t界值表),获得P值。
(三) 总体相关系数的区间估计
从相关系数ρ=0的总体中抽样,样本相关系数的抽样分布是对称的,当样本含量较大时,服从近似正态分布。但从相关系数ρ≠0的总体中抽样,样本相关系数的抽样分布是偏态的。上式表示的相关系数的分布服从自由度为n-2的t分布,仅在总体相关系数为0时成立。因此,不能用于相关系数的置信区间估计。R.A.Fisher(1921)提出的Z变换法解决了这个问题。对相关系数r作如下双曲正切变换(transformation of hyperbolic tangent):
\(Z=\tanh ^{-1} r=\frac{1}{2} \ln \left(\frac{1+r}{1-r}\right)\)其反双曲正切变换(transformation of inverse hyperbolic tangent)为:
\(r=\tanh z=\frac{e^{2 z}-1}{e^{2 z}+1}\)Fisher指出,所得变换值Z服从均数为\(\frac{1}{2} \ln \left(\frac{1+r}{1-r}\right)\),标准差为 \( \frac{1}{\sqrt{n-3}}\)的正态分布。因此,可先使用双曲正切变换式将r变换为Z,并按正态分布原理估计Z的置信区间:
\(Z\pm u_{\alpha} s_{\alpha}=Z \pm u_{\alpha} \frac{1}{\sqrt{n-3}}\)最后,使用反双曲正切变换式将所得Z的置信区间变换为总体相关系数ρ的置信区间。
三、案例数据
某研究者研究健康成年人的体重和双肾脏总体积(ml)的关系,测得24名健康成年人的体重wt (kg)与双肾脏总体积volume (ml),拟探讨健康成年人的体重与双肾体积是否有关。数据如图2所示。
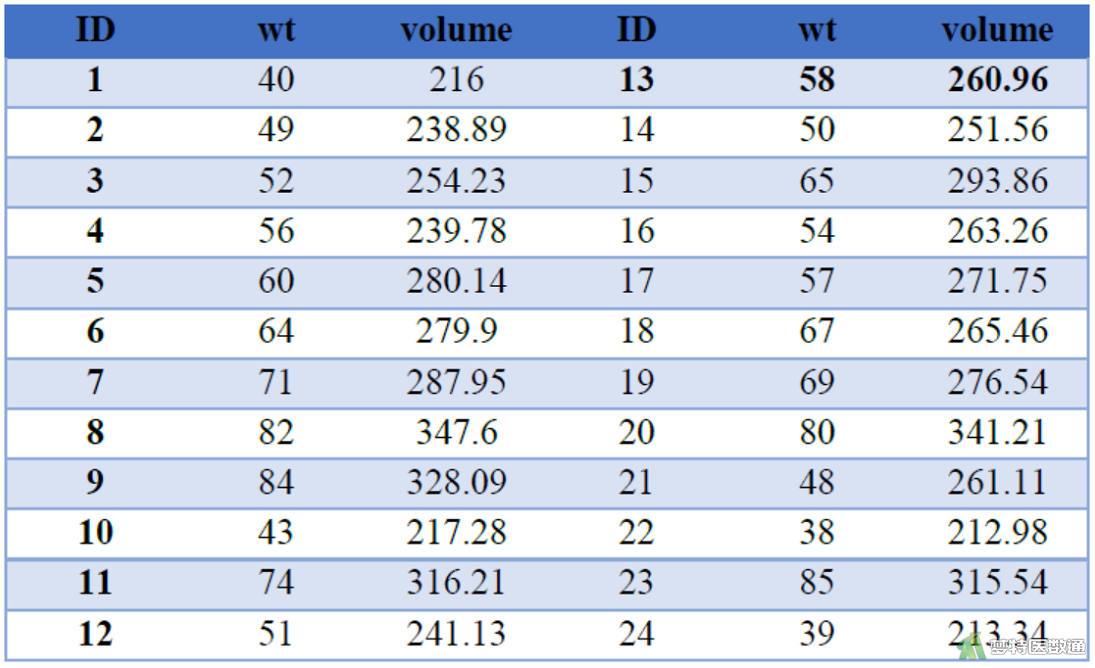
四、案例分析
(一) 适用条件判定
本案例探索体重和双肾体积的相关性,两变量均为连续变量,满足适用条件第一条;两变量均为同一位健康成年人的数据,满足适用条件第二条。
1. 线性关系检测
对体重和双肾体积绘制散点图,如图3所示,可见体重和双肾体积呈线性相关,满足适用条件第三条。
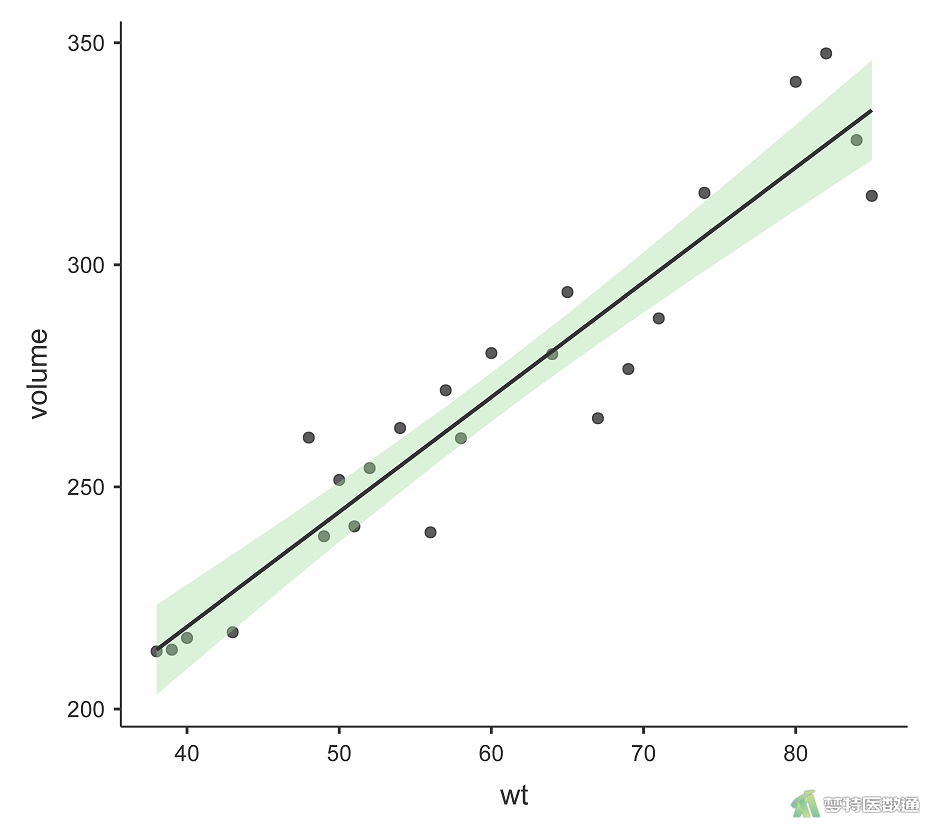
2. 异常值检测
对体重和双肾体积绘制箱线图,如图4-1、图4-2所示,体重和双肾体积均无明显异常值,满足适用条件第四条。
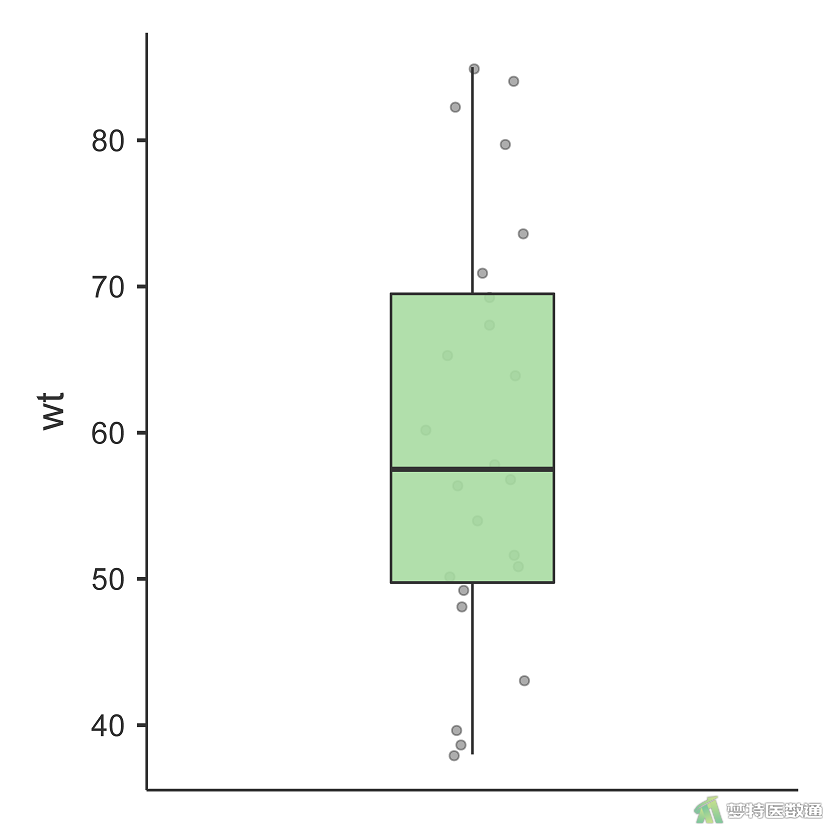
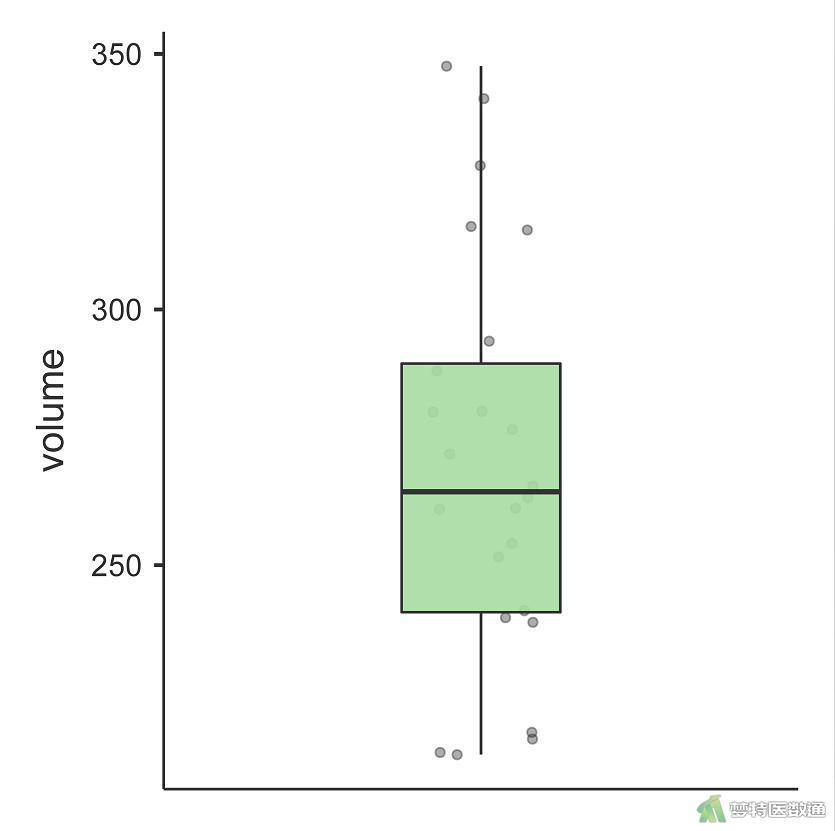
3. 正态性检测
Pearson相关分析要求变量呈双变量正态分布,而并非简单的要求两个自变量各自服从正态分布。有实验模拟显示,采用Shapiro-Wilk检验同时考察双变量正态分布和两变量分别的正态分布,在重复1万次服从两变量正态分布的实验中若以P=0.1为界值时,约有11%的实验不服从双变量正态分布;若以P=0.05为界值时,约有6%的实验不服从双变量正态分布。由于该条件比较宽松,因此可以考察两个自变量各自的正态分布情况代替分析双变量正态分布。
对体重和双肾体积绘制Q-Q图,如图5-1和5-2所示:
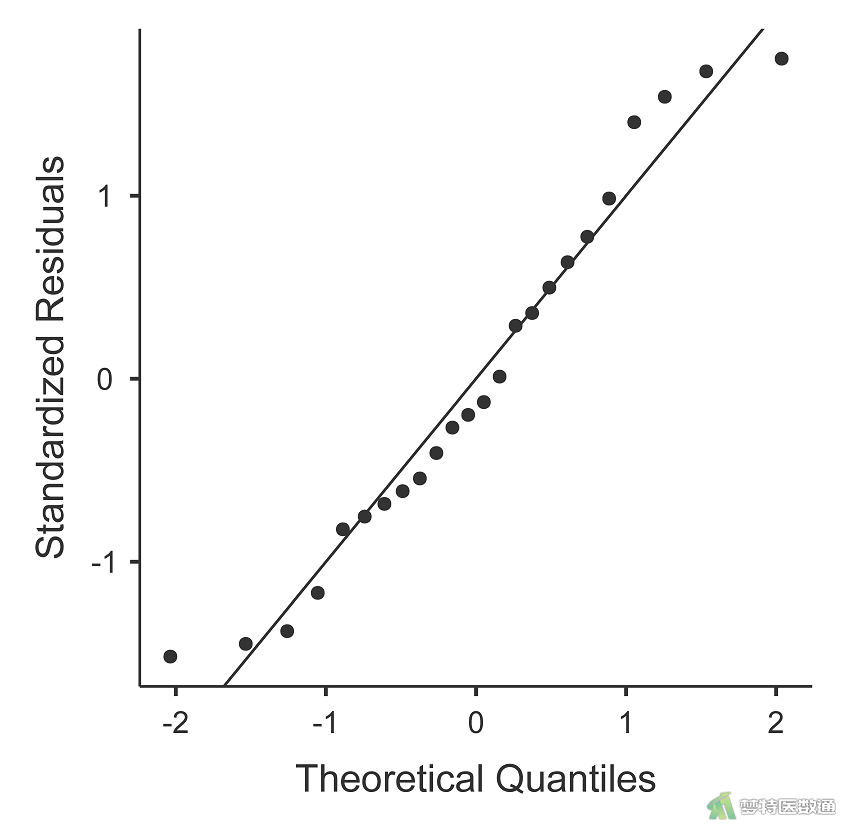
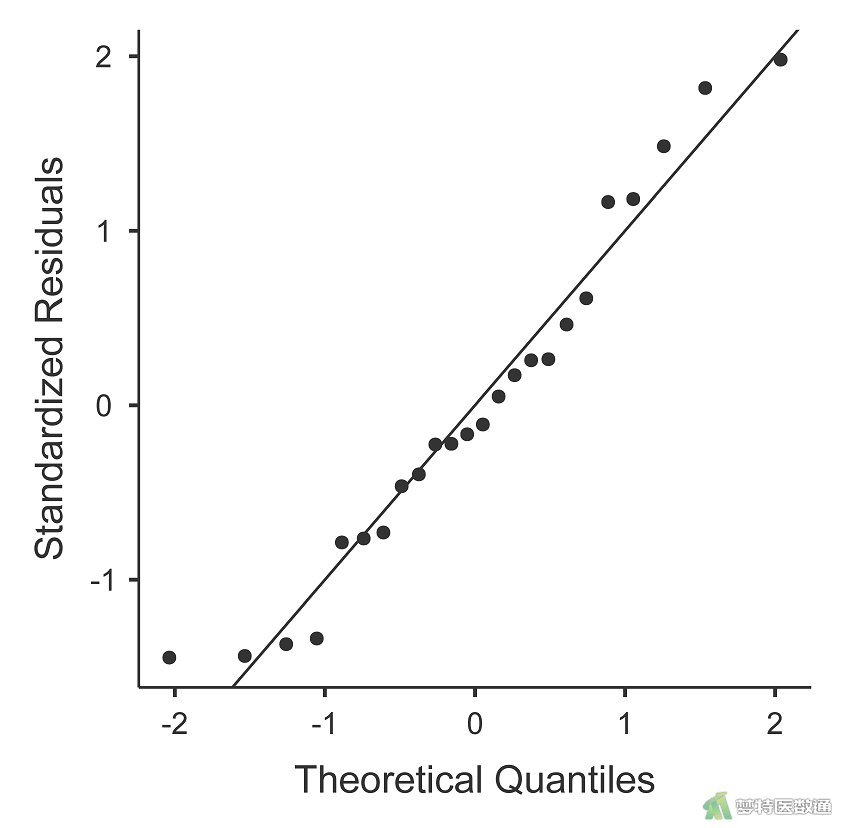
由Q-Q图可知体重和双肾体积均呈正态分布,满足适用条件第五条。
综上,本案例数据满足Pearson相关性分析的5个适用条件,可以使用Pearson相关性分析进行检验。
(二) 计算样本相关系数
根据本案例数据,可以计算得到:lXX=4761.33,lYY=35500.47,lXY=12307.53,根据相关系数r的计算公式,可以求得r=\(\frac{l_{X Y}}{\sqrt{l_{X X} l_{Y Y}}}=\frac{12307.53}{\sqrt{4761.33 * 35500.47}}=0.947\)
进一步检验r是否来自ρ=0的总体,步骤如下:
1. 建立检验假设,确定检验水准
H0:ρ=0,体重与双肾体积无相关关系
H1:ρ≠0,体重与双肾体积有相关关系
α = 0.05
2. 计算检验统计量t
\(t=\frac{|r|}{\sqrt{\frac{1-r^{2}}{n-2}}}=\frac{0.947}{\sqrt{\frac{1-0.947^{2}}{24-2}}}=13.778\)ν=n-2=24-2=22
3. 确定P值,作出推断结论
按自由度ν=22查(t界值表),得P<0.001。按α = 0.05水准,拒绝H0,接受H1,差异有统计学意义。即健康成年人的体重与双肾体积有正相关关系,相关系数r为0.947。
(三) 计算总体相关系数ρ的95%及99%置信区间
根据置信区间计算公式,可以计算得到:
\(z=\frac{1}{2} \ln \left(\frac{1+r}{1-r}\right)=\frac{1}{2} \ln \left(\frac{1+0.947}{1-0.947}\right)=1.798\) \(s_{z}=\frac{1}{\sqrt{n-3}}=\frac{1}{\sqrt{24-3}}=0.218\)可以计算得到Z的95%置信区间为:1.798±1.96×0.218=(1.371,2.226);Z的99%置信区间为:1.798±2.58×0.218=(1.235,2.361)。
由 \(r=\tanh z=\frac{e^{2 z}-1}{e^{2 z}+1}\)可计算总体相关系数ρ的95%置信区间的置信下限为:
\(r=\frac{e^{2 \times 1.371}-1}{e^{2 \times 1.371}+1}=0.879\)置信上限为:
\(r=\frac{e^{2 \times 2.226}-1}{e^{2 \times 2.226}+1}=0.977\)总体相关系数ρ的99%置信区间的置信下限为:
\(r=\frac{e^{2 \times 1.235}-1}{e^{2 \times 1.235}+1}=0.844\)置信上限为:
\(r=\frac{e^{2 \times 2.361}-1}{e^{2 \times 2.361}+1}=0.982\)即总体相关系数ρ的95%置信区间为0.879~0.977;ρ的99%置信区间为0.844~0.982。