独立样本Wilcoxon秩和检验(Wilcoxon Rank Sum Test)——SAS软件实现

关键词：SAS; 非参数检验; 秩和检验; Wilcoxon秩和检验; 独立样本秩和检验; Mann-Whitney U检验

一、案例介绍

某医师对12例高血压患者和11例糖尿病患者血清总胆固醇(TCHO)含量(mmol/L)进行了测定，问高血压患者和糖尿病患者的血清总胆固醇含量是否不同？创建代表组别的数值型变量“group(组别)”，赋值为“1”或“2”分别代表高血压患者和糖尿病患者。部分数据见图1。本文案例可从“附件下载”处下载。

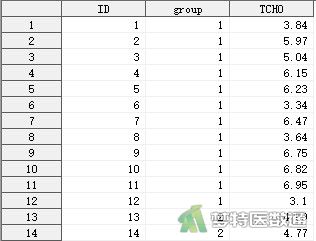
二、问题分析

本案例的分析目的是比较两组计量资料是否有差异，即判断高血压患者和糖尿病患者的血清总胆固醇含量是否不同。比较两组计量资料是否有差异可以使用两独立样本t检验或Wilcoxon rank-sum检验。如果数据满足正态性和方差齐性要求则可以使用两独立样本t检验。若满足正态性，不满足方差齐性，可使用校正t检验(Welch’s t检验)。但如果数据的方差相差太大，最好使用非参数检验(Wilcoxon rank-sum检验)。如果数据正态性和方差齐性都不满足，最好使用非参数检验(Wilcoxon rank-sum检验)。Wilcoxon rank-sum检验，需要满足三个条件：

条件1：有一个观察变量，且观察变量为连续变量(不满足正态分布或方差严重不齐)或等级变量。该条件需要通过软件判断或专业判断。

条件2：有一个分组变量，且为二分类。本研究中分为高血压患组和糖尿病组，该条件满足。

条件3：具有相互独立的观测值。本研究中各研究对象的TCHO含量都是独立的，不存在互相干扰的情况，该条件满足。

三、软件操作及结果解读

(一) 导入数据

①利用LIBNAME语句建立SAS逻辑库关联，注意逻辑库名称要求，即最大长度8字符，必须以字母或下划线“_”开始，可以是字母、数字和下划线的任意组合。具体代码如下：

libname mydata "D:\mydata";

通过这一步骤，SAS能够识别引号中的物理位置，将逻辑库建立在该目录下，同时在以下过程中新建的SAS表格便可以永久储存在该位置，便于反复读取和使用。先运行该代码使其生效。

②利用PROC IMPORT语句导入文件，代码如下：

proc import out= mydata.example
datafile=" D:\mydata\Wilcoxon秩和检验.csv"
dbms=csv replace;
getnames=yes;
run;

该过程在mydata逻辑库中生成example数据集，数据文件由DATAFILE=选项指定，DBMS=选项指定其数据库类型。该案例中初始数据集为csv文件，故而使用“dbms=csv”指定。如果已经存在相同名称的SAS数据集，即可使用REPLACE选项进行覆盖。GERNAMES=YES选项指定从第2行开始读取数据，将数据集的首行变量名作为SAS数据集的变量名。

(二) 适用条件判断

1. 条件1判断(正态性检验)

(1) 软件操作

运用UNIVARIATE 过程进行正态性检验，示例代码如下：

proc univariate data= mydata.example plot normal;
class group;
var TCHO;
Histogram /normal kernel;
run;

其中“mydata.example”为上一步中导入的数据集名称，“TCHO”为分析变量名，即血清总胆固醇含量。选项PLOT产生了平行条状图，箱线图和正态概率图，高血压患者(group=1)和糖尿病患者(group=2)的结果分别如图2和图3所示。

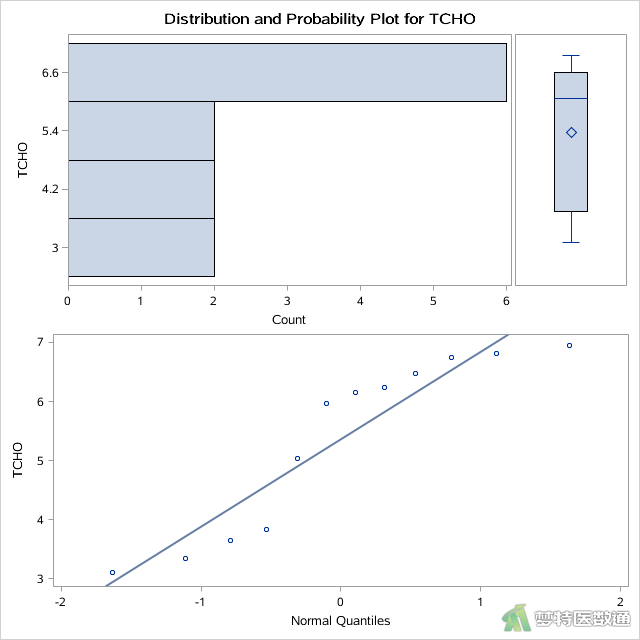
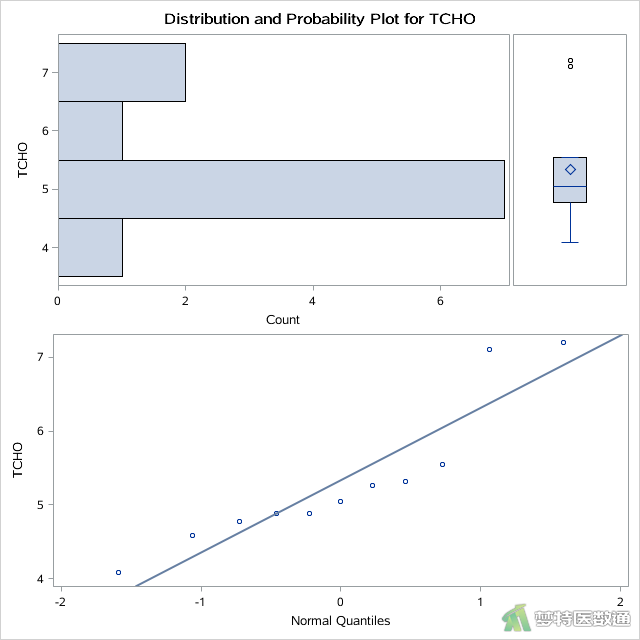
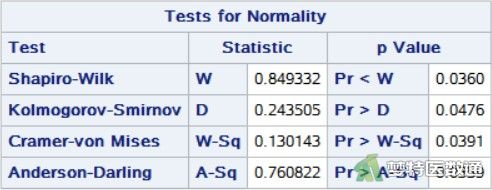
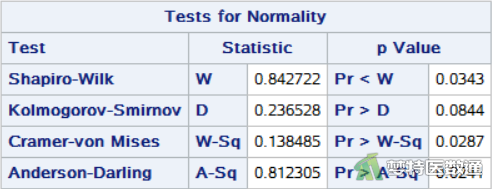
选项NORMAL进行正态性检验，得到“Tests for Normality (正态性检验)”结果，高血压患者(group=1)和糖尿病患者(group=2)的结果如图4和图5所示。

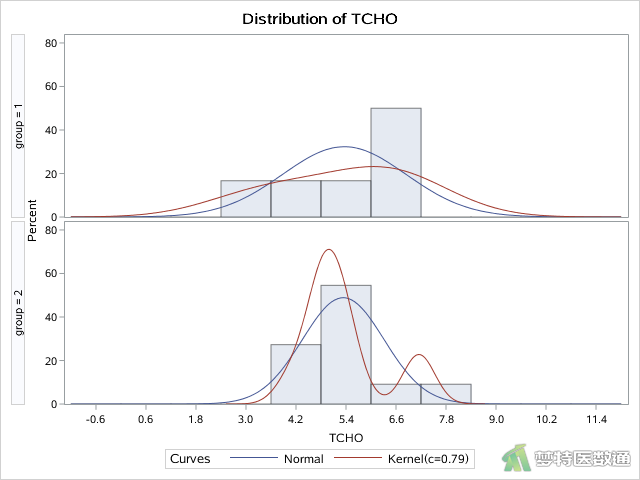
HISTOGRAM语句可以针对指定变量“TCHO”绘制直方图，该语句中NORMAL选项可作正态分布的密度曲线，而KERNERL选项可作基于数据的核分布密度曲线，可直观展示变量的分布情况，如图6所示。

(2) 结果解读

正态性检验结果如图4和图5所示，分别给出了四种种正态性检验的结果，其中较为常用的为Shapiro-Wilk (夏皮罗-威尔克正态性，S-W)检验和Kolmogorov-Smirnov (柯尔莫哥洛夫-斯米诺夫，K-S)检验。K-S检验适用于大样本资料，本案查看S-W检验结果。高血压患者(group=1)和糖尿病患者(group=2)的血清总胆固醇含量结果分别为P=0.0360和0.0343，均<0.1，提示数据不服从正态分布；图2和图3中，高血压患者(group=1)和糖尿病患者(group=2)的Q-Q图上散点与对角线的分布重合度较低，且图6中数据的核分布密度曲线与正态分布密度曲线重合度较低，也可以认为数据为非正态分布。关于正态性检验的注意事项详见文章(医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现)(链接)。

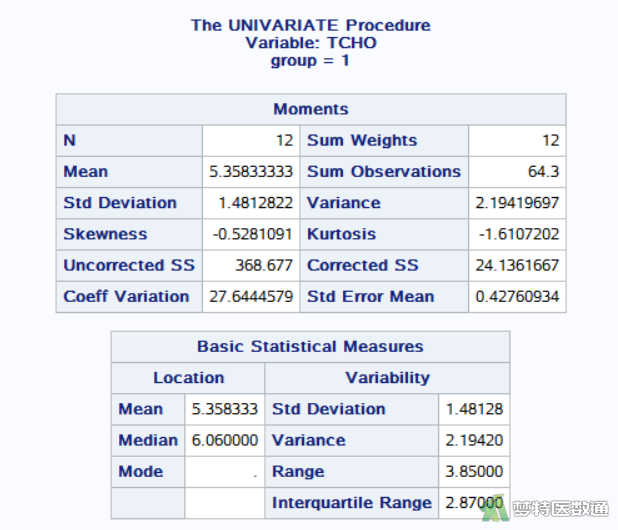
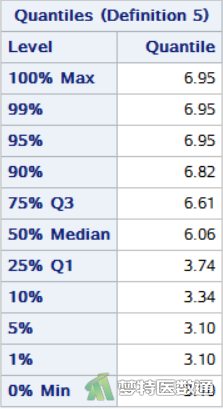
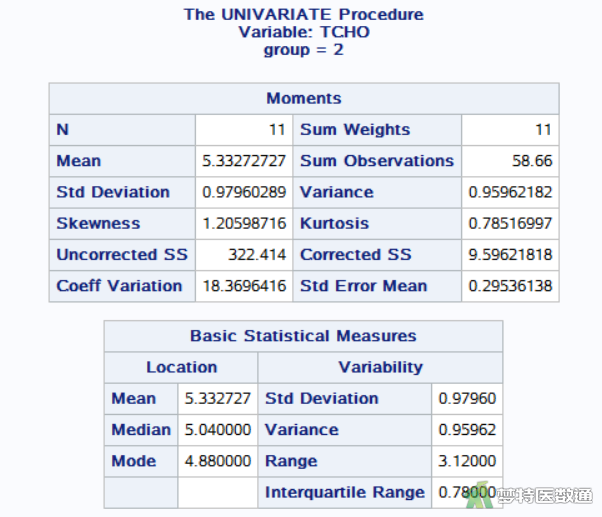
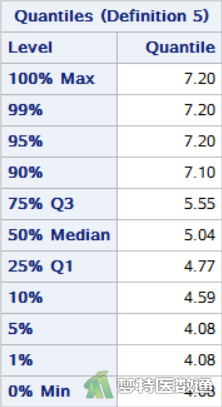
图7和图8是对高血压患者(group=1)的“Basic Statistical Measures (基本统计描述)”结果，包括变量“TCHO”的“N (样本量)”、“Mean(均值)”、“Median(中位数)”、“Std. Deviation(标准差)”、 “Min(最小值)”、“Max(最大值)”、“25% Q1(第1四分位数)”、50% Median(中位数)和“75% Q3(第3四分位数)”等指标。图9和图10显示了糖尿病患者(group=2)的血清总胆固醇含量的“Basic Statistical Measures (基本统计描述)”结果。可知高血压组(group=1)和糖尿病组(group=2)患者的TCHO中位数(四分位间距)分别为6.06 (2.87) mmol/L和5.04 (0.78) mmol/L。

注意：计算四分位数间距时，通常将n个变量值从小到大排列。SAS中默认采用基于经验分布函数的平均，百分位次为n×P%=j+g，其中P指的是P百分位数，j为整数部分，g为小数部分，即当g=0时，该P百分位数P_x=(X_j+X_j+1)/2，当g>0时，P_x=X_j+1 (X_j为此数列中的第j个数)。

SPSS中存在计算结果不一致的情况，其原因是SPSS默认的计算方式为，以(n+1)×P%=j+g为百分位次，当g=0时，P_x= X_j，当g>0时，P_x= g×X_j+1+(1-g) X_j。

2. 条件2判断(方差齐性检验)

(1) 软件操作

①通过ANOVA过程得到方差齐性检验结果(图11)：

proc anova data = mydata.example;
	class group;
 model TCHO = group;
	means group / hovtest=levene(type=abs);
run;

该步骤中，CLASS语句指定分类变量，即“group”变量。MODEL语句指定分析因素与响应变量，即按照“group”分组对“TCHO”变量分析。MEANS语句计算均数和方差，其常见选项HOVTEST可指定分析方法，此处我们使用LEVENE检验，“(type=abs)”指定该过程计算绝对值(absolute value)进行分析。

(2) 结果解读

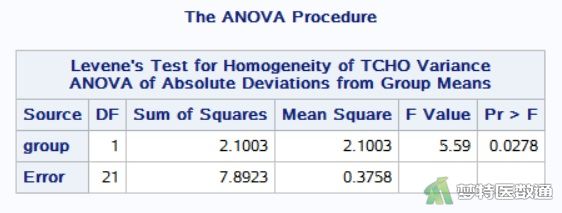
图11是“The ANOVA Procedure (方差齐性检验)”结果，可知“Levene Statistic(Levene统计量)” F=5.59，P=0.0278<0.1，提示两组数据方差不齐。关于方差齐性检验的更多内容请阅读(医学统计学核心概念及重要假设检验的软件实现(4/4)——方差齐性检验及SPSS实现)。

综上，本案例中两组连续变量数据既不服从正态分布，也不满足方差齐性，可以考虑使用Wilcoxon rank-sum 检验。

(三) 统计描述及推断

1. 软件操作

通过NPAR1WAY过程得到检验结果，如图12所示：

proc npar1way data=mydata.example wilcoxon;
class group;
var TCHO;
exact;
run;

其中，EXACT语句可计算精确P值。

注意：此处“NPAR1WAY”中为数字“1”，而非英文字母“I”或“L”。

2. 结果解读

(1) 统计描述

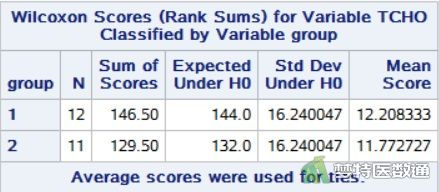
Wilcoxon rank-sum检验是将原始数据排序后分配秩次进行的假设检验，所以图13 由NPAR1WAY过程得到的“Wilcoxon Scores (Rank Sums) for Variable TCHO Classified by Variable group (以“group”分组的变量“TCHO”的Wilcoxon秩次(秩和))”的结果表，是对两组变量秩次的统计描述。可见高血压组(group=1)和糖尿病组(group=2) “N(样本量)”分别为12和11，“Mean Score(平均秩次)”分别为12.21和11.77。从上述正态性检验结果中可知，高血压组和糖尿病组的中位数(四分位间距)分别为6.06 (2.87) mmol/L和5.04 (0.78) mmol/L。两组数值较为接近，提示TCHO含量可能不存在差异，但还需要依据统计学检验的结果进行判断。

(2) 统计学推断

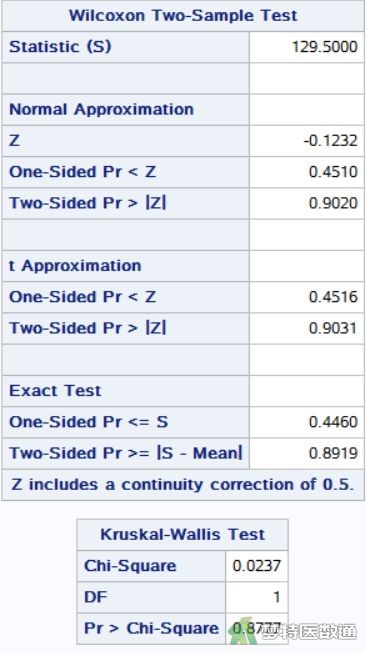
图12是“Wilcoxon Two-sample Test (Wilcoxon 两样本检验)”的结果，其中“Statistic”表示统计量S=129.500，“Standardized Test Statistic (标准化检验)”统计量为Z=-0.1232， P值为0.9020。“Exact Test (精确检验)”结果精确P值为0.8919。样本量越大，渐进P值就会越接近真实P值。如果每组样本量均小于20，以精确P值进行假设检验的判断。如果每组样本量均大于20，渐进P值可以较好的代表真正的P值，此时可以选择渐进P值进行假设检验的判断。本案例中两组样本量均小于20，查看精确P值=0.8919>0.05，所以尚不能认为高血压患者和糖尿病患者的TCHO含量不同。

注意：SAS结果中统计量S=129.500，而SPSS得到结果为U=63.500，其转换公式为U=S－n(n+1)/2，其中n为样本量较小组的例数。

四、结论

本研究采用Wilcoxon rank-sum 检验判断高血压患者和糖尿病患者的TCHO含量是否不同。通过Q-Q图和Shapiro-Wilk检验，提示两组数据不服从正态分布；通过Levene’s检验，提示两组数据总体方差不齐，符合使用Wilcoxon rank-sum 检验的条件。

结果显示，高血压患者和糖尿病患者TCHO中位数分别为6.06 (2.87) mmol/L和5.04 (0.78) mmol/L，平均秩次分别为12.21和11.77。Wilcoxon rank-sum 检验结果显示，两组人群TCHO含量差异无统计学意义(S=129.500，P=0.8919)。因此，尚不能认为高血压患者和糖尿病患者的血清总胆固醇含量不同。