独立样本Wilcoxon秩和检验(Wilcoxon rank sum test)用于推断计量资料或等级资料的两个独立样本所来自的两个总体分布位置是否有差别。
关键词:非参数检验; 秩和检验; Wilcoxon秩和检验; 独立样本秩和检验; Mann-Whitney U检验
无论两个总体分布的形状有无差别,秩和检验的目的是推断两个总体分布的位置是否有差别,这正是实践中所需要的,如要推断两个不同人群的某项指标值的大小是否有差别或哪个人群的大,可用其指标值分布的位置差别反映,而不关心其指标值分布的形状有无差别。
两样本比较的秩和检验的基本思想是:如果待比较的两样本(样本含量分别为n1及n2)来自位置相同的两个总体(即H0成立),则含量为n1的样本之实际秩和T与其理论秩和n1 (N+1)/2之差[T- n1 (N+1)/2]纯系抽样误差所致,故此差值一般不会很大,而差值越大的概率越小。若从现有样本中算得的T与其理论秩和相差很大,则说明从H0规定的总体中随机抽得现有样本及更极端样本的概率P很小,如小于等于检验水准a,则可拒绝H0。本篇文章将举例介绍Wilcoxon秩和检验的假设检验理论。
一、适用条件
1. 有一个观察变量,且观察变量为连续变量(不满足正态分布或方差不齐或分布未知)或等级变量。
2. 有一个分组变量,且为二分类。
3. 观测值相互独立。
二、统计量计算
(一) T值法
T值法是指对数据编秩计算后,通过T值表确定P值,做出统计推断。
1. 检验统计量T值的计算
(1)计量资料检验统计量T值的计算
①把两样本数据混合从小到大编秩,遇数据相等者取平均秩;②以样本例数小者为n1,其秩和T1为T,若两样本例数相等,可任取一样本的秩和(T1或T2)为T。
(2)频数表资料和等级资料检验统计量T值的计算
①频数表资料是按数量区间分组,等级资料是按等级分组。需要先确定各等级的合计人数、秩次范围和平均秩次;②通过样本例数×平均秩次求各等级的秩和;③以样本例数小者为n1,其秩和(T1)为T,若两样本例数相等,可任取一样本的秩和(T1或T2)为T。
2. 确定P值,做出统计推断
当n1≤10和n2-n1≤10时,查(T界值表)。查表时,先找到n1与n2-n1相交处所对应的4行界值,再逐行将检验统计量T与界值相比,若T值在界值范围内,其P值大于相应概率水平;若T值恰好等于界值,其P值等于(一般是近似等于)相应概率水平;若T值在界值范围外,其P值小于相应概率水平。
3. T界值表制作的原理
为简单起见,假定两个样本例数n1=2,n2=5,则N= n1+n2=7,总体秩为1,2,3,4,5,6,7。样本例数n1=2从总体中取2个秩,取秩的21种\(\left[\left(\begin{array}{l}7 \\2\end{array}\right)=21\right]\)可能组合情况及秩和T值如图1。
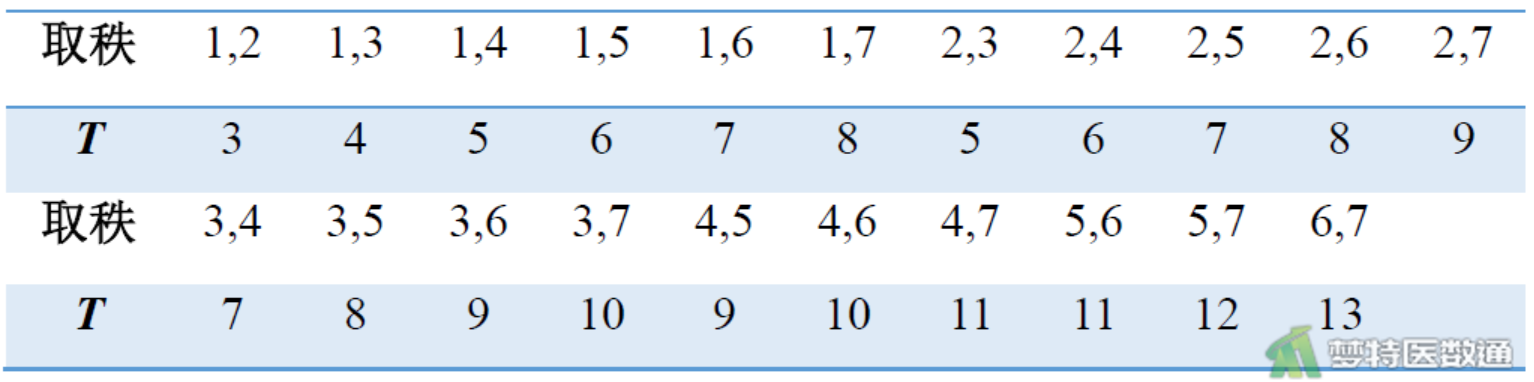
每种组合情况所对应T取值的概率为1/21=0.0476,归纳成N =7和n1=2时T的概率分布见图2。

T的概率分布是对称的非连续分布。T的最小值为n1(n1+1)/2(1+2+…+n1),最大值为n1n2+n1(n1+1)/2[(n2+1)+(n2+2)+…+(n2+n1)],均数为n1(N+1)/2。如N=7和n1=2时(n2=5),T的最小值为3,最大值为13,均数为8。两个样本的秩和之和T1+T2= N (N+1)/2。
根据图2可计算N=7和n1=2时T的单侧和双侧累计概率。如T为3~13的单侧累计概率为0.0476(近似0.05),双侧累计概率等于0.0952(近似0.10),这就是(T界值表)中的n1=2和n2-n1=3时T界值的来源。无论N和n1如何取值,其T界值的制作步骤与N=7和n1=2时相同。
(二) 正态近似法
当n1>10或n2-n1>10,T分布接近均数为n1(N+1)/2,方差为n1n2(N+1)/12的正态分布,故可按下式直接计算u值,按标准正态分布界定P值并做推断结论。
\( u=\frac{|T-n_1(N+1)/2|-0.5}{\sqrt{n_1n_2(N+1)/12}} \)公式中的0.5是连续校正系数,因为u分布是连续的,而T分布是不连续的。
在无相同观察值(即无相同秩次“ties”)或相同秩次不太多时近似程度较好,但若相同秩次较多时(如超过25%),用上式计算的u值偏小,可按下式进行校正。u值经校正后略增大,P值相应减少。
\( u_c=u/\sqrt{C} \)式中 \(C=1-\sum(t_j^3-t_j)/(N^3-N) \) ,tj为第j个相同秩次的个数。
(三) Mann-Whitney U检验
两独立样本比较还常用Mann-Whitney U检验(Mann-Whitney U test)。检验统计量U为:把第一个样本的n1 (n1≤n2)个变量值的每个变量值,与第二个样本的n2个变量值逐个比较,小于记1,相等记0.5,大于记0,求其和。当n1和n2均较小时,如n1+n2≤30,使用专门的(U界值表)进行统计学推断;当n1和n2均较大时,用正态近似法作u检验。
U的概率分布是对称的非连续分布。Mann-Whitney U检验的U和Wilcoxon秩和检验的T有一定的关系。当第一个样本的每个变量值都小于第二个样本的所有变量值时,U= n1n2,T= n1(n1+1)/2;当第一个样本的每个变量值都大于第二个样本的所有变量值时,U=0,T=n1n2+n1(n1+1)/2。T每增加(或减少)1,U就减少(或增加)1,即有U=n1n2+n1(n1+1)/2-T。故得U的均数和方差:μU=n1n2+n1(n1+1)/2-n1(N+1)/2= n1n2/2, \( \sigma_{U}^{2}=\sigma_{T}^{2} \) 。因此有:
\( u=\frac{U-n_1n_2/2}{\sqrt{\frac{n_1n_2(N+1)}{12}\left(1-\frac{\sum(t_j^3-t_j)}{N^3-N}\right)}} \)三、案例数据
某医师对12例高血压患者和11例糖尿病患者血清总胆固醇(TCHO)含量(mmol/L)进行了测定,问高血压患者和糖尿病患者的血清总胆固醇含量是否不同?数据见图3。

四、假设检验
本例两样本资料经“Normality Test (Shapiro-Wilk) (夏皮罗-威尔克正态性)”正态性检验结果显示两组的P值为0.036和0.034,均<0.1,提示两组数据不服从正态分布。并且经Levene方差齐性检验显示:F=5.589,P=0.028<0.1提示两组数据方差不齐。本案例中两组连续变量数据既不服从正态分布,也不满足方差齐性条件,可使用两独立样本比较的Wilcoxon秩和检验。
(一) 建立检验假设,确定检验水准
H0:高血压患者和糖尿病患者血清总胆固醇(TCHO)含量总体分布位置相同
H1:高血压患者和糖尿病患者血清总胆固醇(TCHO)含量总体分布位置不同
α = 0.05
(二) 计算检验统计量
1. 编秩
(1) 将两组数据混合从小到大编秩次(即编秩序号),若遇到数据相等的,则取平均秩。
(2) 求秩和。以样本例数小者为n1,其秩和(T1)为T,若两样本例数相等,可任取一样本的秩和(T1和T2)为T。
2. 计算T值
据图3“秩”栏可得,取 n1=11,T=129.5。
(三) 确定P值,作出推断结论
案例数据中例数较少的一组样本量n1=11>10,可采用正态近似法,n1+n2=N利用公式求得:
\( u=\frac{\left|T-n_{1}(N+1) / 2\right|-0.5}{\sqrt{n_{1} n_{2}(N+1) / 12}}=\frac{|129.5-11(23+1) / 2|-0.5}{\sqrt{11 \times 12(23+1) / 12}}=0.12309 \)本例相同秩次为4个,未超过25%,近似程度较好,不需进行校正。若对其进行校正,则按以下公式进行计算:
\( \mathrm{C}=1-\sum\left(t_{j}^{3}-t_{j}\right) /\left(N^{3}-N\right)=1-\left[\frac{\left(2^{3}-2\right)+\left(2^{3}-2\right)}{23^{3}-23}\right]=0.9990119 \) \( u_{c}=u / \sqrt{C}=0.12309 / \sqrt{0.9990119}=0.1231509 \)可见校正前后数值相差不大。
查U界值表可知,0.1231509<u0.05,2=1.96,P>0.5
按α = 0.05水准,不拒绝H0,尚不能认为高血压患者和糖尿病患者的血清总胆固醇含量不同。