无序多分类Logistic回归分析(Multinomial Logistic Regression Analysis)——SAS软件实现

关键词：SAS; 无序多分类logistic回归; 无序logistic回归; 无序逻辑回归

一 、 案例介绍

欲探索性别与年龄是否对某中医证型的分类有影响，从医院数据库中随机选择了200例样本进行分析。部分数据见图1。本文案例可从“附件下载”处下载。其中，ID表示样本序号；gender表示性别(1=男, 2=女)；age表示年龄(1=<40岁、2=40-59岁、3=≥60岁)；TCM表示中医证型(1=A型、2=B型、3=C型)。

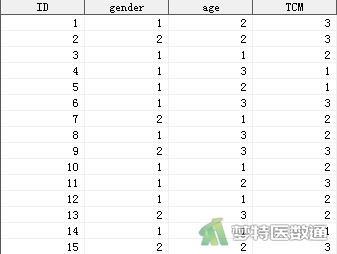
二、问题分析

本案例中，因变量“中医证型”为无序多分类变量，欲探索“性别”与“年龄”是否对“中医证型”分类有影响，可将“中医证型”的某一类别设置为对照组，通过无序多分类logistic回归分析将另外两种不同类别证型的样本分别与对照组进行对比，得到“性别”、“年龄”与这两种类别证型的暴露-风险关系。无序多分类logistic回归需要满足3个条件：

条件1：因变量唯一，且为无序多分类变量，本案例符合。

条件2：存在一个或多个自变量，可为定性与定量变量，本案例符合。

条件3：一般要求例数较少类的样本量为自变量个数的10~15倍(EPV原则)且经验上每组的人数最好多于30例，参照水平组不应少于30或50例。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件3判断(因变量样本例数)

(1) SAS实现

首先导入数据，代码如下：

proc import datafile="G: \test\无序多分类logistic回归.csv" dbms=csv out=data1;
run;

使用如下的proc freq过程步，统计因变量每类的样本例数。

proc freq data=data1;
	tables TCM;
run;

(2) 结果解读

如图2所示，因变量中医证型“A”(TCM=1)、“B” (TCM=2)、“C” (TCM=3)的例数分别为60、74和66，均>30例。根据“例数较少类的因变量例数为自变量个数的10~15倍(EPV原则)”，本案例可纳入4~6个自变量进行多因素无序多分类logistic回归分析。

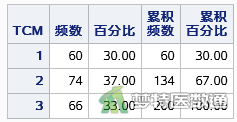
2. 条件3判断(自变量样本例数)

(1) SAS实现

使用如下的proc freq过程步，统计分类变量gender、age各类别的因变量例数。

proc freq data=data1;
	tables TCM *gender;
run;
proc freq data=data1;
	tables TCM *age;
run;

(2) 结果解读

年龄和性别与中医证型的交叉表如图3和图4所示，可见年龄水平为“<40”(age=1)和“≥60” (age=3)时因变量的例数<30(图3)，如果“年龄”在多因素分析过程中进入模型，应注意避免例数较少的水平被选为参照，若实在不能避免，在结果解释时应注意其局限性。

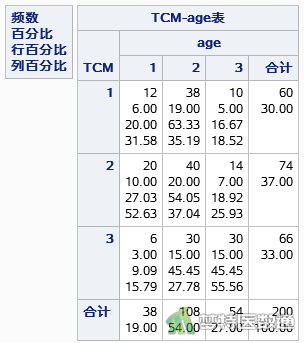
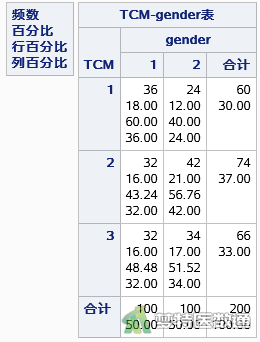
(二) 统计推断

1. SAS实现

proc logistic data=data1;	
	class gender(param=reference ref="2");
	class age(param=reference ref="3");
	model TCM(ref="3")=gender age/link=glogit stb rsquare;
quit;

其中,class选项对分类自变量设置参照，本例以女性(gender="2")和年龄≥60岁(age="3")为参照。Model语句中的TCM(ref="3")设置因变量以中医证型C型(TCM ="3")为参照；link=glogit表示拟合多分类无序logistic回归；stb选项输出标准回归系数；rsquare选项输出模型R²的值。

2. 结果解读

(1) 模型评价

如图5所示，模型（不带协变量）AIC 、SC和-2 Log L值分别为441.970、448.566、437.970，模型（带协变量）AIC 、SC和-2 Log L值分别为428.262、454.649、412.262。模型R²值为0.121，最大重新换算R²值为0.136，R²值越接近1表明模型拟合度越高，因此表明本数据集模型拟合度一般。似然比检验χ²=25.707，P=0.0003，表明模型有统计学意义。此外，图5的最后一个结果表格还列出了每个自变量在模型中是否有统计学意义。可知，性别“gender”在模型中无统计学意义(χ²=5.561，P=0.062)，应该被移除模型。年龄“age”在模型中有统计学意义(χ²=20.263，P<0.001)，应该保留在模型中。但考虑到本案例只有2个自变量，此次分析过程中仍然将两个自变量保留在多因素分析模型中。

(2) 拟合优度

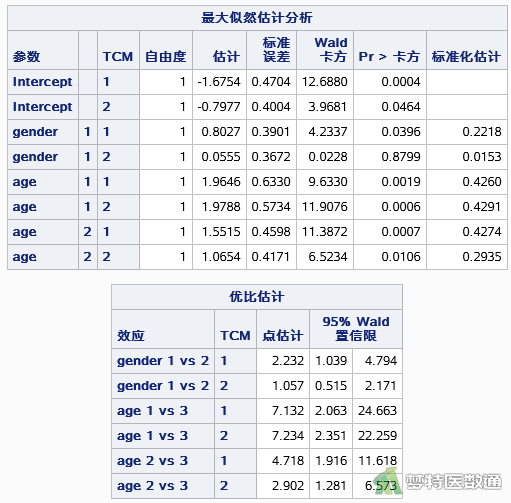
图6展示了中医证型A与C 相比、B与C相比时模型的参数估计。当中医证型A与C 相比时，性别的P=0.040，但这并不能表示性别在模型中具有统计学意义，因为该变量的整体检验并无统计学意义。年龄<40岁的患者出现A型的风险是年龄≥60岁的7.132倍 (95%CI：2.063~24.663；P=0.002)，年龄40-59岁的患者出现A型的风险是年龄≥60岁的4.718倍(95%CI：1.916~11.618；P=0.001)。拟合的模型为：

Logit(A/C)=-1.675+0.803*(gender=1)+1.965*(age=1)+1.552*(age=2)

当中医证型B与C 相比时，性别的P=0.880，无统计学意义。年龄<40岁的患者出现B型的风险是年龄≥60岁的7.234倍 (95%CI：2.351~22.259；P<0.001)，年龄40-59岁的患者出现B型的风险是年龄≥60岁的2.902倍(95%CI：1.281~6.573；P=0.011)。拟合的模型为：

Logit( B/C)=-0.798+0.056*(gender=1)+1.979*(age=1)+1.065*(age=2)

3. 补充分析

上述分析是以因变量C水平为参照得出的分析结果，可知A与C、B与C相比的情况，但是不知道B与A相比的情况。此处以水平A为参照进行分析。

(1) SAS实现

proc logistic data=data1;	
	class gender(param=reference ref="2");
	class age(param=reference ref="3");
	model TCM(ref="1")=gender age/link=glogit stb rsquare;
quit;

(2) 结果解读

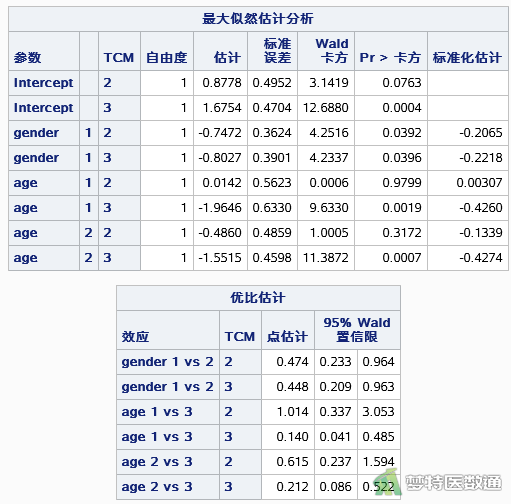
图7展示了中医证型B与A相比、C与A相比时模型的参数估计。当中医证型B与A相比时，性别的P=0.039，但这并不能表示性别在模型中具有统计学意义，因为该变量的整体检验并无统计学意义。年龄<40岁的患者和年龄40-59岁的患者出现B型的风险与年龄≥60岁的患者相比，也均无统计学差异(P=0.980和P=0.317)。C与A比较的结果等价于图6中A与C比较的结果。

四、结论

本研究采用无序多分类Logistic回归探讨性别和年龄是否对某中医证型的分类有影响。因变量例数分布满足样本量需求。

模型（不带协变量）AIC 、SC和-2 Log L值分别为441.970、448.566、437.970，模型（带协变量）AIC 、SC和-2 Log L值分别为428.262、454.649、412.262。模型R²值为0.121，最大重新换算R²值为0.136，R²值越接近1表明模型拟合度越高，因此表明本数据集模型拟合度一般。似然比检验χ²=25.707，P=0.0003，表明模型有统计学意义。性别“gender”在模型中无统计学意义(χ²=5.561，P=0.062)，年龄“age”在模型中有统计学意义(χ²=20.263，P<0.001)。

当中医证型A与C 相比时，性别的P=0.040，但这并不能表示性别在模型中具有统计学意义，因为该变量的整体检验并无统计学意义。年龄<40岁的患者出现A型的风险是年龄≥60岁的7.132倍 (95%CI：2.063~24.663；P=0.002)，年龄40-59岁的患者出现A型的风险是年龄≥60岁的4.718倍(95%CI：1.916~11.618；P=0.001)。

当中医证型B与C 相比时，性别的P=0.880，无统计学意义。年龄<40岁的患者出现B型的风险是年龄≥60岁的7.234倍 (95%CI：2.351~22.259；P<0.001)，年龄40-59岁的患者出现B型的风险是年龄≥60岁的2.902倍(95%CI：1.281~6.573；P=0.011)。

当中医证型B与A相比时，性别的P=0.039，但这并不能表示性别在模型中具有统计学意义，因为该变量的整体检验并无统计学意义。年龄<40岁的患者和年龄40-59岁的患者出现B型的风险与年龄≥60岁的患者相比，也均无统计学差异(P=0.980和P=0.317)。

五、知识小贴士

• 无序多分类logistic回归的因变量为多分类变量，内部分析过程是选择一个参照组将因变量拆分为多个二分类变量，拟合多个二项logistic回归。
• 由于无序多分类logistic回归的本质是多个二项logistic回归，因此其结果解读可参考二项logistic回归，只是每个变量需要在多个二项logistic回归中分别解读。
• 在“中医证型”B与C的比较以及B与A的比较中，可发现自变量“性别”有统计学意义，但由于整体检验该变量并无统计学意义，因此尚不能认为“性别”对中医证型的分类有影响。