无序多分类logistic回归分析(Multinomial Logistic Regression Analysis)——理论介绍

关键词：无序多分类logistic回归; 无序logistic回归; 无序逻辑回归

一、基本概念

对于无序多分类logistic回归，可将其看作非条件二分类logistic回归的扩展。分析过程是将多分类因变量拆分成多个二分类变量，拟合n-1个(n为因变量的分类数)二分类logistic回归，变量的回归系数β、效应量OR值的计算等在n-1个模型中分别进行。假设某一疾病有A、B、C三个中医证型，将其分别赋值为1、2、3，若以A证型为参照，那么该模型的表示如下：

\(\begin{aligned}\operatorname{logit}[P(Y=&2 \mid X)]=\ln \left[\frac{P(Y=2 \mid X)}{P(Y=1 \mid X)}\right] \\=& \beta_{20}+\beta_{21} X_{1}+\beta_{22} X_{2}+\cdots+\beta_{2 m} X_{m}\end{aligned}\)

\(\begin{aligned}\operatorname{logit}[P(Y=&3 \mid X)]=\ln \left[\frac{P(Y=3 \mid X)}{P(Y=1 \mid X)}\right] \\=& \beta_{30}+\beta_{31} X_{1}+\beta_{32} X_{2}+\cdots+\beta_{3 m} X_{m}\end{aligned}\)

二、适用条件

无序多分类logistic回归需要满足3个条件：

条件1：因变量唯一，且为无序多分类变量。

条件2：存在一个或多个自变量，可为定性与定量变量。

条件3：一般要求例数较少因变量类的观察例数为自变量个数的10~15倍(EPV原则)且经验上每组的人数最好多于30例，自变量的参照水平组不应少于30或50例。

三、参数估计

变量回归系数的估计与二分类logistic回归类似，详见(二分类logistic回归分析(Binomial Logistic Regression Analysis)——理论介绍)。

四、假设检验

模型和变量回归系数的假设检验与二分类logistic回归的类似，详见(二分类logistic回归分析(Binomial Logistic Regression Analysis)——理论介绍)。

五、案例分析

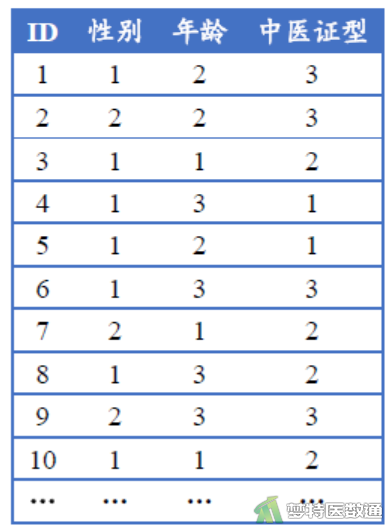
欲探索性别(1=“男性”、2=“女性”)与年龄(岁，1=“<40”、2=“40-59”、3=“≥60”)是否对某中医证型(1=“A”、2=“B”、3=“C”)的分类有影响，从医院数据库中随机选择了200例样本进行分析。部分数据如图1所示。

本案例以中医证型“C”作为参照，拟合无序多分类logistic回归。通过软件分析可得到每个自变量对应的Wald χ²值、截距、每个自变量的哑变量对应的回归系数和Wald χ²值。

(一) 回归模型检验

对该模型进行整体假设检验，步骤如下：

1. 建立假设检验，确定检验水准

H₀：β₂₁=β₂₂ =β₃₁=β₃₂= 0

H₁：β_ij (i=2、3，j=1、2)不全为0

α=0.05

2. 计算检验统计量

通过软件可计算得到无序多分类logistic回归模型的似然比统计量为χ²=25.707。

3. 确定P值，做出统计推断

统计量服从自由度为6 (两个分类变量哑变量个数之和)的χ²分布。由此可确定，P<0.001，即模型整体有统计学意义。

(二) 回归系数检验

对每个自变量的回归系数进行检验，即判断每个自变量对模型是否有贡献。常用的假设检验为Wald检验。

1. 建立假设检验，确定检验水准

H₀：β_ij=0

H₁：β_ij≠0

α=0.05

2. 计算检验统计量

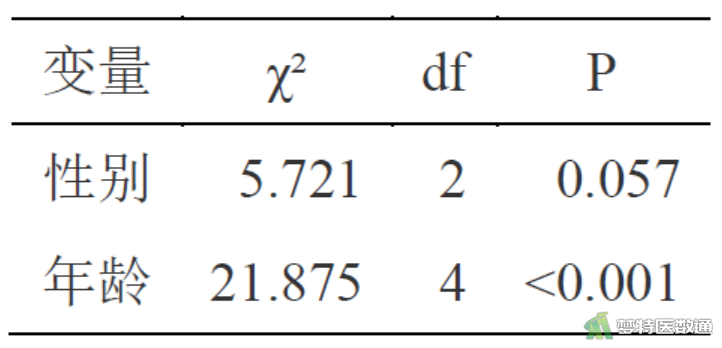
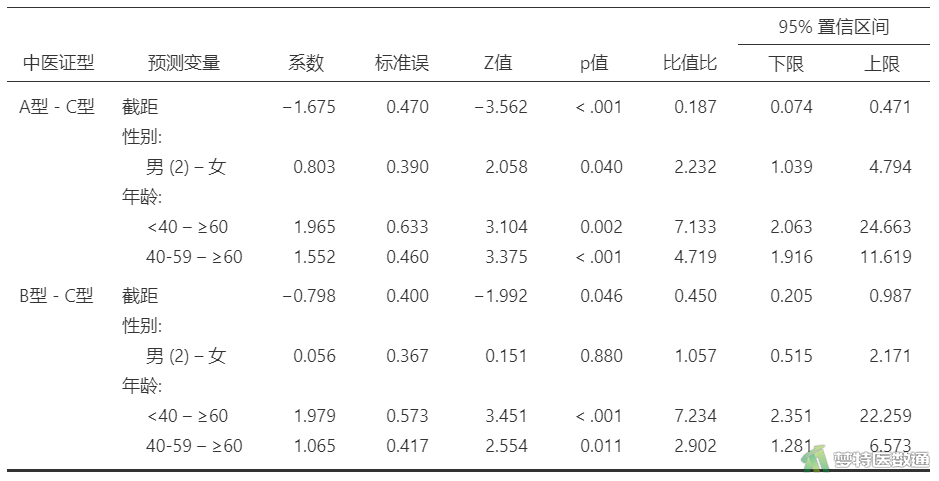
通过软件分析可得相关结果。详见图2、图3。

3. 确定P值，做出统计推断

由图2可知，性别(χ²=5.721，P=0.057)在模型中无统计学意义，年龄(χ²=21.875，P<0.001)在模型中有统计学意义，是中医证型的影响因素。

在“中医证型”A与C比较中，性别的P=0.040，但这并不能表示性别在模型中具有统计学意义，因为该变量的整体检验并无统计学意义(图2)。年龄<40岁的患者和年龄40-59岁的患者出现C型的风险分别是≥60岁患者低的7.133倍 (95%CI：2.063~24.664；P=0.002和4.719倍(95%CI：1.916~11.619；P<0.001)。

在“中医证型”B与C的比较中，性别同样无统计学意义。年龄<40岁的患者出现B型的风险是年龄≥60岁的7.234倍 (95%CI：2.351~22.260；P<0.001)，年龄40-59岁的患者出现B型的风险是年龄≥60岁的2.902倍 (95%CI：1.281~6.573；P=0.011)。

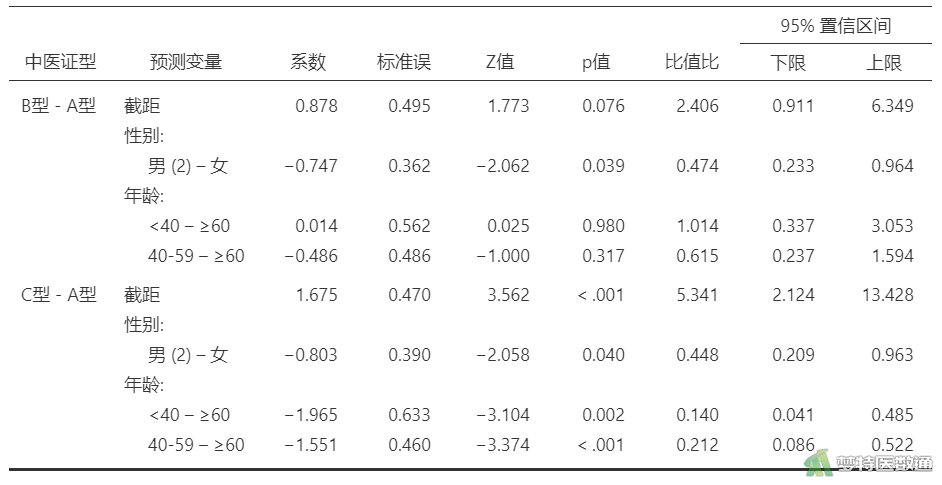
上述分析是以因变量C水平为参照得出的分析结果，可知A与C、B与C相比的情况，但是不知道B与A相比的情况。此处以水平A为参照进行分析。结果如图4所示。

由图4可知，在“中医证型”B与A比较中，性别的P=0.039，但这并不能表示性别在模型中具有统计学意义，因为该变量的整体检验并无统计学意义(图2)。年龄<40岁的患者和年龄40-59岁的患者出现B型的风险与年龄≥60岁的患者相比，也均无统计学差异(P=0.980和P=0.317)。

C与A比较的结果等价于图3中A与C比较的结果。