条件Logistic回归分析(Condition Logistic Regression Analysis)——SAS软件实现

关键词：SAS; 条件logistic回归; 配对logistic回归; 条件逻辑回归; 配对逻辑回归

一、 案例介绍

某肾内科医师拟探究急性肾损伤的危险因素，回顾性收集了109例在院内发生急性肾损伤患者的性别、年龄、体质指数(BMI)、血肌酐(Cr)和血清乳酸(Serum Lactate)，并根据性别和年龄进行1:1配对，收集了109例未发生肾损伤患者的相关信息，进行配对病例对照研究。部分数据见图1。本文案例可从“附件下载”处下载。sAKI表示急性肾损伤发生情况(1=发生，0=未发生)；Gender表示性别(0=女，1=男)；Age表示年龄；BMI表示体质指数(1=偏瘦，2=中等，3=超重)；Cr表示血肌酐含量；Lactate表示血清乳酸含量；subclass表示对子数，配对的两位患者对子数相同。

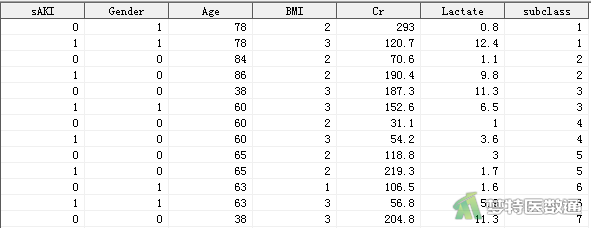
二、问题分析

本案例的分析目的是探讨某肾内科医师拟探究急性肾损伤的危险因素，采用配对设计，研究多个因素对二分类因变量的影响，可以采用条件logistic回归分析。但需要满足7个条件：

条件1：因变量为二分类变量。本研究中因变量为是否发生急性肾损伤“是”和“否”，为二分类变量，该条件满足。

条件2：至少有1个自变量。自变量可以是分类变量也可以是连续变量。本研究中有多个自变量，类型各异，该条件满足。

条件3：观察变量为配对设计。本研究中，两组患者是根据性别和年龄进行1:1配对，该条件满足。

条件4：因变量对子数为自变量个数的10~15倍(EPV原则)，最好＞30对，自变量的参照水平组不应少于30或50例。该条件需要通过软件分析后判断。

条件5：自变量之间无多重共线性。该条件需要通过软件分析后判断。

条件6：自变量不存在显著的异常值。该条件需要通过软件分析后判断。

条件7：数据未出现完全分离或拟完全分离现象。该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件4判断(因变量样本例数)

(1) SAS实现

首先导入数据，代码如下：

proc import datafile="G: \test\条件logistic回归.csv" dbms=csv out=data1;
run;

使用如下的proc freq过程步，统计因变量每类的样本例数。

proc freq data=data1;
	tables sAKI;
run;

(2) 结果解读

如图2所示，发生(sAKI=1)和未发生(sAKI=0)急性肾损伤的患者均为109例，根据“因变量对子数为自变量个数的10~15倍(EPV原则)”，本案例可纳入7~11个自变量进行多因素条件logistic回归分析。

2. 条件4判断(自变量样本例数)

(1) SAS实现

使用如下的proc freq过程步，统计分类变量BMI各类别的因变量例数。

proc freq data=data1;
	tables sAKI*BMI;
run;

(2) 结果解读

如图3所示，BMI水平为偏瘦(BMI=1)时，因变量的例数<30，如果该变量在多因素分析过程中进入模型，应注意避免例数较少的水平被选为参照。

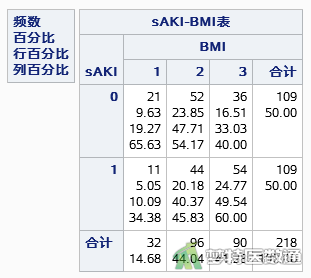
3. 条件5判断(多重共线性诊断)

(1) SAS实现

对进入模型的变量进行多重共线性诊断，代码如下所示：

首先对分类变量设置哑变量：

data data2;
	set data1;
	length BMI1 BMI2 8.;
	BMI1=ifc(BMI=1,1,0);
	BMI2=ifc(BMI=2,1,0);
run;

使用线性回归过程步进行多重共线性诊断：

proc reg data=data2;	
	model sAKI={BMI1 BMI2} Cr Lactate/tol vif;
quit;

(2) 结果解读

如图4所示，所有自变量的方差膨胀因子均<5，容忍度均>0.1，提示自变量之间不存在严重共线性问题。

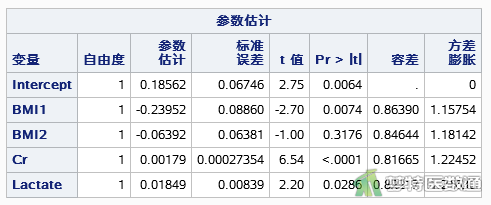
4. 条件6判断(异常值检测)

(1) SAS实现

使用reg过程步计算Cook距离，代码如下：

proc reg data=data2;	
	model sAKI={BMI1 BMI2} Cr Lactate/r;
quit;

(2) 结果解读

如图5所示，最大的库克距离值为0.336<0.5，提示不存在显著异常值，本研究数据满足条件6。

5. 条件7判断(完全分离检测)

完全分离，指存在一个自变量或自变量的线性组合，能够正确分配所有的样本点到其相应的因变量分组，此时，最大似然估计值不存在，常表现为OR值无穷大。对于分类变量，完全分离表现为分类变量和因变量的四格表中出现0，如图3所示，四格表中未出现0，因此BMI不存在完全分离现象。本研究数据满足条件7。

(二) 模型拟合

1. SAS实现

SAS实现条件logistic回归有两种方法，第一种是proc logistic过程步，代码如下所示：

proc logistic data=data1 descending ;	
	class BMI(param=reference ref="3");
	model sAKI=BMI Cr Lactate/stb rsquare;
	strata subclass;
quit;

SAS默认因变量的较小值与较大值进行比较，在本例中，发生肾损伤为1、未发生肾损伤为0，本案例研究目的是探讨发生肾损伤的主要影响因素，因此使用descending选项将其反转。class选项对分类变量设置参照，本例以 BMI超重为参照。stb选项输出标准回归系数。rsquare选项输出模型R²的值。strata subclass设置对子数为分层因素。

SAS提供了另一种实现条件logistic回归的方法，代码如下所示：

data data3;
	set data1;
	t=1-sAKI;
run;
proc phreg data=data3;
	class BMI(param=reference ref="3");
	model t*sAKI(0)=BMI Cr Lactate/ties=discrete risklimits;
	strata subclass;
quit;

首先生成虚拟生存时间t，此处生成的虚拟生存时间要保证对照组数值大于病例组，即虚拟的生存时间对照组比病例组长，本案例使用1-sAKI，也可以选用其他数值减去sAKI。

proc phreg是专门用于做生存分析的过程步，其中model语句等号左边分别是生存时间*生存状态，生存状态后在括号中列出代表失访或存活的截尾值赋值，在本案例中我们生成了虚拟生存时间t，并以未发生肾损伤(sAKI=0)作为生存状态，因此model等号左边为t*sAKI(0)，等号右边是所有自变量。ties=discrete表示建立离散的logistic回归，risklimits给出参数估计的95%置信区间。strata subclass设置对子数为分层因素。

2. 结果解读

(1) 拟合优度

使用proc logistic和proc phreg过程步进行条件logistic回归分析的结果一致，因此，下文以proc logistic的输出结果为例进行展示。

如图6所示，模型(不带协变量)AIC 、SC和-2 Log L值均为151.106，模型(带协变量)AIC 、SC和-2 Log L值分别为92.806、106.344、84.806。模型R²值为0.2622，最大重新换算R²值为0.5245，R²值越接近1表明模型拟合度越高，因此表明本数据集模型拟合度一般。似然比检验χ²=66.2996，P<0.0001，表明模型有统计学意义。

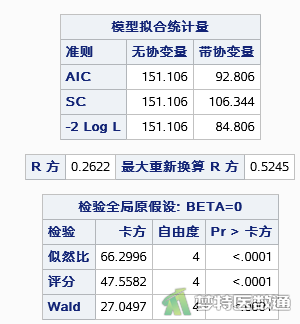
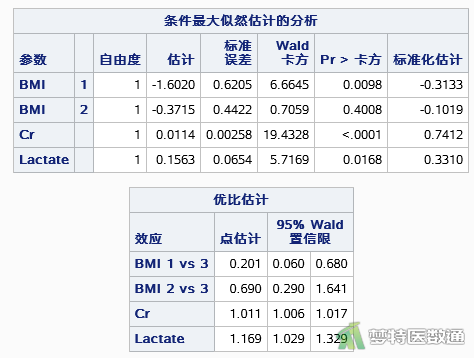
(2) 模型系数

如图7所示，BMI偏瘦和超重相比，偏瘦发生急性肾损伤的风险是超重的0.201倍 (95%CI：0.060~0.680；P=0.0098)，BMI中等和BMI超重之间的差异无统计学意义(P=0.4008>0.05)。血肌酐Cr点估计值为1.011，大于1，说明急性肾损伤风险随着血肌酐Cr的增高而增加，具体解释为血肌酐Cr每增高一个单位，发生急性肾损伤的风险增加0.011倍 (95%CI：0.006~0.017；P<0.001)；血清乳酸Lacate的点估计值为1.169，大于1，说明急性肾损伤风险随着血清乳酸Lacate的增高而增加，具体解释为血清乳酸Lacate每增高一个单位，发生急性肾损伤的风险增加0.169倍 (95%CI：0.029~0.329；P=0.0168)。

四、结论

本研究采用条件Logistic回归探讨急性肾损伤的危险因素。因变量对子数和自变量个数满足需求，变量之间不存在严重共线性和异常值，数据不存在完全分离现象。

三个自变量经过分析后发现均有统计学意义，其中BMI偏瘦发生急性肾损伤的风险是超重的0.201倍 (95%CI：0.060~0.680；P=0.0098)；急性肾损伤风险随着血肌酐Cr的增高而增加，血肌酐Cr每增高一个单位发生风险增加0.011倍 (95%CI：0.006~0.017；P<0.001)；急性肾损伤风险随着血清乳酸Lacate的增高而增加，血清乳酸Lacate每增高一个单位发生风险增加0.169倍 (95%CI：0.029~0.329；P=0.0168)。所建立的模型有统计学意义(似然比检验χ²=66.2996，P<0.0001)。