有序Logistic回归分析(Ordinal Logistic Regression Analysis)——SAS软件实现

关键词：SAS; 有序logistic回归; 有序逻辑回归; 平行性检验; 比例优势检验

一、案例介绍

在某胃癌筛查项目中，为了确定胃癌筛查的重点人群，研究者想了解首诊“胃癌分期(Stage：0=I-II期，2=III期，3=IV期，4=V期)”与患者“经济水平(Income：1=低收入，2=中等收入，3=高收入)”、“性别(Gender：0=女，1=男)”和“年龄(Age)”之间的关系，试对数据进行分析。部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是探讨首诊“胃癌分期”与患者“经济水平”、“性别(Gender)”和“年龄(Age)”之间的关系。在案例中，首诊“胃癌分期”为因变量，有I-II期、III期、IV期、V期4个分类，且分类间有等级次序关系。因此，可以采用有序logistic回归模型进行分析。但需要满足以下5个条件：

条件1：因变量唯一，且为有序多分类变量。本研究中因变量只有“胃癌分期”，且为有序多分类变量，该条件满足。

条件2：存在一个或多个自变量。本研究中有三个自变量，“性别”和“经济水平”为分类变量，“年龄”为连续变量，该条件满足。

条件3：观察变量相互独立。本研究中各研究对象的观察变量都是独立的，不存在互相干扰的情况，该条件满足。

条件4：自变量之间无多重共线性，该条件需要通过软件分析后判断。

条件5：满足平行性，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

①利用LIBNAME语句建立SAS逻辑库关联，注意逻辑库名称要求，即最大长度8字符，必须以字母或下划线“_”开始，可以是字母、数字和下划线的任意组合。具体代码如下：

libname mydata 'D:\mydata';

通过这一步骤，SAS能够识别引号中的物理位置，将逻辑库建立在该目录下，同时在以下过程中新建的SAS表格便可以永久储存在该位置，便于反复读取和使用。先运行该代码使其生效。

②利用PROC IMPORT语句导入文件，代码如下：

proc import out= mydata.example
datafile=" D:\mydata\有序Logistic回归分析.csv"
dbms=csv replace;
getnames=yes;
run;

该过程在mydata逻辑库中生成example数据集，数据文件由DATAFILE=选项指定，DBMS=选项指定其数据库类型。该案例中初始数据集为csv文件，故而使用“dbms=csv”指定。如果已经存在相同名称的SAS数据集，即可使用REPLACE选项进行覆盖。GERNAMES=YES选项指定从第2行开始读取数据，将数据集的首行变量名作为SAS数据集的变量名。

(二) 适用条件判断

1. 条件4判断(多重共线性判断)

(1) 软件操作

首先对多分类变量设置哑变量：

data mydata.example2;
	set mydata.example;
	length Income1 Income2 8.;
	Income1=ifc(Income=2,1,0);
	Income2=ifc(Income=3,1,0);
run;

使用线性回归过程步进行多重共线性诊断：

proc reg data= mydata.example2;
	model Stage = Gender Age {Income1 Income2} / tol vif;
quit;

(2) 结果解读

如图2所示，所有自变量的方差膨胀因子均<10，容忍度均>0.1，提示自变量之间不存在严重共线性问题，满足分析条件。若存在严重多重共线性，处理方法参照多因素二分类logistic回归。

2. 条件5判断(平行性检验)

(1) 软件操作

①运用LOGISTIC过程进行检验，具体代码如下：

proc logistic data = mydata.example descending ; 
class Gender Income (ref=first)/param=ref;
model Stage = Gender Age Income /LINK=clogit;
run;

DESCENDING选项将Stage=1 (I-II期)作为参照组。CLASS语句指定将“Gender”和“Income”作为分类变量进行分析，“ref=first”将Gender=0和Income=1作为参照组。该步骤中MODEL语句将“Stage”作为因变量，将“Gender” “Age”和“Income”变量纳入模型。“LINK=clogit”选项进行平行性检验。

(2) 结果解读

图3展示了模型的平行性检验，平行性检验的原假设是各回归方程互相平行，χ²=3.2102，P=0.9205>0.05接受原假设，说明平行性假设成立，即各回归方程相互平行，满足条件5。

(三) 变量筛选

(1) 软件操作

①运用LOGISTIC过程进行变量筛选，此过程与上一步骤中相似，但不需加入“LINK=clogit”选项。具体代码如下：

proc logistic data = mydata.example descending ; 
class Gender Income (ref=first)/param=ref;
model Stage = Gender Age Income ;
run;

②相同步骤中，在MODEL语句中可以加入STEPWISE或BACKWARD选项，对单个变量在模型中的影响进行检验。示例代码如下：

proc logistic data = mydata.example descending ; 
class Gender Income (ref=first)/param=ref;
model Stage = Gender Age Income / stepwise;
run;
proc logistic data = mydata.example descending ; 
 class Gender Income (ref=first)/param=ref;
 model Stage = Gender Age Income / backward;
run;

(2) 结果解读

图4中“Testing Global Null Hypothesis (检验模型原假设)”显示了整体模型的检验结果，可见模型有统计学意义，说明模型中至少存在一个自变量具有统计学意义。

图5中“Type 3 Analysis of Effects (类型3效应分析)”中列出了每个自变量在模型中是否有统计学意义，即是否应被纳入模型。可知，“Gender (性别)”无统计学意义，可被移除模型。

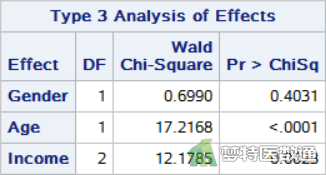
图6是由stepwise选项得出的结果，由“Summary of Stepwise Selection (逐步筛选总结)”可见最终纳入模型的自变量为“Age”和“Income”。

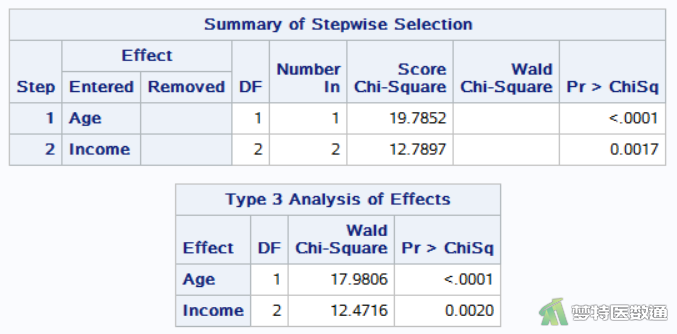
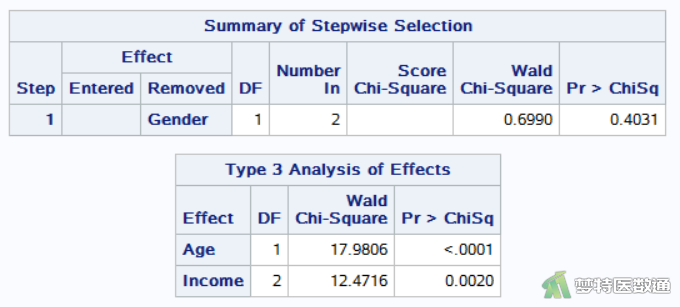
图7是由backward选项得出的结果，由“Summary of Stepwise Selection (逐步筛选总结)”可见最终排除出模型的自变量为“Gender”。

(四) 模型拟合

1. 软件操作

①上一步骤中加入STEPWISE或BACKWARD选项的LOGISTIC过程即可得到拟合结果。

②也可另用LOGISTIC过程，仅将“Age”和“Income”加入自变量。具体代码如下：

proc logistic data = mydata.example descending ; 
class Income(ref=first)/param=ref;
model Stage = Age Income;
run;

2. 结果解读

(1) 拟合优度

图8“Model Fit Statistics (模型拟合度量)”结果，列出了模型的 “AIC (赤池信息量准则)”等信息和“Testing Global Null Hypothesis (检验模型原假设)”。

AIC是衡量统计模型拟合优良性(Goodness of fit)的一种标准，其值越小越好，因此本数据集模型拟合度不高。“Testing Global Null Hypothesis (检验模型原假设)”采用的是似然比卡方检验对模型进行参数检验，考察模型的整体显著性，可见整体模型有统计学意义。

(2) 模型系数

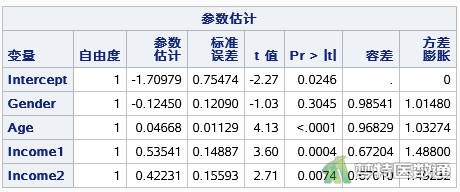
从图9“Type 3 Analysis of Effects (类型3效应分析)”可见，“Age”和“Income”两个自变量均有统计学意义。

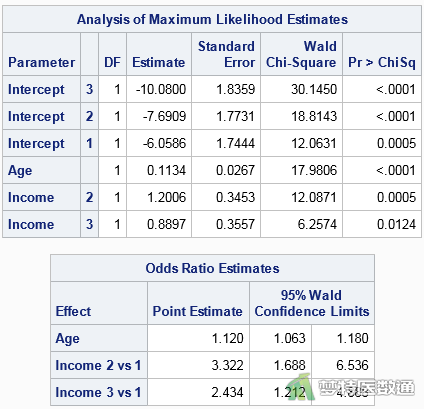
图10“Analysis of Maximum Likelihood Estimates (最大似然比分析)”表格列出了各自变量拟合后在模型中的“Estimate(回归系数)”、“Standard Error (标准误)”、“Wald Chi-Square (统计量)”、“Pr (P值)”。“Odds Ratio Estimates (比值比估计)”表中给出了“Point Estimate (点估计)”及其95%CI。

其中“年龄”的P<0.0001，有统计学意义；OR=1.120 (95%CI：1.063~1.180)，表示年龄每增加一岁，其首诊“胃癌分期”提升一个等级的可能性是原来的1.120倍。“中等收入”水平患者首诊“胃癌分期”提升一个等级的可能性是“低收入”水平患者的3.322倍(95%CI：1.688~6.536，P=0.0005)；“高收入”水平患者首诊“胃癌分期”提升一个等级的可能性是“低收入”水平患者的2.434倍(95%CI：1.212~4.888，P=0.0124)。

四、结论

本研究采用有序logistic回归模型分析首诊“胃癌分期”与患者“经济水平”、“性别”和“年龄”之间的关系。因变量例数分布满足样本量需求，变量之间不存在严重共线性，满足平行性假设(χ²=3.2102，P=0.9205)。

“性别”对首诊“胃癌分期”的影响无统计学意义。“年龄”每增加一岁，其首诊“胃癌分期”提升一个等级的可能性是原来的1.120倍 (95%CI：1.063~1.180，P<0.0001)。“中等收入”水平患者首诊“胃癌分期”提升一个等级的可能性是“低收入”水平患者的3.322倍(95%CI：1.688~6.536，P=0.0005)；“高收入”水平患者首诊“胃癌分期”提升一个等级的可能性是“低收入”水平患者的2.434倍(95%CI：1.212~4.888，P=0.0124)。所建立的模型有统计学意义(χ²=35.2916，P<0.0001)。

五、知识小贴士

• 有序logistic回归模型分析结果除了常数项不同，各模型的自变量系数都相同。平行性检验的目的即是验证自变量不同取值对因变量的影响系数是否相同，即要满足无论因变量的分割点在什么位置，模型中各个自变量对因变量的影响不变。
• 如果不满足平行性假设，则考虑使用无序多分类logistic回归或用不同的分割点将因变量变为二分类变量，分别进行二项logistic回归。但是，当样本量过大时，平行线检验会过于敏感。即当存在平行性时，也会显示P<0.05。此时，可以尝试将因变量设置为哑变量，并拟合多个二项logistic回归模型，通过观察自变量对各哑变量的OR值是否近似来判断。