在二分类logistic回归的理论篇中,介绍了可用于成组病例对照研究的非条件logistic回归。而对于配对设计的病例对照研究,一般使用倾向性评分等方式将病例组和对照组进行1:n (n=1、2、3、4、…、n)的配对,以消除某些(可疑)混杂因素的影响,从而探究特定因素与结局的关联。在这里,病例和对照是成对出现的,不宜使用非条件logistic回归,需要用条件logistic回归。本篇文章将举例介绍条件logistic回归的假设检验理论。
关键词:条件logistic回归; 配对logistic回归; 条件逻辑回归; 配对逻辑回归
一、基本概念
在配对的数据中,病例和对照会成对存在,如1个病例匹配1个或多个对照。设有n个匹配组(每一组可视为一个层),每一组的第一个观察对象为病例,另有m个对照,用Xitj表示第i组第t个观察对象的第j个影响因素对应的观察值。
若用Pi表示第i层在m个影响因素作用下的发病概率,那么条件logistic模型可表示为
\(P_{i}=\frac{1}{1+e^{\left[-\left(\beta_{0 i}+\beta_{1}X_{1}+\beta_{2} X_{2}+\cdots+\beta_{m}X_{m}\right)\right]}}\)
β0i表示各匹配组的效应,不同匹配组的数值可以不同,但假定其相同;β1、β2、β3等表示被估计的总体参数。
二、适用条件
条件logistic回归需要满足以下6个条件:
条件1:因变量为二分类变量。
条件2:至少有1个自变量,可以是分类变量,也可以是连续变量。
条件3:因变量的观察结果为配对设计或具有相关性,即不满足独立性。
条件4:因变量对子数为自变量个数的10~15倍(EPV原则),最好>30对,自变量的参照水平组不应少于30或50例。
条件5:自变量之间无多重共线性。
条件6:自变量不存在明显的异常值。
三、参数估计
在第i个匹配组中M+1个观察对象有1个病例的条件下,恰好第一个观察对象为病例的条件概率,即条件似然函数为:
\(L_{i}=\frac{P\left(X_{i 0} \mid Y=1\right)\prod_{t=1}^{M} P\left(X_{i t} \mid Y=0\right)}{\sum_{t=0}^{M}\left[P\left(X_{i t} \mid Y=1\right) \prod_{t=0}^{M}{ }_{t \neq t} P\left(X_{i t}\mid Y=0\right)\right.}\)
这等于观察到的第一组影响因素属于病例的概率与各种可能组合情况的概率比值。由条件似然函数和模型公式可知:
\(L_{i}=\frac{1}{1+\sum_{t=1}^{M} \exp\left[\sum_{t=1}^{M} \beta_{j}\left(X_{i t j}-X_{i 0j}\right)\right]}\)
那么,综合n个匹配组的条件似然函数为:
\(\mathrm{L}=\prod_{i=1}^{n} \frac{1}{1+\sum_{t=1}^{M} \exp \left[\sum_{j=1}^{m} \beta_{j}\left(X_{i t j}-X_{i 0 j}\right)\right]}\)
由上述公式可以看出,条件logistic 回归分析只需要估计影响因素的回归系数βj,而各匹配组(层)的效应β0i已经被消去。
对上述条件似然函数L取自然对数后,可用Newton - Raphson 迭代方法求得参数的估计值bj及其标准误\(S_{b_{j}}\)。具体分析方法与非条件logistic 回归完全相同。
四、假设检验
条件logistic回归的假设检验与非条件logistic回归一样,均是假设模型以及各个影响因素对应的回归系数是否有统计学意义。
五、案例分析
某肾内科医师拟探究急性肾损伤的危险因素,回顾性收集了109例在院内发生急性肾损伤患者的性别、年龄、体质指数(BMI)、血肌酐(Cr)和血清乳酸(Serum Lactate),并根据性别和年龄进行1:1配对,收集了109例未发生肾损伤患者的相关信息,进行配对病例对照研究。部分数据见图1。
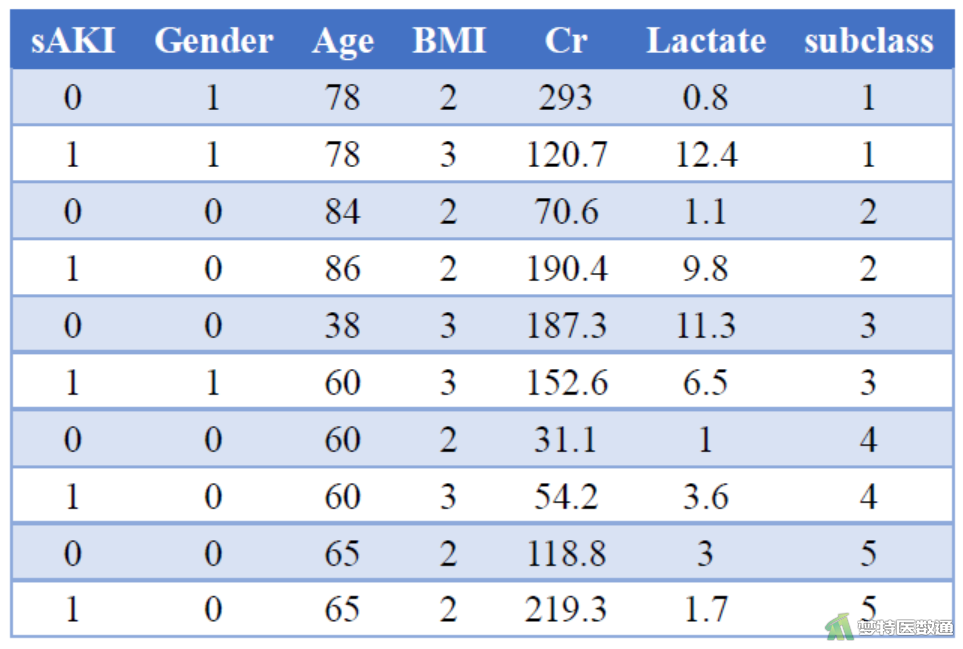
将BMI、Cr和Lactate纳入模型中借助软件进行分析。对于本案例数据,连续性自变量加上分类变量的哑变量,共有4个自变量。通过软件分析可得到条件logistic回归模型的整体检验以及每个变量对应的回归系数和标准误等参数。
图2是模型整体检验结果,可见条件似然函数的统计量为χ²=47.558,P<0.001,说明模型有统计学意义,即模型中至少有一个自变量有统计学意义。
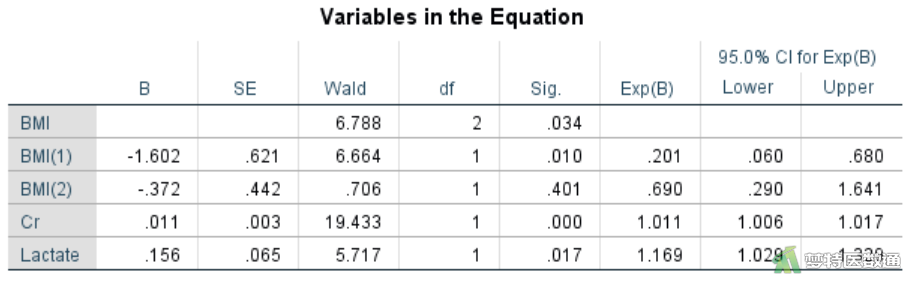
图3给出了各个自变量的Wald值、P值和对应的效应量OR值及其95%CI。可知BMI (P=0.034)、Cr(P<0.001)和Lactate (P=0.017)在模型中均有统计学意义。其中BMI偏瘦发生急性肾损伤的风险是超重的0.201倍 (95%CI:0.060~0.680;P=0.010);急性肾损伤风险随着Cr的增高而增加,Cr每增高一个单位发生风险增加0.011倍 (95%CI:0.006~0.017;P<0.001);急性肾损伤风险随着Lacate的增高而增加,Lacate每增高一个单位发生风险增加0.169倍 (95%CI:0.029~0.329;P=0.017)。
