配对样本t检验(Paired Samples t-test)——R软件实现

关键词：R语言; R软件; t检验; 配对样本t检验; 配对t检验; 成对t检验; 成组t检验; 关联样本t检验; 差值正态性

一、案例介绍

为检测肌肉组织中某生化指标(X)的含量，分别使用A、B两种方法检测17只小白鼠肌肉组织中该生化指标(X)的含量，试问两种方法检测的结果是否有差异。部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是比较两种检测方法对同一批样本检测的结果是否存在差异，由于检测的指标是计量资料，因此可以使用配对样本t检验。但需要满足5个条件：

条件1：观察变量为连续变量。本研究中的生化指标(X)含量为连续变量，该条件满足。

条件2：观察变量为配对设计。本研究中，两组数据均是对同一批研究对象测量所得，因此属于配对样本。该条件满足。

条件3：观察变量可分为2组，本研究中分为A方法和B方法两组，该条件满足。

条件4：观察变量不存在显著的异常值，该条件需要通过软件分析后判断。

条件5：两个配对组别间观察变量的差值服从正态(或近似正态)分布，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 导入数据

mydata<-read.csv("配对样本T检验.csv")  #导入CSV数据
View(mydata)  #查看数据

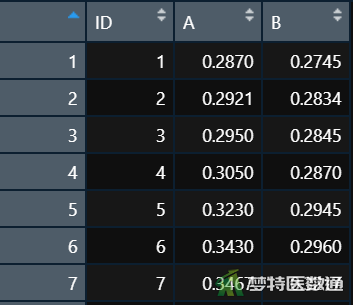
在数据栏目中可以查看全部数据情况，数据集中共有3个变量和17个观察数据，3个变量分别代表被调查者的编号(ID) 、A方法(A)及B方法(B)。
如果数据集较大也可使用如下命令查看数据框结构：

str(mydata) #查看数据框结构

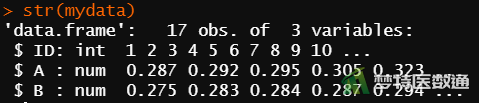
(二) 适用条件判断

1. 条件4判断(异常值判断)

(1) 软件操作

##查看最大值和最小值##

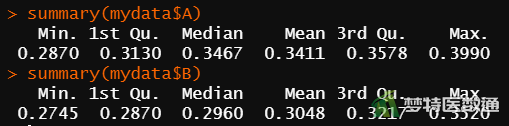
summary(mydata$A)  #描述A方法的基本情况
summary(mydata$B)  #描述B方法的基本情况

##查看缺失值情况##

is.na(mydata$A)  #查看A方法是否存在缺失值
is.na(mydata$B)  #查看B方法是否存在缺失值 

##分组绘制箱线图##

par(mfrow = c(1, 2))  #设置画1行2个图片
boxplot(mydata$A, xlab = "A方法", ylab = "X")  #绘制A方法的箱线图
boxplot(mydata$B, xlab = "B方法", ylab = "X")  #绘制B方法的箱线图

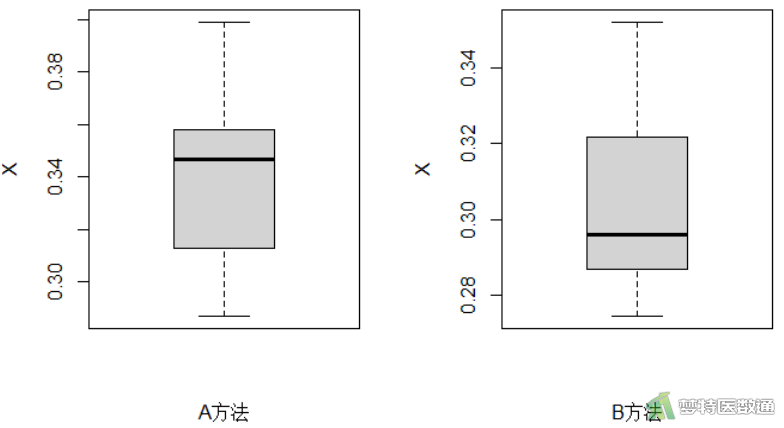
(2) 结果解读

图3“summary (描述性分析)”命令运行结果，列出了观察变量的“Min(最小值)”、“1st Qu(P25)”、“Median(中位数)”、“Mean(平均值)”、“3rd Qu(P75)”和“Max(最大值)”，最小值和最大值分别为0.275和0.399，尚无专业依据认定为异常值；此外，图5中的箱线图也未提示任何异常值。综上，本案例未发现需要删除的异常值，满足条件4。

2. 条件5判断(正态性检验)

(1) 软件操作

##绘制Q-Q图##

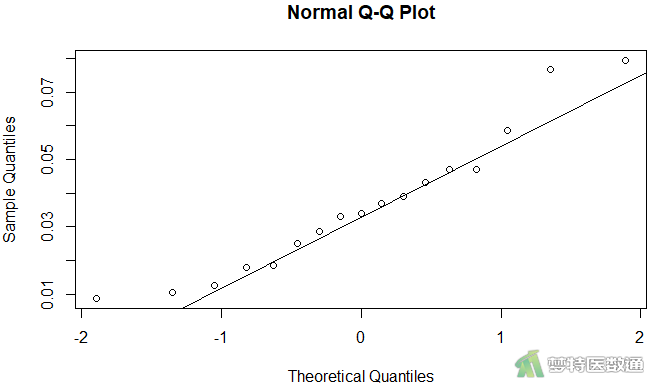
d <- mydata$A - mydata$B  #计算两组间差值
qqnorm(d)  #绘制Q-Q图
qqline(d)  #增加趋势线

##正态性检验##

shapiro.test(d) #shapiro-Wilk正态性检验

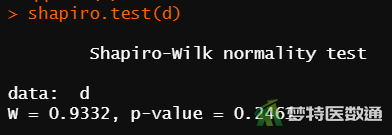
(2) 结果解读

图6 Q-Q图上散点基本围绕对角线分布，提示数据呈正态分布；图7的“Shapiro-Wilk normality test (S-W正态性检验)”表格结果显示P=0.2461>0.1，也提示数据服从正态分布。综上，本案例满足条件5。关于正态性检验的注意事项详见医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现。

 (三) 统计描述及推断

1. 软件操作

##描述性分析##

install.packages("psych")  #安装程序包“psych”
library(psych)  #调用程序包“psych”
describe(mydata$A)  #描述A方法的集中和离散趋势
describe(mydata$B)  #描述B方法的集中和离散趋势

##配对样本t检验##

t.test(mydata$A,mydata$B,paired = TRUE)

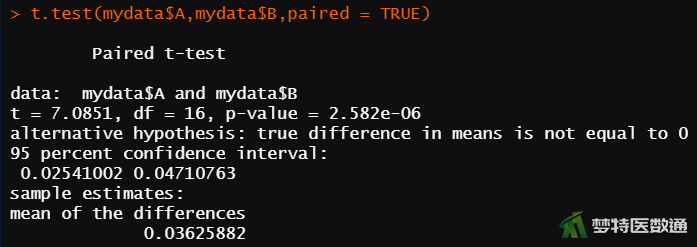
2. 结果解读

(1) 统计描述

图8“describe (描述性分析)”的结果提供了研究案例的“mean(均数)”和“sd(标准差)。可知，A方法组含量为0.341±0.035，B方法组含量为0.305±0.023，图5为两种方法检测的生化指标(X)含量的分布图。两组检测结果貌似存在差异，但还需要依据统计学检验的结果进行判断。

(2) 统计学推断

图9“Paired t-test (配对样本t检验)”运行结果中提供了统计学推断后的“t (统计量t)”、“df (自由度)”、“p-value (P值)”、推断结果、“mean of the differences(差值的均值)”及“95 percent confidence interval (95%可信区间，95%CI)”。 可知A方法检测结果比B方法平均高0.036，95%CI为0.025~0.047；差异有统计学意义(t=7.0851，P<0.001)。

(四) 相关性检验

1. 软件操作

##绘制回归线散点图##

plot(mydata$A, mydata$B, xlab = "A", ylab = "B")  #绘制散点图
abline(lm(mydata$B ~ mydata$A))  #添加回归线

cor.test(mydata$A,mydata$B,method="pearson") #相关性检验

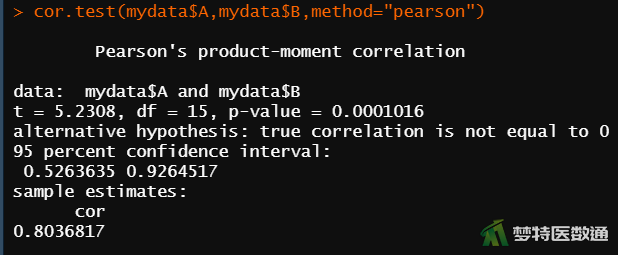
##绘制相关性检验结果的散点回归线图##

library(ggplot2)  #启用程序包“ggplot2”
library(ggpubr)  #启用程序包“ggpubr”
ggplot(data = mydata, aes(x=mydata$A,y=mydata$B)) +
  geom_point(color="red") +
  stat_smooth(method="lm",se=TRUE) + 
  stat_cor(data=mydata, method = "pearson")  #绘制相关性检验结果的散点回归线图

2. 结果解读

图10的散点图提示，两组之间存在线性相关。图11“cor.test (相关性分析)”分析结果可知，两组Pearson相关系数r = 0.8036817(图11最后一行)，P < 0.001，提示两组数据之间存在相关性，表明A、B两种方法之间的差异具有较好的稳定性，满足条件6。图12为在图中标记相关性检验结果的散点图，显示更为直观，可以选择性使用。

相关性的计算是为了验证配对数据的一致性，可以说明研究因素作用的稳定性或一致性，可能存在四种情况。①相关性检验与配对t检验的P值均<0.05，说明数据一致性较好，差异有统计学意义，而且差异的产生就是研究因素作用的结果。②相关性检验P>0.05，配对t检验的P<0.05，说明两组数据间存在差异，但对子间均数差异变化不一致，均数差异可能还受其他因素的影响。③相关性检验P<0.05，但配对t检验的P>0.05，说明数据变化有一致性，但均数差异不显著，即研究因素未发挥作用。④相关性检验与配对t检验的P值均>0.05，说明数据在两组间不具备一致性，且差异也无统计学意义。本案例为第①种情况。

四、结论

本研究采用配对样本t检验判断A、B两种方法检测肌肉组织中生化指标(X)的含量是否有差异。通过专业知识判断，数据不存在需要删除的异常值；通过绘制Q-Q图和Shapiro-Wilk检验，提示两组数据差值满足正态分布。

结果显示，A、B方法检测肌肉组织中生化指标(X)的含量分别为0.341±0.035和0.305±0.023，A方法平均值比B方法高0.036 (95%CI：0.025~0.047)，差异有统计学意义(t=7.085，P<0.001)。两组Pearson相关系数r = 0.804，P < 0.001；表明A、B两种方法之间的差异具有较好的稳定性。因此，本案例分析表明，使用A方法检测肌肉组织中生化指标(X)的含量通常会比B方法检测结果值要高。