配对样本t检验(Paired Samples t-test)——SAS软件实现

关键词：SAS; t检验; 配对样本t检验; 配对t检验; 成对t检验; 成组t检验; 关联样本t检验; 差值正态性

一、案例介绍

为检测肌肉组织中某生化指标(X)的含量，分别使用A、B两种方法检测17只小白鼠肌肉组织中该生化指标(X)的含量，试问两种方法检测的结果是否有差异？部分数据见图1(A方法为group1，B方法为group2)。本文案例可从“附件下载”处下载。

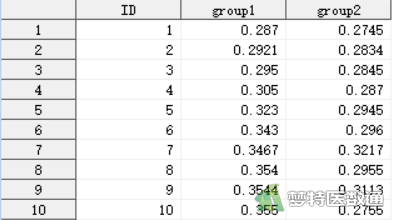
二、问题分析

本案例的分析目的是比较两种检测方法对同一批样本检测的结果是否存在差异，由于检测的指标是计量资料，因此可以使用配对样本t检验。但需要满足5个条件：

条件1：观察变量为连续变量。本研究中的生化指标(X)含量为连续变量，该条件满足。

条件2：观察变量为配对设计。本研究中，两组数据均是对同一批研究对象测量所得，因此属于配对样本。该条件满足。

条件3：观察变量可分为2组，本研究中分为A方法和B方法两组，该条件满足。

条件4：观察变量不存在显著的异常值，该条件需要通过软件分析后判断。

条件5：两个配对组别间观察变量的差值服从正态(或近似正态)分布，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一)导入数据

①利用LIBNAME语句建立SAS逻辑库关联，注意逻辑库名称要求，即最大长度8字符，必须以字母或下划线“_”开始，可以是字母、数字和下划线的任意组合。具体代码如下：

libname mydata ‘D:\mydata’;

通过这一步骤，SAS能够识别引号中的物理位置，将逻辑库建立在该目录下，同时在以下过程中新建的SAS表格便可以永久储存在该位置，便于反复读取和使用。先运行该代码使其生效。

②利用PROC IMPORT语句导入文件，代码如下：

proc import out= mydata.example
    datafile=" D:\mydata\配对样本T检验.csv"
	  dbms=csv replace;
	  getnames=yes;
run;

该过程在mydata逻辑库中生成example数据集，数据文件由DATAFILE=选项指定，DBMS=选项指定其数据库类型。该案例中初始数据集为csv文件，故而使用“dbms=csv”指定。如果已经存在相同名称的SAS数据集，即可使用REPLACE选项进行覆盖。GERNAMES=YES选项指定从第2行开始读取数据，将数据集的首行变量名作为SAS数据集的变量名。

(二)适用条件判断

1. 条件4判断(异常值判断)

(1)软件操作

运用UNIVARIATE过程进行检验：

proc univariate data= mydata.example plot;
var group1 group2;
run;

其中“mydata.example”为上一步中导入的数据集名称，“group1”、“group2”为分析变量名，即分别为A方法和B方法检测的小白鼠肌肉组织中该生化指标(X)的含量。选项PLOT产生了两组(“group1”、“group2”)的平行条状图、箱线图和正态概率图，分别如图2、图3所示。

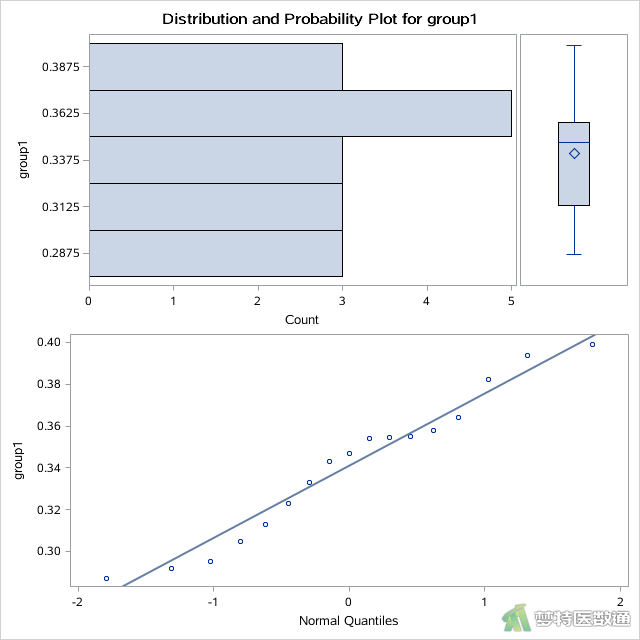
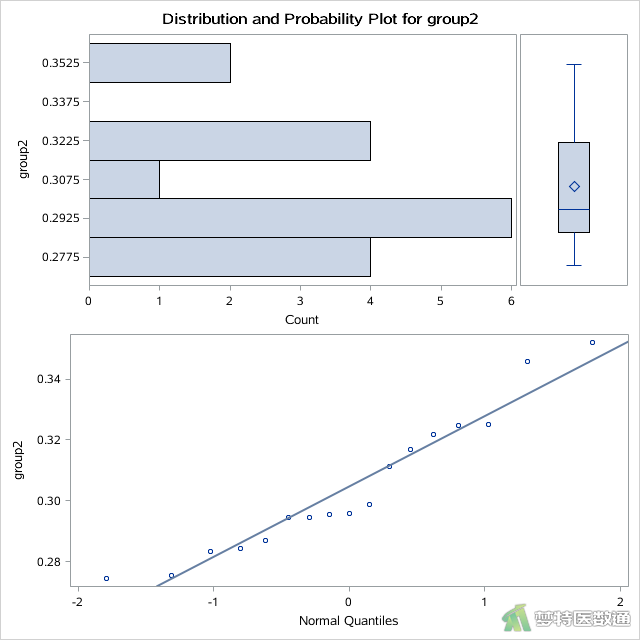
(2)结果解读

图4列出了组1 (“group1”)观察变量的“0% Min (最小值)”、“100% Max (最大值)”和其他“Quantiles (百分位数)”，由此可见组1(“group1”)的观察变量的最小值和最大值分别为0.2870和0.3990，尚无专业依据为异常值。

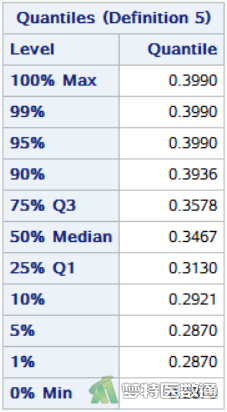
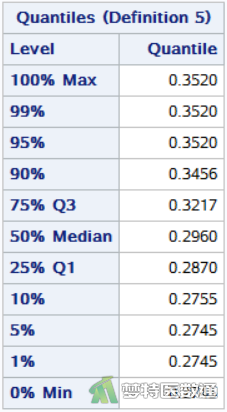
图5列出了组2 (“group2”)观察变量的“0% Min (最小值)”、“100% Max (最大值)”和其他“Quantiles (百分位数)”，由此可见组2(“group2”)观察变量的最小值和最大值分别为0.2745和0.3520。综上，两组数据的最大值和最小值依据专业判断均非异常值。

此外，图2和图3中组1 (“group1”)和组2 (“group2”)的平行条状图，箱线图和正态概率图，根据图形判断，也未发现任何异常值和极端值。综上，本案例未发现需要删除的异常值，满足条件4。

2. 条件5判断(正态性检验)

(1)软件操作

①用DATA过程计算两组差值，并命名为“difference”，示例代码如下：

data mydata.difference;
  set mydata.example;
  difference=group1-group2;
run;

该过程中新建表格，命名为“mydata.difference”，并用SET语句选择了原表格“mydata.example”，添加变量“difference”，其值为两组的差值，即A和B两种方法检测的小白鼠肌肉组织中该生化指标(X)的差值。“mydata.difference”表格中部分数据如图6所示：

②运用UNIVARIATE 过程对两组差值进行正态性检验，示例代码如下：

proc univariate data= mydata.difference normal;
var difference;
run;

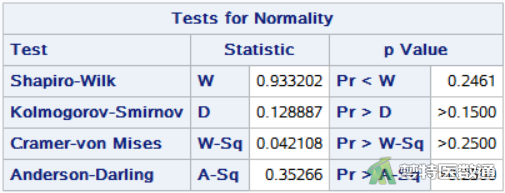
该步骤中对差值进行正态性检验，以上一步骤中所得“mydata.difference”表中的两组差值结果“difference”为研究对象，加入选项NORMAL进行正态性检验，得到“Normality Test (Shapiro-Wilk) (夏皮罗-威尔克正态性)”检验结果，如图7所示。

③运用TTEST过程得出直方图和Q-Q图：

proc ttest data= mydata.example;
  paired group1*group2;
run;

该步骤中运用原表格“mydata.example”，PAIRED 语句指定了进行配对分组的变量group1和group2，再继续按配对的差值时是“*”左侧变量减去“*”右侧变量，即group1-group2。

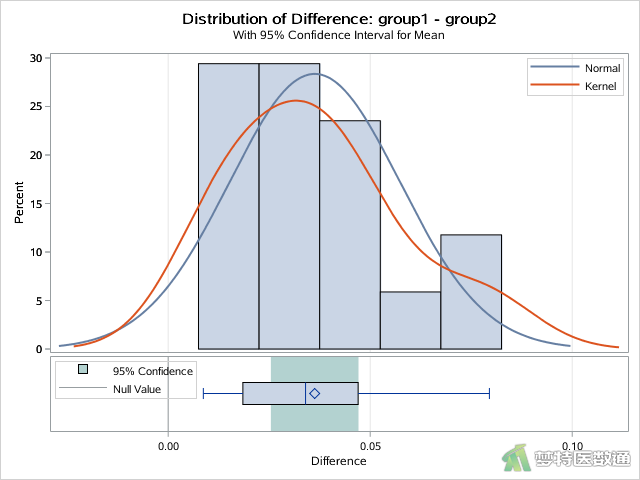
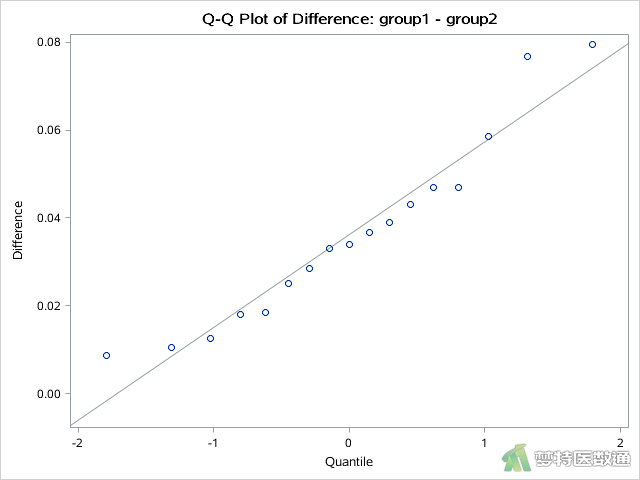
TTEST过程中默认输出直方图和Q-Q图可以快速检查两组差值是否满足t检验的正态性条件，如图8和图9所示。

(2)结果解读

图7的“Normality Test (Shapiro-Wilk) (夏皮罗-威尔克正态性)”表格结果显示两组差值服从正态分布(P=0.9332>0.1)；由图8的直方图可知，观察变量基本服从正态分布；此外图9的Q-Q图上散点基本围绕对角线分布，也提示数据呈正态分布。综上，本案例满足条件5。关于正态性检验的注意事项详见推文医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现。

(三)统计学描述及推断

1. 软件操作

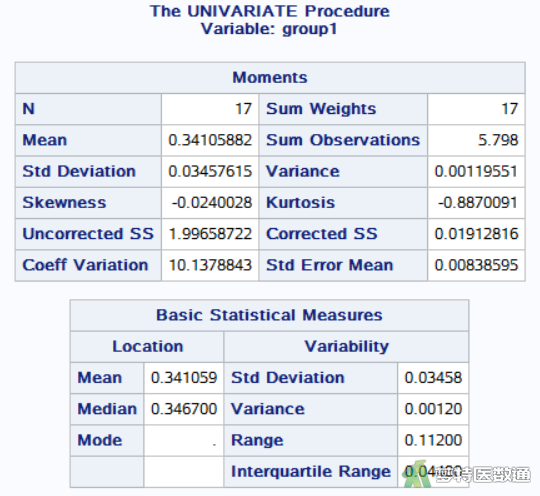
①运用先前步骤中UNIVARIATE过程得出两组统计学描述性分析结果：

proc univariate data= mydata.example plot;
var group1 group2;
run;

CORR过程同样给出描述性分析结果，但UNIVARIATE 过程默认给出较多小数位数，故此处选择UNIVARIATE 过程结果。

两组统计学描述性分析结果如图10和图11所示：

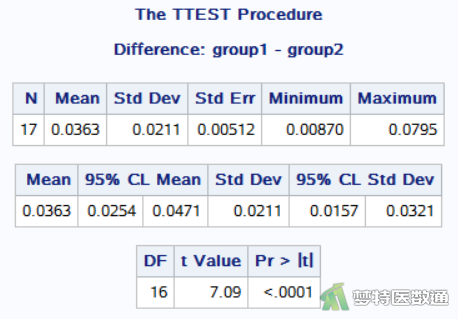
②运用先前步骤中TTEST过程得出配对t检验结果，如图12所示：

proc ttest data= mydata.example plots(shownull)=interval;
  paired group1*group2;
run;

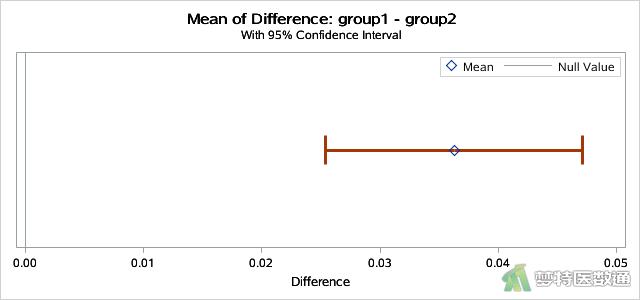
该步骤中还可以选择添加“plots(shownull)=interval”选项，可作置信区间图(图13)。

2. 结果解读

(1)统计学描述

图10和图11分别为A方法组 (group1)和B方法组 (group2)的“Descriptives (描述性分析)”表格，提供了研究案例的“N (样本量)”、“Mean (均数)”、“Std Dev (标准差)”、“Std Err (标准误)”、“Minimum (最小值)”和“Maximum(最大值)”等信息。由图可知，A方法组测量的生化指标(X)的含量为0.3411±0.0346，B方法组测量的生化指标(X)的含量为0.3048±0.0231。两组含量貌似存在差异，但还需要依据统计学检验的结果进行判断。

(2)统计学推断

图12的“Paired Samples T-Test (配对样本t检验)”表格中提供了统计学推断后的“Mean (均值)”及其“95% CL Mean (95%可信区间，95%CI)”、“Std Dev (标准差)”及其“95% CL Std Dev(95%CI)”。

可知A方法检测结果比B方法平均高0.0363，95%CI为0.0254~0.0471；差异有统计学意义(t=7.09，P<0.0001)。

(四)相关性分析

1. 软件操作

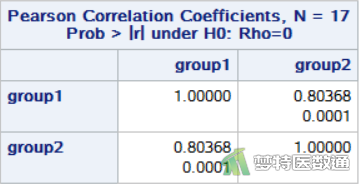
①运用CORR过程进行相关性检验，得到相关性检验结果如图14所示：

proc corr data= mydata.example;
  var group1 group2;
run;

②通过上一步TTEST过程得出数据的配对情况(如图15，图16所示)。

2. 结果解读

图14显示两组Pearson相关系数r = 0.80368，P = 0.0001，提示两组数据之间存在相关性；表明A、B两种方法之间的差异具有较好的稳定性。图15展示了数据的配对情况，每条细线左端为A组(group1)的值，右端为B组(group2)的值，红线为两组均值的比较，从图中我们可以轻易的观察到A、B两组配对观测之间的生化指标变化趋势，即下降趋势；图16的散点图也提示两组之间存在线性相关。

相关性的计算是为了验证配对数据的一致性，可以说明研究因素作用的稳定性或一致性，可能存在四种情况。①相关性检验与配对t检验的P值均<0.05，说明数据一致性较好，差异有统计学意义，而且差异的产生就是研究因素作用的结果。②相关性检验P>0.05，配对t检验的P<0.05，说明两组数据间存在差异，但对子间均数差异变化不一致，均数差异可能还受其他因素的影响。③相关性检验P<0.05，但配对t检验的P>0.05，说明数据变化有一致性，但均数差异不显著，即研究因素未发挥作用。④相关性检验与配对t检验的P值均>0.05，说明数据在两组间不具备一致性，且差异也无统计学意义。本案例为第①种情况。

四、结论

本研究采用配对样本t检验判断A、B两种方法检测肌肉组织中生化指标(X)的含量是否有差异。通过专业知识判断，数据不存在需要删除的异常值；通过绘制Q-Q图和Shapiro-Wilk检验，提示数据服从正态分布；通过绘制散点图和Pearson相关性分析，提示两组数据之间存在相关性。

结果显示，A、B方法检测肌肉组织中生化指标(X)的含量分别为0.3411±0.0346和0.3048±0.0231。A方法平均值比B方法高0.0363 (95%CI：0.0254~0.0471)，差异有统计学意义(t=7.09，P<0.0001)，两组Pearson相关系数 r = 0.80368，P = 0.0001；表明A、B两种方法之间的差异具有较好的稳定性。因此，本案例分析表明，使用A方法检测肌肉组织中生化指标(X)的含量通常会比B方法检测结果值要高。