独立样本t检验(Independent-Samples t-test)——SAS软件实现

关键词：SAS; t检验; 独立样本t检验; 成组t检验; 两样本均数比较; 近似t检验; 韦尔奇t检验; Welch近似t检验

一、案例介绍

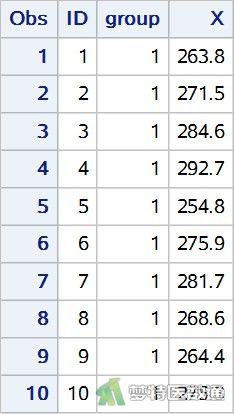
某医生研究某生化指标(X)对病毒性肝炎诊断的临床意义，测得20名正常人和19名病毒性肝炎患者某生化指标(X)含量(μg/dl)，问病毒性肝炎患者和正常人生化指标(X)含量是否存在差异？患者分组变量名记为group，分别赋值为1(正常人)和2(病毒性肝炎患者)。部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

研究者拟分析两组数据均值是否有差异，即判断正常人和病毒性肝炎患者生化指标(X)含量是否有差异。针对这种情况，可以使用独立样本t检验。但需要满足以下6个条件：

条件1：观察变量为连续变量。本研究中的生化指标含量为连续变量，该条件满足。

条件2： 观察变量之间相互独立。本研究中各研究对象的信息都是独立的，不存在互相干扰，该条件满足。

条件3：观察变量可分为2组。本研究中分为正常人和病毒性肝炎患者，该条件满足。

条件4：观察变量不存在显著的异常值，该条件需要通过软件分析后判断。

条件5：观察变量再各组内为正态(或近似正态)分布，该条件需要通过软件分析后判断。

条件6：两组观察变量的方差相等，该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一)导入数据

①利用LIBNAME语句建立SAS逻辑库关联，注意逻辑库名称要求，即最大长度8字符，必须以字母或下划线“_”开始，可以是字母、数字和下划线的任意组合。具体代码如下：

libname mydata "D:\mydata";

通过这一步骤，SAS能够识别引号中的物理位置，将逻辑库建立在该目录下，同时在以下过程中新建的SAS表格便可以永久储存在该位置，便于反复读取和使用。先运行该代码使其生效。

②使用PROC IMPORT语句导入数据集，指定原始数据集所在的物理位置“D:\mydata\独立样本T检验.csv”及数据格式为CSV，通过GETNAMES定义第1行为变量名以及DATAROW定义数据从第2行开始，最终数据集导入成名为mydata.ttest的SAS数据集。代码如下：

proc import out=mydata.ttest
	datafile = "D:\mydata\独立样本T检验.csv"
	dbms = csv replace;
	getnames = yes;
	datarow = 2;
run;

(二)适用条件判断

1. 条件4判断(异常值检测)

(1)软件操作

运用UNIVARIATE过程进行检验：

proc univariate data=mydata.ttest plot;
	class group;
	var X;
run;

其中“mydata.ttest”为自定义的数据表名称，“group”是两组患者分组变量，“X”为分析变量。选项PLOT产生了平行条状图，箱线图和正态概率图。CLASS过程以分组变量“group”分类，分别得到两组内分析变量的统计量等信息。

(2)结果解读

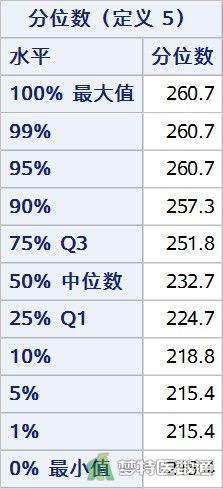
图2列出了组1 (group=1)观察变量的“0%最小值”、“100%最大值”和其他“百分位数”，依据专业可判断人体生化指标含量均可能存在254.80μg/dl和292.70μg/dl的情况。

图3列出了组2 (group=2)观察变量的“0%最小值”、“100%最大值”和其他“百分位数”，依据专业可判断人体生化指标含量均可能存在215.40μg/dl和260.70μg/dl的情况。综上，两组数据的最大值和最小值依据专业判断均非异常值。

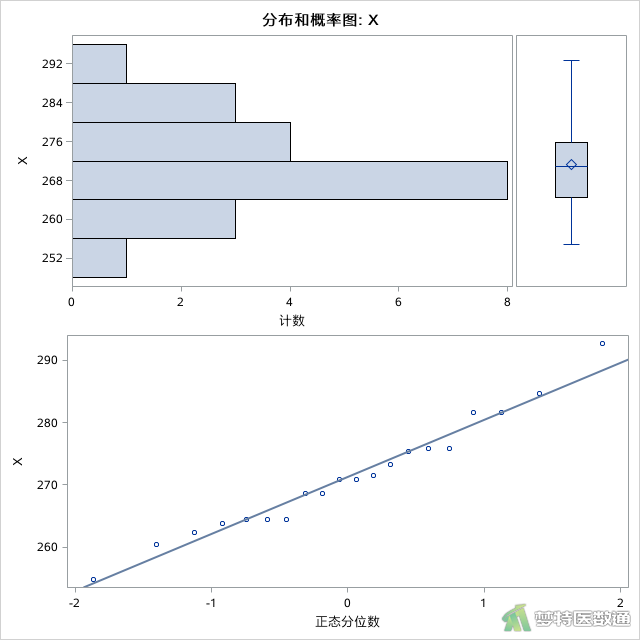
此外，图4和图5分别为组1 (group=1)和组2 (group=2)的平行条状图，箱线图和正态概率图，根据图形判断，也未发现任何异常值和极端值。综上，本案例未发现需要删除的异常值，满足条件4。

2. 条件5判断(正态性检验)

(1)软件操作

①运用前一步骤中UNIVARIATE 过程进行正态性检验：

proc univariate data=mydata.ttest normal;
	class group;
	var X;
run;

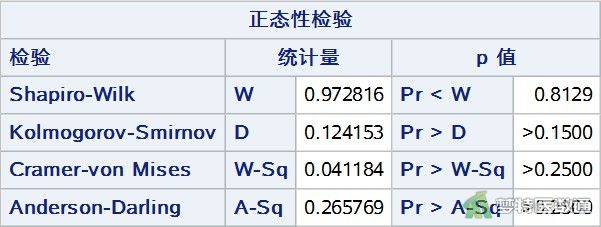
此处可延续上一步骤UNIVARIATE 过程，直接添加选项NORMAL，分别对两组进行正态性检验，得到组1 (group=1) (图6)和组2 (group=2) (图7)的“正态性检验”的结果。

②运用TTEST过程得出直方图和Q-Q图：

proc ttest data=mydata.ttest;
	class group;
	var X;
run;

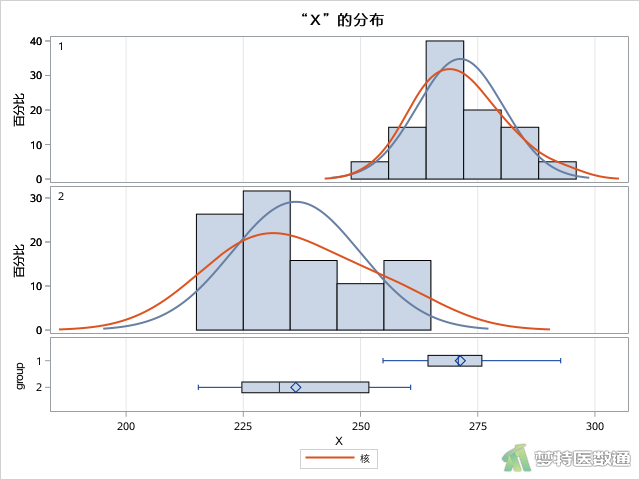
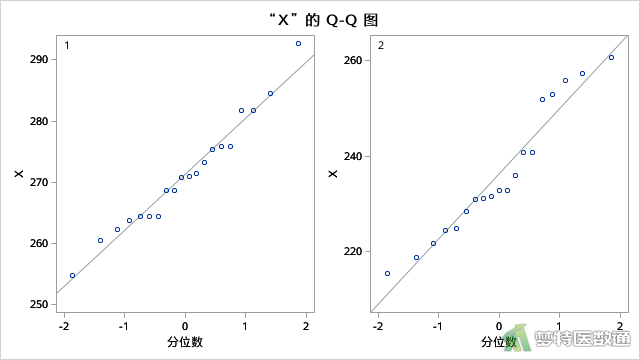
TTEST过程中默认输出两组数据的直方图(图8)和Q-Q图(图9)，可以快速检查数据是否满足t检验的正态性条件。

(2)结果解读

UNIVARIATE 过程所得图6和图7的正态性检验结果分别显示P=0.8129和0.1918，均>0.1，提示两组数据均服从正态分布；由图8的直方图可知，两组观察变量基本满足正态分布；图9的Q-Q图上两组散点基本围绕对角线分布，也提示两组数据呈正态分布。综上，本案例满足条件5。关于正态性检验的更多内容请阅读医学统计学核心概念及重要假设检验的软件实现(2/4) ——正态性假设检验的SPSS实现。

3. 条件6判断(方差齐性检验)

(1)软件操作

①前一步骤中TTEST过程能够直接得出方差齐性检验结果：

proc ttest data=mydata.ttest;
	class group;
	var X;
run;

此处程序默认得到的结果为F检验结果。

②另外，可以通过ANOVA过程得到方差齐性检验结果：

proc anova data = mydata.ttest;
	class group;
  	model x = group;
	means group / hovtest=levene(type=abs);
run;

此程序得到的结果是Levene检验结果。

(2)结果解读

图10列出了方差齐性检验的结果，可见F检验结果为：F=2.23，P= 0.0909<0.1；Levene检验结果为：F=3.88，P=0.0563<0.1，提示两组数据方差不齐，不满足条件6。

如果数据条件1-5都满足，仅不满足方差齐性，此时可使用近似t检验的结果，即查看Satterthwaite方法的t值与P值。

(三)统计描述及推断

1. 软件操作

运用先前步骤中TTEST过程，得出方差齐性检验结果：

proc ttest data=mydata.ttest plots(shownull)=interval;
	class group;
	var x;
run;

该步骤中还可以选择添加“plots(shownull)=interval”选项，可作置信区间图(图11)。

2. 结果解读

(1)统计学描述

TTEST过程提供了研究案例的“N (样本量)”、“Mean (均值)”、“Std Dev (标准差)”、“Std Err (标准误差)”、“Minimum (最小值)”和“Maximum(最大值)”(图12)。正常人群的生化指标X含量为271.3±9.1683μg/dl，肝炎患者的含量为236.2±13.6952μg/dl。两组的X含量貌似存在差异，但还需要依据统计学检验的结果进行判断。

(2)统计学推断

图13的表格中提供了两组及两组差值统计学推断的“Mean (均值)”及其“95% CI Mean (95%可信区间，95%CI)”、“Std Dev(标准差)”及其“95% CI Std Dev(95%CI)”。

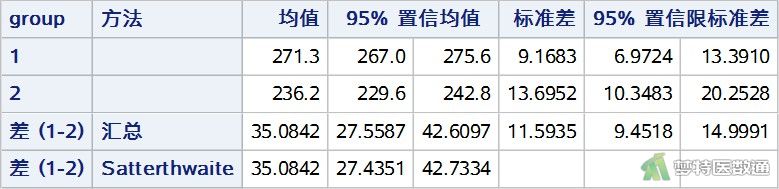
可知肝炎患者的X含量平均值比正常人群低35.0842μg/dl，95%CI为27.4351~ 42.7334。

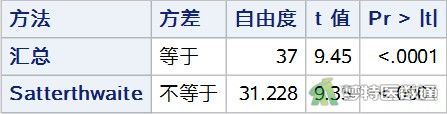
图14给出t检验和校正t检验两种方法的“t Value (t值)”、“DF(自由度)”和P值。数据已满足条件1-5，仅不满足方差齐性，此时可使用近似t检验(Satterthwaite检验)的结果，差异有统计学意义(t’=9.35，P<0.0001)。

四、结论

本研究采用独立样本t检验判断病毒性肝炎患者和正常人某生化指标X含量是否存在差异。研究数据不存在异常值，各组数据接近正态分布，组间方差不齐。结果显示，正常人群和肝炎患者的生化指标含量分别为271.3±9.1683μg/dl 和236.2±13.6952μg/dl，肝炎患者的生化指标含量平均值比正常人群低35.0842μg /dl (95%CI：27.4351~42.7334)，差异有统计学意义(t’=9.35，P<0.0001)。因此，该生化指标含量对病毒性肝炎的临床诊断具有价值。