独立样本t检验又称成组t检验(two-sample/group t-test)或两独立样本t检验(two independent-sample t-test),医学研究中常用于完全随机设计两样本均数的比较,即将受试对象完全随机分配到两个不同处理组,研究者关心的是两样本均数所代表的两总体均数是否不等。此外,在观察性研究中,独立从两个总体中进行完全随机抽样,获得的两样本均数的比较,也可采用独立样本t检验。
关键词:t检验; 独立样本t检验; 成组t检验; 两样本均数比较; 近似t检验; 韦尔奇t检验; Welch近似t检验
一、适用条件
独立样本t检验,需要满足六个条件:
条件1:观察变量为连续变量。
条件2:观察变量相互独立。
条件3:观察变量分为2组。
条件4:观察变量不存在显著的异常值。
条件5:各组观察变量为正态(或近似正态)分布。
条件6:两组观察变量的方差相等。
二、统计量计算
当两样本均来自正态总体,但样本含量较小,如n1≤60或/和n2≤60时,要根据两总体方差是否相等而采用不同检验方法。
(一) 总体方差相等的t检验
当两总体方差相等,即\( \sigma_{1}^{2}=\sigma_{2}^{2} \)时,可将两样本方差合并,求两者的共同方差——合并方差 \( S_{c}^{2} \) 。
两样本t检验的检验统计量可按照单样本t检验(One Sample t-test)统计量计算公式进行计算,在 \( H_{0}: \mu_{1}=\mu_{2} \) ,即 \( \mu=\mu_{1}-\mu_{2}=\mu_{0}=0 \) 条件下构造。其检验统计量为:
\( t=\frac{\left(\bar{X}_{1}-\bar{X}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{s_{\bar{X}_{1}-\bar{X}_{2}}}=\frac{\bar{X}_{1}-\bar{X}_{2}}{s_{\bar{X}_{1}-\bar{X}_{2}}} \) , \( \quad v=n_{1}+n_{2}-2 \)
即 \(t=\frac{\bar{X}_{1}-\bar{X}_{2}}{\sqrt{s_{c}^{2}\left(\frac{1}{n_{1}}+\frac{1}{n_{2}}\right)}}\)
\( =\frac{\bar{X}_{1}-\bar{X}_{2}}{\sqrt{\frac{\sum X_{1}^{2}-\left(\sum X_{1}\right)^{2} / n_{1}+\sum X_{2}^{2}-\left(\sum X_{2}\right)^{2} / n_{2}}{n_{1}+n_{2}-2}\left(\frac{1}{n_{1}}+\frac{1}{n_{2}}\right)}} \)\( =\frac{\bar{x}_{1}-\bar{X}_{2}}{\sqrt{\frac{\left(n_{1}-1\right) S_{1}^{2}+\left(n_{2}-1\right) S_{2}^{2}}{n_{1}+n_{2}-2}\left(\frac{1}{n_{1}}+\frac{1}{n_{2}}\right)}} \) ,\( \quad v=n_{1}+n_{2}-2 \)
(二) 总体方差不等的近似t检验
进行两小样本均数比较,若总体服从正态分布,但两总体方差不等,即 \( \sigma_{1}^{2} \neq \sigma_{2}^{2} \) 时,可采用数据变换(如两样本几何均数的t检验,就是将原始数据取对数后进行t检验)或下述近似t检验——t′检验或秩转换的非参数检验。
近似t检验有以下三种方法可供选择:Cochran & Cox法、Satterthwaite法和Welch法。
1. Cochran & Cox近似t检验
Cochran& Cox法(1950)的检验统计量为t′,按下方公式计算。因t′分布较复杂,故常利用t计算其近似临界值 \( t_{\alpha}^{\prime} \) 。
\( t^{\prime}=\frac{\bar{X}_{1}-\bar{X}_{2}}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}, \quad v_{1}=\mathrm{n}_{1}-1 \) , \( \quad v_{2}=\mathrm{n}_{2}-1 \) ,
\( t_{\alpha}^{\prime}=\frac{S_{X_{1}}^{2} \cdot t_{\alpha, v_{1}}+S_{\bar{X}_{2}}^{2} \cdot t_{\alpha, v_{2}}}{S_{\bar{X}_{1}}^{2}+S_{\bar{X}_{2}}^{2}} \)t′值与P值的关系同t值与P值的关系。注意:①当 \( n_{1}=n_{2}=n \) 时, \( v_{1}=v_{2}=v \) , \( t^{\prime}=t \) , \( \quad t_{\alpha}^{\prime}=t_{\alpha, v} \) ,v=n-1(不是2n-2);②用双侧概率时, \( t_{\alpha}^{\prime}=t_{\alpha / 2}^{\prime} \) , \( t_{\alpha, v_{2}} \) 取 \( t_{\alpha / 2, v_{1}} \) 和 \( t_{\alpha / 2, v_{2}} \) 。
2. Satterthwaite近似t检验
Cochran & Cox法是对临界值校正,而Satterthwaite法(1946)则是对自由度校正。即用上述公式中的t′代替t,自由度校正按以下公式计算。最终结果根据(t界值表)进行判定。
\(t=t^{\prime}, \quad v=\frac{\left(s \frac{2}{X_{1}}+S_{\bar{X}_{2}}^{2}\right)^{2}}{\frac{s_{\bar{X}_{1}}^{4}}{n_{1}-1}+\frac{s_{\bar{X}_{2}}^{4}}{n_{2}-1}}=\frac{\left(\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}\right)^{2}}{\frac{\left(\frac{s_{1}^{2}}{n_{1}}\right)^{2}}{n_{1}-1}+\frac{\left(\frac{s_{2}^{2}}{n_{2}}\right)^{2}}{n_{2}-1}}\)3. Welch近似t检验
Welch法(1947)也是对自由度进行校正。其校正按以下公式计算得
\( t=t^{\prime}, \quad v=\frac{\left(s_{X_{1}}^{2}+S_{X_{2}}^{2}\right)^{2}}{\frac{s_{X_{1}}^{4}}{n_{1}+1}+\frac{s_{X_{2}}}{n_{2}+1}}-2=\frac{\left(\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}\right)^{2}}{\frac{\left(\frac{s_{1}^{2}}{n_{1}}\right)^{2}}{n_{1}+1}+\frac{\left(\frac{s_{2}^{2}}{n_{2}}\right)^{2}}{n_{2}+1}}-2 \)三、案例数据
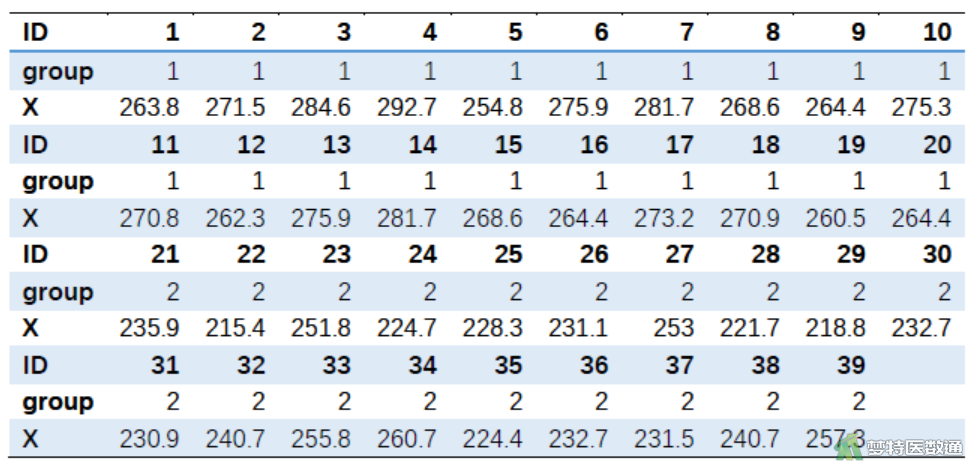
某医生研究某生化指标(X)对病毒性肝炎诊断的临床意义,测得20名正常人和19名病毒性肝炎患者生化指标(X)含量(μg/dl),问病毒性肝炎患者和正常人生化指标(X)含量是否存在差异?数据见图1。
四、假设检验
(一) 方差齐性检验
此处使用Levene检验进行方差齐性检验,由于该检验的计算量巨大,使用jamovi软件完成计算过程。

从图2“Homogeneity of Variances Test (Levene's) (Levene方差齐性检验)”结果可知,F=3.883,P=0.056<0.1,提示两组数据方差不齐,故采用近似t检验。
(二) Cochran & Cox近似t检验
1. 建立检验假设,确定检验水准
H0:μ1= μ2,即病毒性肝炎患者和正常人生化指标(X)含量均数相等
H1:μ1 ≠ μ2,即病毒性肝炎患者和正常人生化指标(X)含量均数不等
2. 计算检验统计量
\( \bar{X}_{1}=271.300,\bar{X}_{2}=236.216,{S}_{1}=9.168,{S}_{2}=13.695 \) ,按Cochran & Cox近似t检验统计量计算公式得:
\( t'=\frac{271.300-236.216}{\sqrt{\frac{9.168^2}{20}+\frac{13.695^2}{19}}},\quad v_1=20-1=19,\quad v_2=19-1=18 \)查(t界值表),t0.05/2,19=2.093,t0.05/2,18=2.101,计算 \( t^{\prime} \) 得:
\(t'_{0.05/2}=\frac{(\frac{9.168}{\sqrt{20}})^2\times2.093+(\frac{13.695}{\sqrt{19}})^2\times2.101}{(\frac{9.168}{\sqrt{20}})^2+(\frac{13.695}{\sqrt{19}})^2}=2.098611\)3. 确定P值,作出推断结论
由|t′|=9.352>2.098611得P<0.05。按a = 0.05水准,拒绝H0,接受H1,差异有统计学意义。可以认为病毒性肝炎患者和正常人生化指标(X)含量存在差异。
(三) Satterthwaite近似t检验
1. 建立检验假设,确定检验水准
H0:μ1= μ2,即病毒性肝炎患者和正常人生化指标(X)含量均数相等
H1:μ1 ≠ μ2,即病毒性肝炎患者和正常人生化指标(X)含量均数不等
α = 0.05
2. 计算检验统计量
\( \bar{X}_{1}=271.300,\bar{X}_{2}=236.216,{S}_{1}=9.168,{S}_{2}=13.695 \) ,按Cochran & Cox近似t检验统计量计算公式得:
\( t'=\frac{271.300-236.216}{\sqrt{\frac{9.168^2}{20}+\frac{13.695^2}{19}}},\quad v_1=20-1=19,\quad v_2=19-1=18 \)根据Satterthwaite法自由度校正公式计算可得:
\(v=\frac{(\frac{9.168^2}{20}+\frac{13.695^2}{19})^2}{\frac{(\frac{9.168^2}{20})^2}{20-1}+\frac{(\frac{13.695^2}{19})^2}{19-1}}=31.227169 \)3. 确定P值,作出推断结论
以V=32查(t界值表)得 \(t'_{0.001 / 2, 32}=3.622 \) ,即\( |t'|=9.352>t'_{0.001 / 2, 32}=3.622 \) ,得P<0.001。按α=0.05水准,拒绝H0,接受H1,差异具有统计学意义。可以认为病毒性肝炎患者和正常人生化指标(X)含量存在差异。结论与Cochran & Cox近似t检验一致。
(四) Welch近似t检验
1. 建立检验假设,确定检验水准
H0:μ1= μ2,即病毒性肝炎患者和正常人生化指标(X)含量均数相等
H1:μ1 ≠ μ2,即病毒性肝炎患者和正常人生化指标(X)含量均数不等
α = 0.05
2. 计算检验统计量
\( \bar{X}_{1}=271.300,\bar{X}_{2}=236.216,{S}_{1}=9。168,{S}_{2}=13.695 \) ,按Cochran & Cox近似t检验统计量计算公式得:
\( t'=\frac{271.300-236.216}{\sqrt{\frac{9.168^2}{20}+\frac{13.695^2}{19}}},\quad v_1=20-1=19,\quad v_2=19-1=18 \)根据Welch法自由度校正公式计算可得:
\(v=\frac{(\frac{9.168^2}{20}+\frac{13.695^2}{19})^2}{\frac{(\frac{9.168^2}{20})^2}{20+1}+\frac{(\frac{13.695^2}{19})^2}{19+1}}-2=32.66997\)3. 确定P值,作出推断结论
以V=33查(t界值表)得 \( t'_{0.001 / 2, 33}=3.611 \) ,即 \( |t'|=9.352>t'_{0.001 / 2, 33}=3.611 \) ,得P<0.001。按α=0.05水准,拒绝H0,接受H1,差异具有统计学意义。可以认为病毒性肝炎患者和正常人生化指标(X)含量存在差异。结论与Cochran & Cox近似t检验和Satterthwaite近似t检验一致。