在前面文章中介绍了两因素重复测量方差分析(Two-way Repeated-Measures ANOVA)的假设检验理论,本篇文章将实例演示在Stata软件中实现两因素重复测量方差分析——不存在交互作用时的操作步骤。
关键词:Stata; 重复测量; 重复测量资料; 重复测量方差分析; 两因素重复测量方差分析; 球形检验; 交互作用; 主效应; 单独效应
一、案例介绍
研究A、B两种饲料对家兔的增重效果,选择20只家兔,随机分成两组,第一组用饲料A饲养,第二组用饲料B饲养,并于试验开始后第一个月(time1)、第二个月(time2)、第三个月(time3)分别测量2组家兔体重,试比较A、B两种饲料对家兔的增重效果有无差别?部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析
本案例的分析目的是比较A、B两种饲料对家兔的增重效果有无差别。由于3个时间点的数据属于重复测量数据,且有两个组别,可以使用两因素(时间因素time和分组因素group)重复测量方差分析。但需要满足以下6个条件:
条件1:观察变量唯一,且为连续变量。本研究中观察变量只有体重,且为连续变量,该条件满足。
条件2:有两个分析因素。本研究有时间因素time和分组因素group两个因素,该条件满足。
条件3:观察变量为重复测量数据,即不满足独立性。本研究中两个组别在3个时间点时测量的体重均是针对同一批样本,因此不满足独立性,该条件满足。
条件4:观察变量不存在显著的异常值,该条件需要通过软件分析后判断。
条件5:各组、各水平(时间点)观察变量为正态(或近似正态)分布,该条件需要通过软件分析后判断。
条件6:相互比较的各处理水平(组别)的总体方差齐,该条件需要通过软件分析后判断。
三、软件操作及结果解读
(一) 适用条件判断
1. 条件4判断(异常值判断)
(1) 软件操作
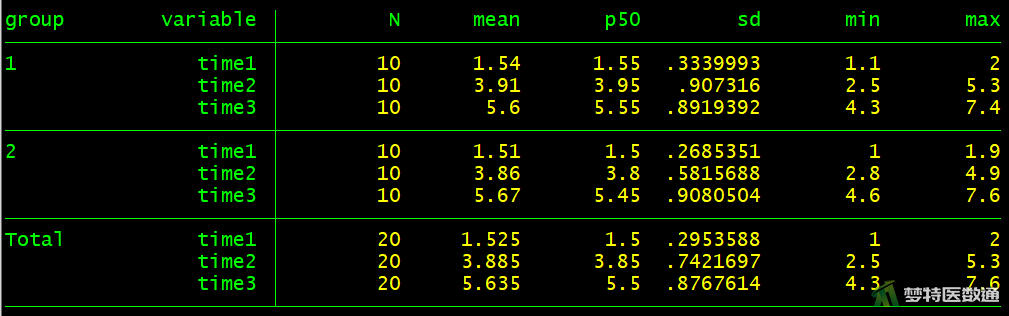
①计算描述性统计量,结果如图2所示。
tabstat time1 time2 time3,by(group) stat(count mean median sd min max) col(stat) long
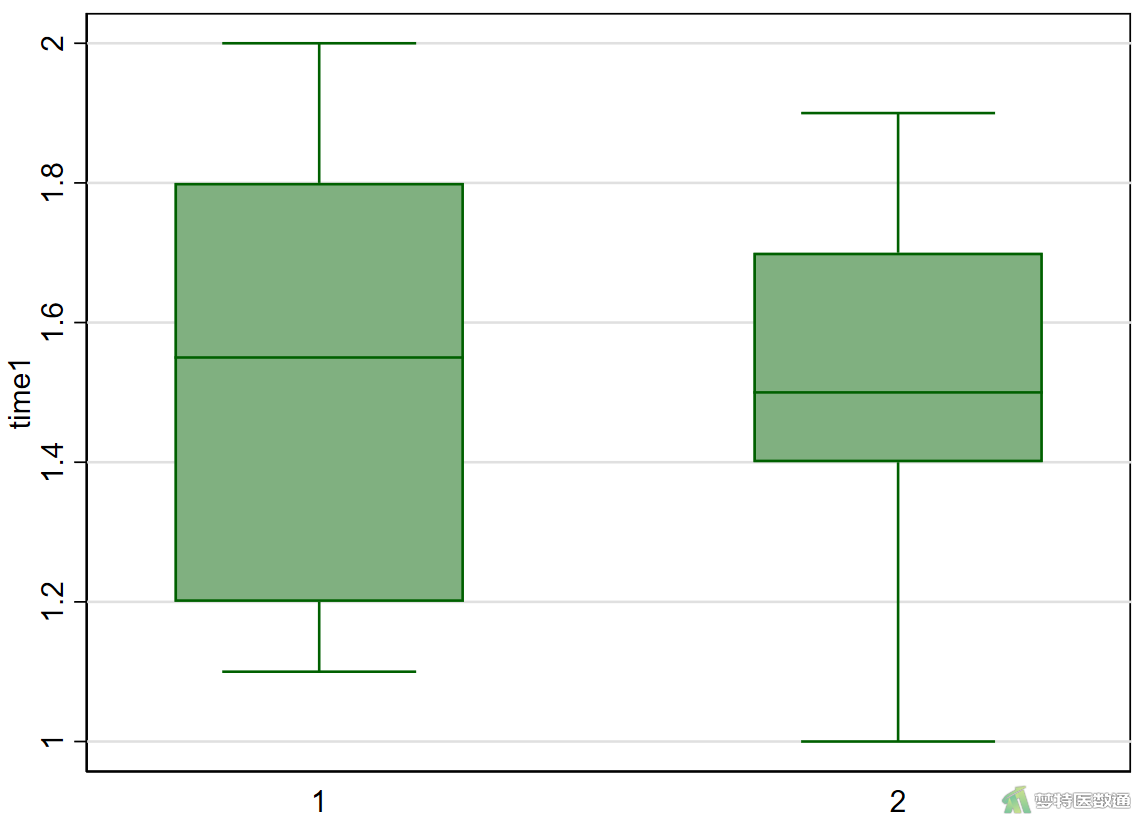
②绘制箱线图检查是否存在异常值,结果如图3-1—图3-3所示。
graph box time1, over(group) graph box time2, over(group) graph box time3, over(group)

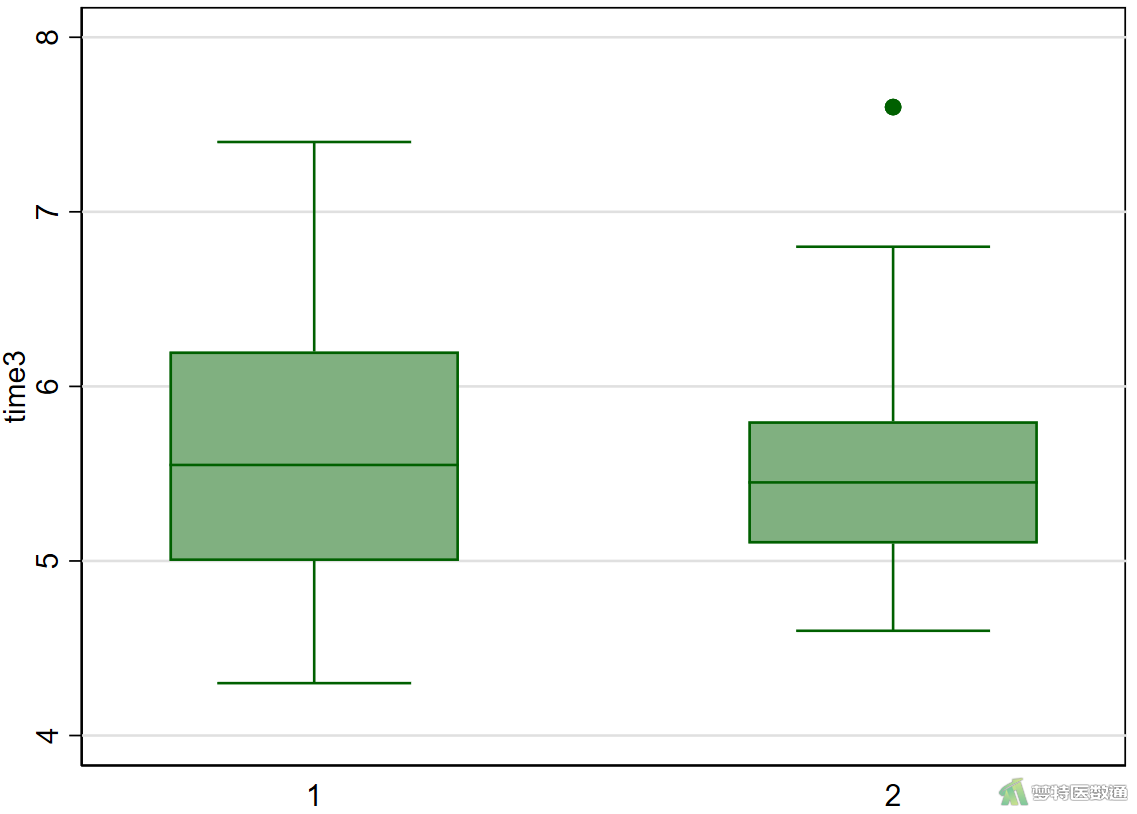
(2) 结果解读
图2的结果中列出了各组观察变量的最小值和最大值,依据专业尚不能认为存在异常值的情况;此外,图3-1的箱线图也未提示任何异常值,图3-2和图3-3中分别存在一个离群值,但根据专业尚不能判定为异常值。综上,本案例未发现需要处理的异常值,满足条件4。
2. 条件5判断(正态性检验)
(1) 软件操作
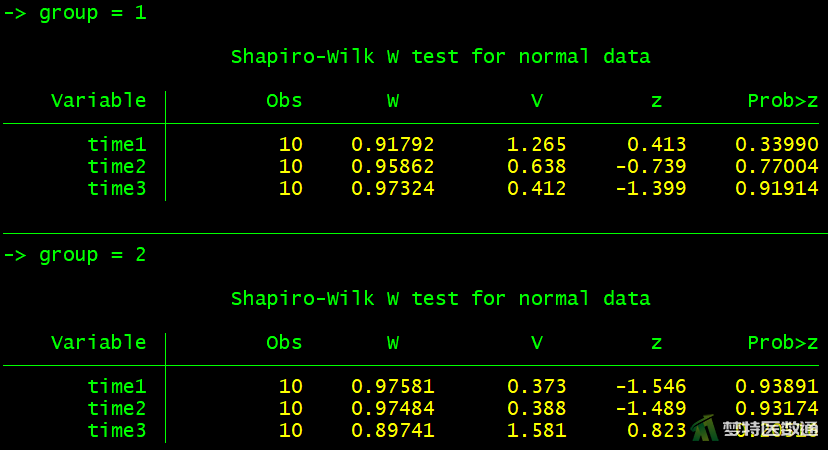
两因素重复测量方差分析时,需要分别考察每一组的正态性情况,结果如图4所示。
bysort group: swilk time1 time2 time3
(2) 结果解读
图4的正态性检验结果显示A组(group=1)三个时间点P=0.340、0.770、0.919,B组(group=2)三个时间点P=0.939、0.932、0.205,均>0.1,提示各组数据均服从正态分布。此外,本案例也可以绘制Q-Q图,结果也提示各组数据均服从正态分布(请读者自行操作)。综上,本案例满足条件5。关于正态性检验的注意事项详见文章(医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现)。
3. 条件6判断(方差齐性检验)
(1) 软件操作
robvar time1, by(group) robvar time2, by(group) robvar time3, by(group)
结果如图5-1—图5-3所示。
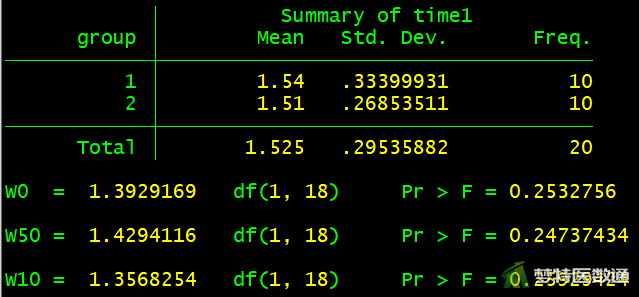
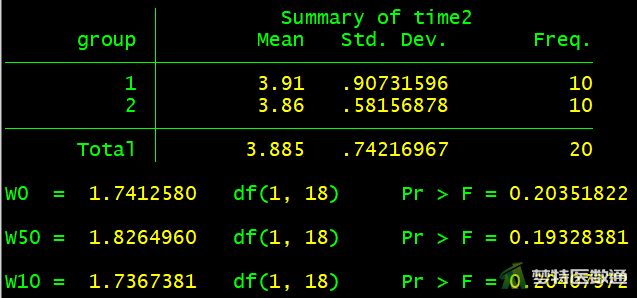
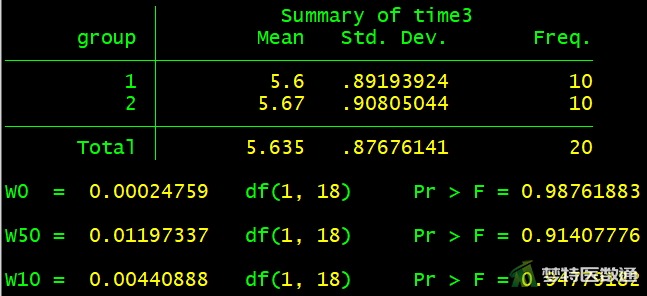
(2) 结果解读
图5-1—图5-3的方差齐性检验结果显示,time1、time2、time3时,两组之间的方差齐性检验结果分别为F=1.393、P=0.253,F=1.741、P=0.204,F=2.476e-4、P=0.988;提示每个时间点的两组之间都满足方差齐性。本案例满足条件6。关于方差齐性检验的更多内容请阅读(医学统计学核心概念及重要假设检验的软件实现(4/4)——方差齐性检验及SPSS实现)。
(二) 球形假设检验
1. 软件操作
安装“mauchly包”后可直接输入以下命令,结果如图6所示。“mauchly包”的安装详见“单因素重复测量方差分析(One-Way Repeated Measures ANOVA)——Stata软件实现”。
mauchly time1 time2 time3

2. 结果解读
由图6的结果可知,W=0.884,P=0.330,表示满足球形假设。可见,本案例满足条件7,无需校正。
(三) 统计描述
1. 软件操作
①生成一个序号变量“id”,部分数据如图7所示。
gen id=_n
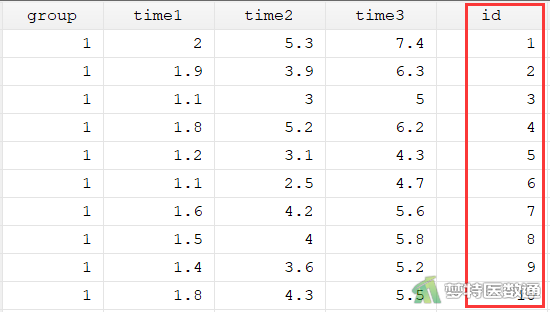
②变换数据显示格式,从“wide format”变换为“long format”,变换后部分数据如图8所示。
reshape long time, i(id) j(shike)
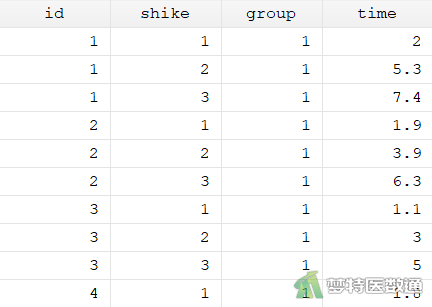
③数据变换格式后,变量shike对应的是时间,变量time对应的是体重,为了和前面分析保持一致,修改变量名称。
rename time y rename shike time
修改变量名称后,变量time表示时间,变量y表示体重,部分数据如图9所示。
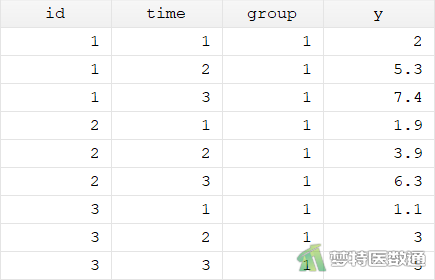
④进行方差分析和边际均值分析,结果如图10—图12所示。
anova y group / id|group time group#time, repeated(time) margins time, over(group) plot
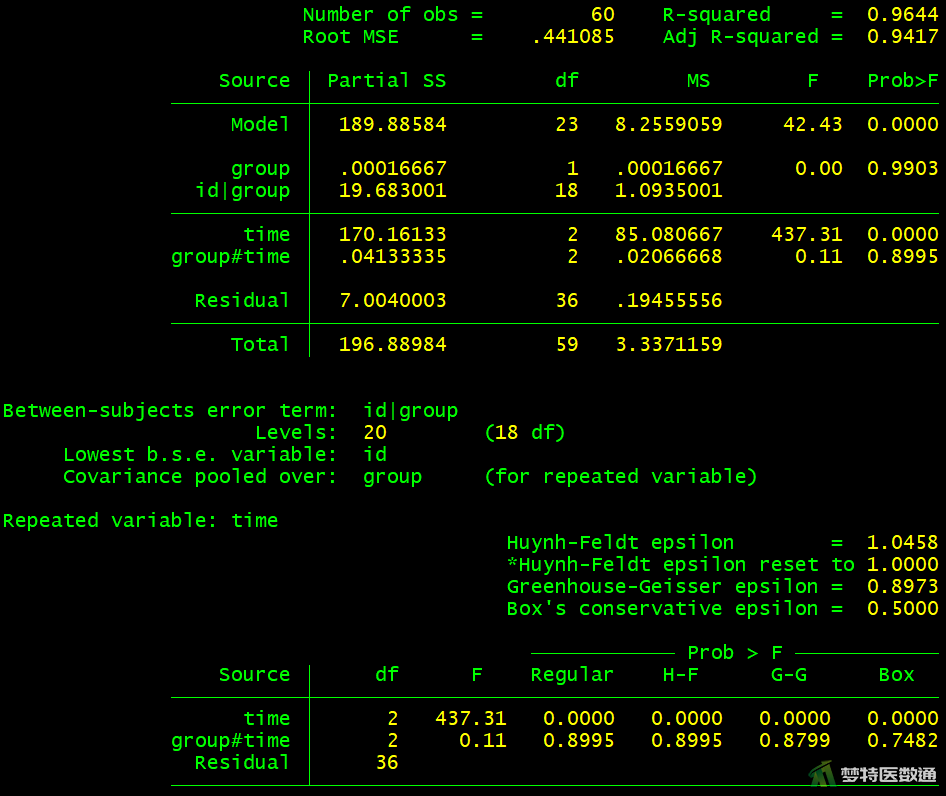
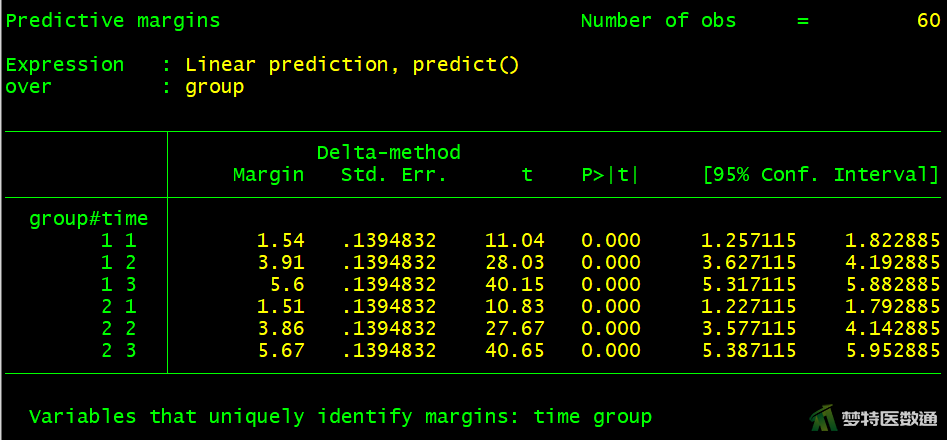
2. 结果解读
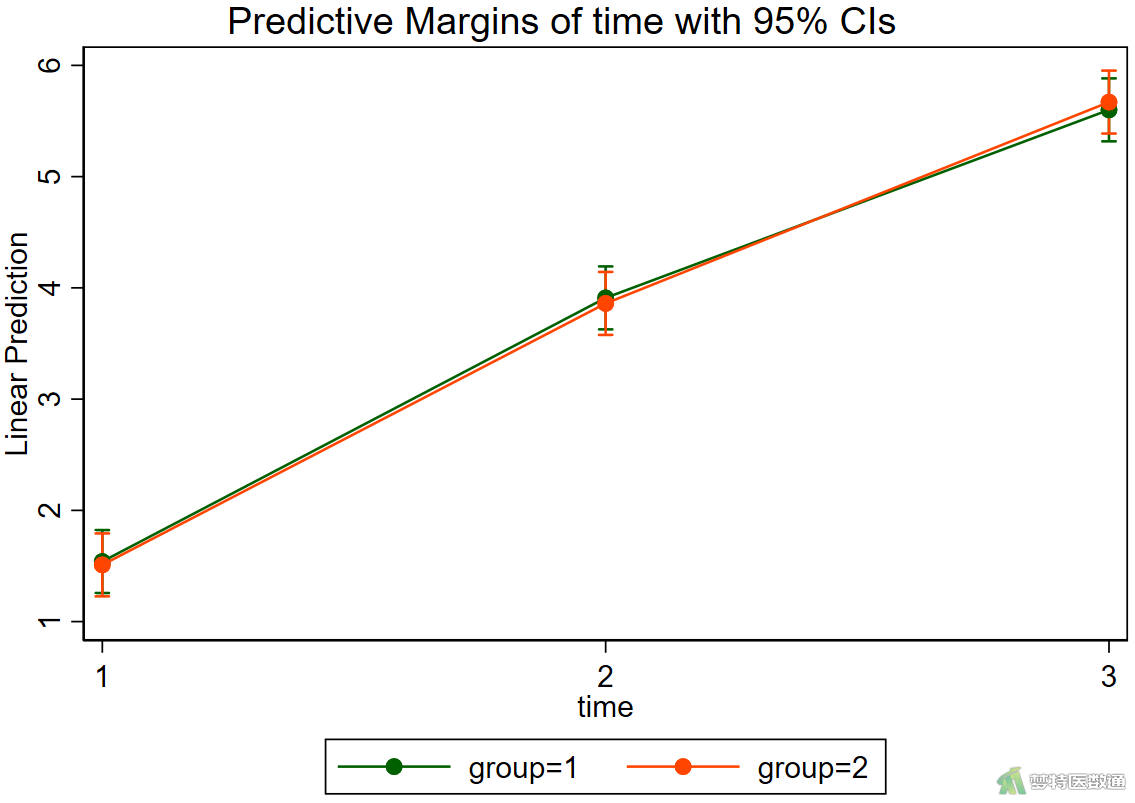
图10列出了两因素重复测量方差分析的结果。图11的结果中提供了两组三个时间点的边际均值相关统计量。图12的估算边际均值图绘制了两组三个时间点体重的变化情况,可见两组的体重均有增加,并且增加的幅度基本保持一致。
(四) 交互作用判断
由于本案例有两个因素(一个为时间因素time,另一个为分组因素group),因此需要首先判断两个因素之间是否存在交互作用。如果交互作用有统计学意义,则需要分析单独效应。
图10的方差分析结果中列出了两个表,上方的表格显示了重复测量的两因素方差分析结果,下方的表格结果显示了在不满足球形假设时,用Hunyh-Feldt 、Greenhouse-Geisser、Box's conservative三种方法校正的结果。根据之前的分析可知,本案例满足球形检验,不需要校正,因此只需参考上方的表格结果即可。可知,group与time之间的交互作用结果为Fgroup#time=0.11,P=0.900,提示group与time之间的交互作用无统计学意义。因此,本案例可直接以主效应分析结果进行判断,如果交互作用有统计学意义,则需要分析单独效应。
(五) 时间效应分析
根据图10中结果可知,Ftime=437.31,P<0.001,认为体重变化的时间趋势具有统计学意义。
(六) 组间效应分析
根据图10中结果可知,Fgroup=0.00,P=0.990,表示两种饲料对家兔的增重效果差异无统计学意义。
(七) 事后检验(两两比较)
上面分析得出了“体重变化的时间趋势具有统计学意义”的结论,即不同时间点之间体重差异有统计学意义,但到底是哪些时间点之间存在差异尚不清楚,因此需要进行事后检验,开展两两比较。
1. 软件操作
pwcompare time, effects pwcompare time, effects bonferroni
结果如图13-1和图13-2所示。
2. 结果解读
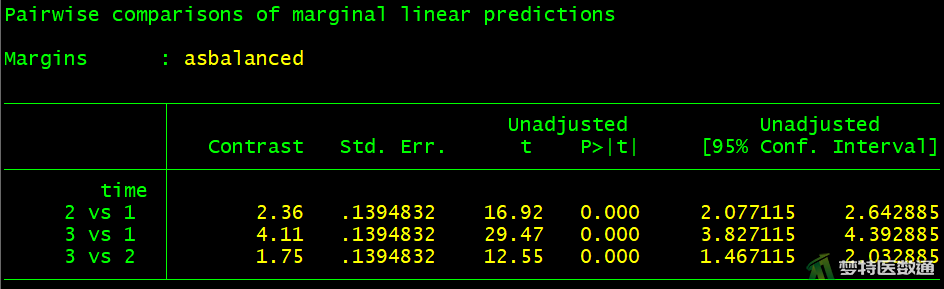
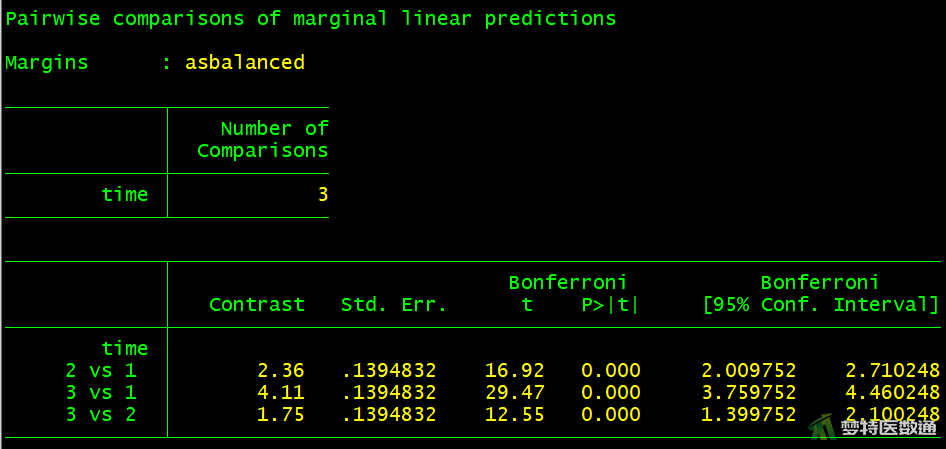
图13-1和图13-2分别显示了未校正和使用Bonferroni校正法进行两两比较的结果。可知,随着时间的延长,各时刻与时刻1相比,均值差逐渐增大。时刻2比时刻1时均值增加了2.360 kg,至时刻3时增加了4.11 kg,时刻2到时刻3时增加了1.75 kg,差异均有统计学意义(P<0.001)。
四、结论
本研究采用两因素重复测量方差分析比较A、B两种饲料对家兔的增重效果有无差别。通过专业知识判断,数据不存在异常值;通过Shapiro-Wilk检验,提示各组数据服从正态分布;通过Levene’s检验,提示每个时间点的两组之间都满足方差齐性;球形检验提示,满足球形假设(W=0.884,P=0.330);组别与时间无交互作用(Fgroup#time=0.11,P=0.900),故进行主效应分析。
A、B两组在试验开始后第1个月、第2个月和第3个月时的体重分别为1.540±0.334、3.910±0.907、5.600±0.892kg和1.510±0.269、3.860±0.582、5.670±0.908kg。两因素重复测量方差分析结果显示,在试验开始后第1个月、第2个月和第3个月2组家兔的体重均呈上升趋势(Ftime =437.31,P<0.001),但两种饲料对家兔的增重效果差异无统计学意义(Fgroup =0.00,P=0.990)。进一步采用Bonferroni校正法进行两两比较可知,随着时间的延长,第2个月和第3个月与第1个月时相比,体重增加均有统计学意义(P<0.001)。综上可知,两种饲料对家兔的增重效果差异无统计学意义。