在前面文章中介绍了随机区组设计方差分析(Randomized Block Design ANOVA)——Stata软件实现(链接),本文进一步介绍仅研究主效应的实验设计中的两阶段交叉设计方差分析(Two-stage cross-over design ANOVA)在Stata软件中的实现步骤。
关键词:Stata; 交叉设计; 两阶段交叉设计; 方差分析; 仅研究主效应的实验设计
在医学研究中,若将A、B两种处理先后施加于同一批实验对象,随机地使一半实验对象先接受A后接受B,另一半对象先接受B后接受A,这种设计称为两阶段交叉设计(Crossover Design)。应用方差分析的变异分解思想,此种设计的总变异可以分解为处理效应、阶段效应、受试者间的个体差异及随机误差共4项。需要注意的是,该设计有一个限制条件,即前一个阶段的处理效应不能持续到下一个阶段。因此在实际研究设计时,往往在两阶段间设置一个洗脱阶段。
一、案例介绍
假设有一项两阶段交叉试验,分别使用A、B两种药物治疗同一批共10例患者,检测某指标的血浆浓度。对10例患者随机编号,第一阶段样本编号(testid)为奇数的5例患者用A药物治疗,样本编号(testid)为偶数的5例患者用B药物治疗。第二阶段对调治疗药物,即样本编号(testid)为奇数的患者用B药物,样本编号(testid)为偶数的药物用A药物。试对该两阶段交叉实验结果进行方差分析,评估药物效果。数据见图1。本案例数据可从“附件下载”处下载。
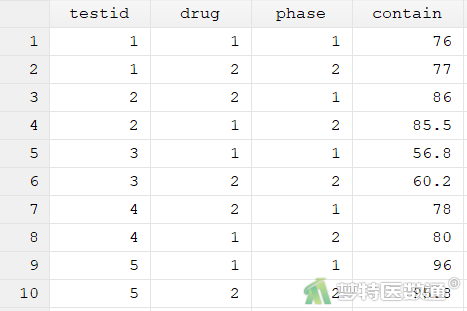
二、问题分析
在两阶段交叉数据分析,可以按照三因素方差分析思路进行数据处理。但需要满足6个条件:
条件1:观察变量唯一,且为连续变量。本研究中观察变量只有某指标的血浆浓度,且为连续变量,该条件满足。
条件2:有3个因素,且都为分类变量。本研究中有处理效应(A、B两种药物)、阶段效应及受试者间的个体差异,都为分类变量,该条件满足。
条件3:观测值相互独立。本研究中各研究对象的观测值都是独立的,不存在互相干扰的情况,该条件满足。
条件4:相互比较的各处理水平(组别)的总体方差相等,即方差齐同,可采用方差齐性检验。该条件需要通过软件分析后判断。
条件5:各组、各水平观测值为正态(或近似正态)分布。该条件需要通过软件分析后判断。
条件6:观察变量不存在显著的异常值。该条件需要通过软件分析后判断。
三、软件操作及结果解读
(一) 导入数据
(二) 适用条件判断
条件4~6需要通过模型残差进行判断,因此先生成模型残差。
1. 生成模型残差(图2)
anova contain testid drug phase predict e, res
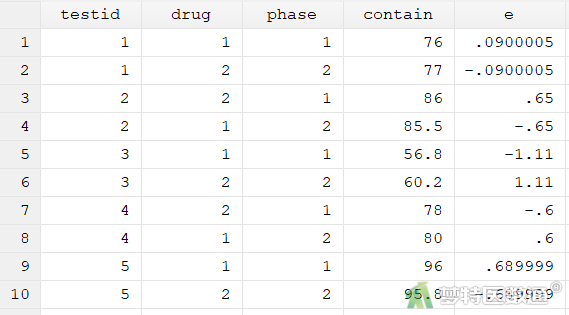
2. 条件4判断(方差齐性检验)
(1) 软件操作
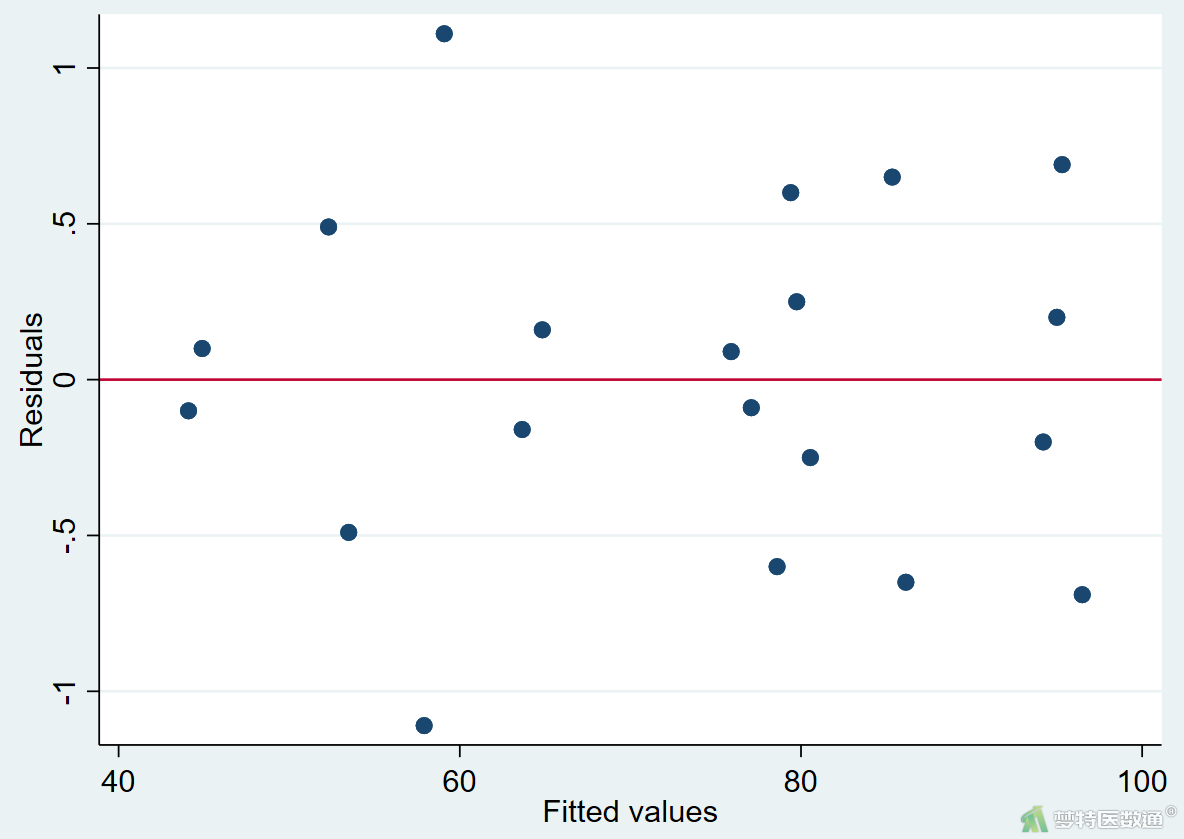
绘制残差图,语句如下,结果见图3。
rvfplot, yline(0)
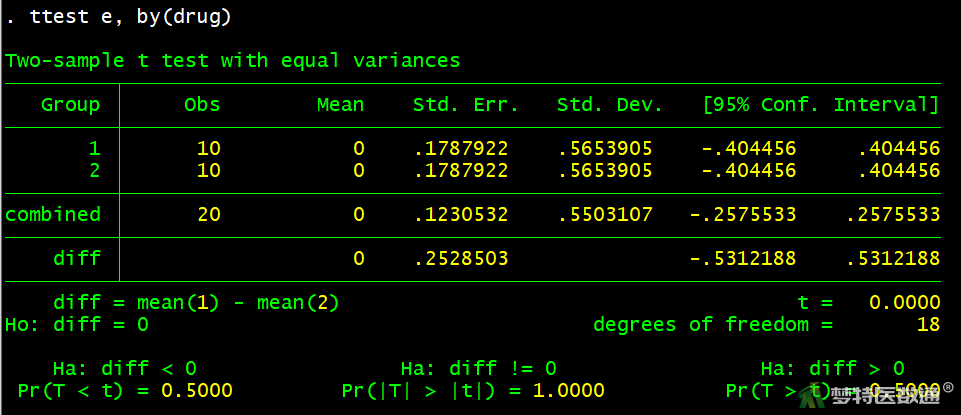
使用统计学推断检验方差齐性,语句如下,结果见图4。
ttest e, by(drug)
(2) 结果解读
由残差图(图3)可见,残差均匀地分布在其均值的上下两侧,提示观察变量的残差满足方差齐性。残差的方差齐性检验结果(图4)显示,P=1.000>0.1,提示相互比较的各处理水平的总体方差相等。本案例满足条件4。
3. 条件5判断(正态性检验)
(1) 软件操作
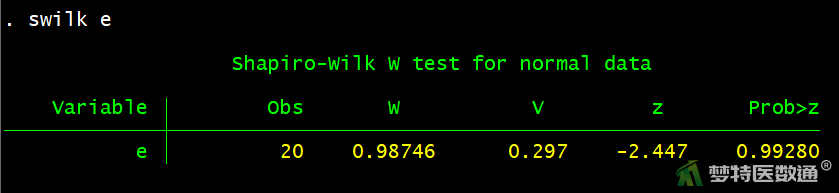
采用Shapiro-wilk检验对残差进行正态性检验,语句如下,结果见图5。
swilk e
(2) 结果解读
正态性检验结果(图5)显示W=0.9875,P=0.9928>0.05,提示因变量残差近似服从正态分布。本案例满足条件5。
4. 条件6判断(异常值检测)
(1) 软件操作
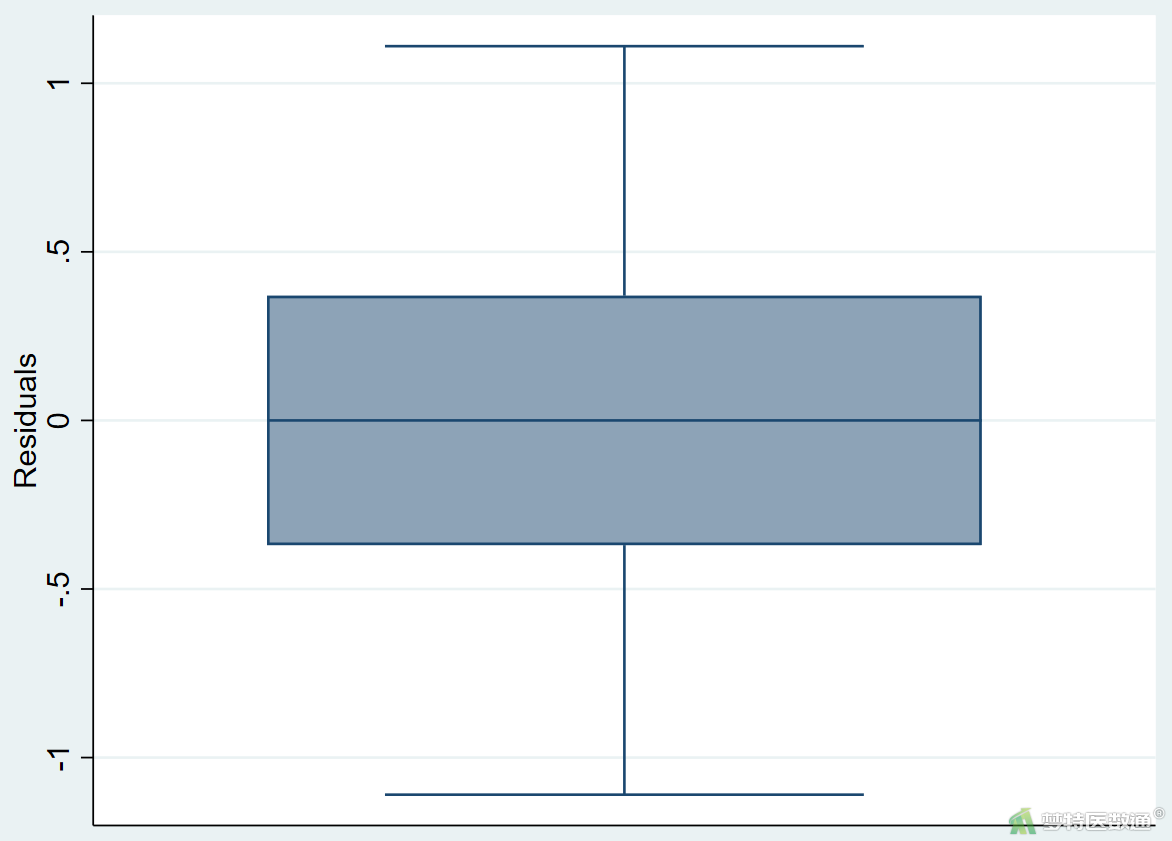
绘制箱线图对残差进行异常值检测,语句如下,结果见图6。
graph box e
(2) 结果解读
箱线图(图6)未提示任何异常值和极端值,满足条件6。
(三) 统计描述
1. 软件操作
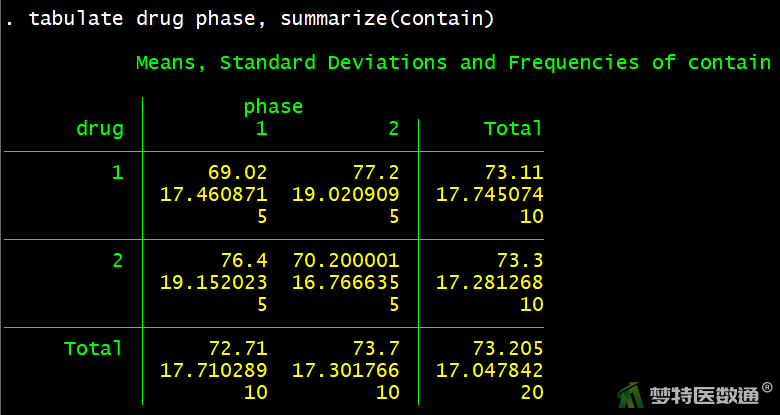
tabulate drug phase, summarize(contain) bysort drug: summarize contain bysort phase: summarize contain
2. 结果解读
由图7可知,第一阶段A、B药物组的血浆浓度分别为69.02±17.46、76.40±19.15 mmol/L,第二阶段A、B药物组的血浆浓度分别为77.20±19.02、70.20±16.77 mmol/L。
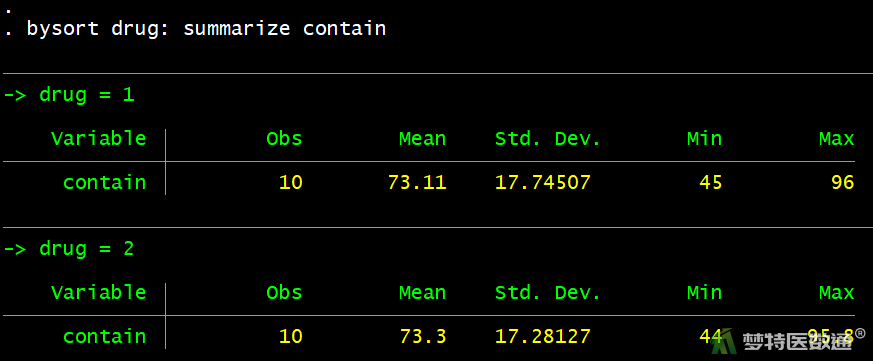
由图8可知,A、B药物组总体的血浆浓度分别为73.11±17.75、73.30±17.28 mmol/L。
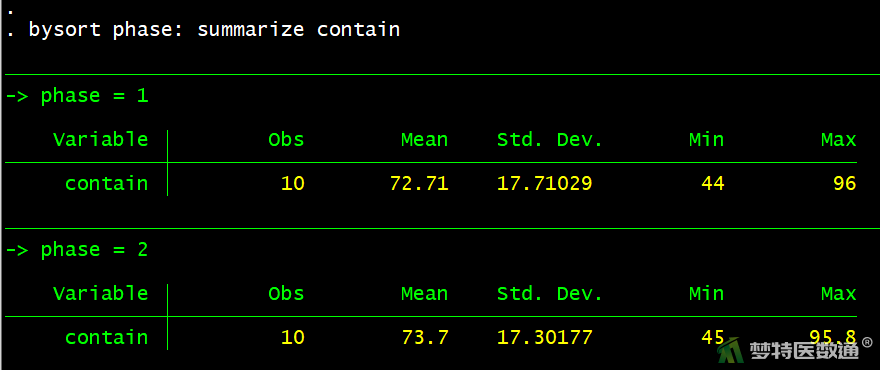
由图9可知,第一阶段、第二阶段总体的血浆浓度分别为72.71±17.71、73.70±17.30 mmol/L。
(四) 三因素方差分析
1. 软件操作
anova contain testid drug phase
2. 结果解读
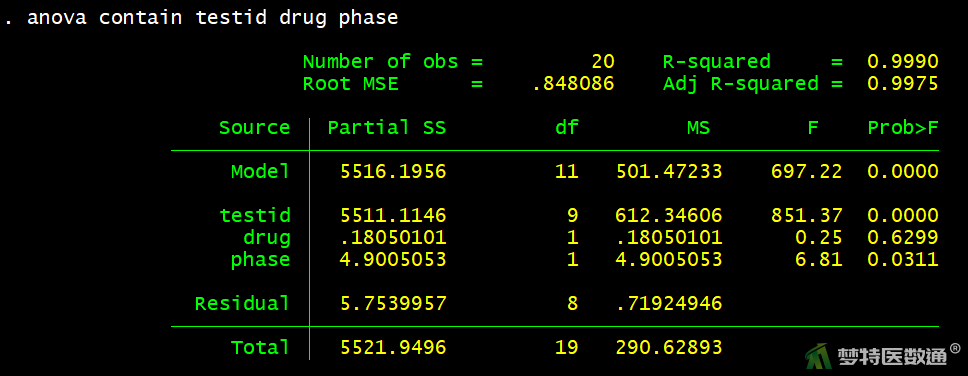
两阶段交叉设计的方差分析结果见图10。药物的Fdrug=0.25,Pdrug=0.630;表明尚不能认为两种药物的血浆浓度有差别。阶段的Fphase=6.81,Pphase=0.031,表明两阶段血浆浓度差异有统计学意义。样本编号的Ftestid=851.37,Ptestid<0.001,表明个体间血浆浓度差异有统计学意义。
四、结论
本研究采用交叉设计分析A、B两种药物对某指标的血浆浓度的影响。计算残差后,通过对残差进行方差齐性检验,提示数据方差齐;通过对残差进行正态性检验,提示数据服从正态分布;通过绘制箱线图,提示数据不存在需要特殊处理的异常值。
分析结果显示,A、B药物组总体的血浆浓度分别为73.11±17.75、73.30±17.28 mmol/L,第一阶段、第二阶段总体的血浆浓度分别为72.71±17.71、73.70±17.30 mmol/L。两种药物的血浆浓度差异无统计学意义(F=0.25,P=0.630);两阶段血浆浓度差异有统计学意义(F=6.81,P=0.031)。