关键词:两因素方差分析; 交互作用; 主效应; 单独效应; 简单效应
一、适用条件
两因素方差分析,需要满足6个条件:
条件1:观察变量唯一,且为连续变量。
条件2:有两个分组变量,且都为分类变量。
条件3:观测值相互独立。
条件4:观察变量不存在显著的异常值。
条件5:各组、各水平观察变量为正态(或近似正态)分布。
条件6:相互比较的各处理水平(组别)的总体方差相等,即通过方差齐性检验。
二、统计量计算
本部分以两因素两水平的析因设计为例,介绍两因素方差分析的统计量计算。

两因素方差分析可以首先按照单因素方差分析的方法把变异分为总变异SS总、组间变异SS组间、组内变异SS组内,具体参考“单因素方差分析(One-way ANOVA)——理论介绍”。
其中,组间变异SS组间可进一步分解为A因素主效应的离均差平方和SSA,B因素主效应的离均差平方和SSB,与AB交互作用的离均差平方和SSAB三部分,见图2。其中,T1,T2,T3,T4分别为(a1b1),(a1b2),(a2b1),(a2b2);A1,A2,B1,B2分别为(T1+T2),(T3+T4),(T1+T3),(T2+T4);n= n1= n2= n3= n4=各组例数。
单独效应是指其他因素的水平固定时,同一因素不同水平间的差别。如图1中,当A因素固定在1水平时,B因素的单独效应为(a1b2)-(a1b1)。
主效应是指某一因素各水平间的平均差别。如图1中,B因素水平为1时,A因素的单独效应为(a1b1)-(a2b1);B因素固定为2时,A因素的单独效应为(a1b2)-(a2b2),平均后的A因素的主效应为[(a1b1)-(a2b1)+(a1b2)-(a2b2)]/2。
交互作用是指当因素的各个单独效应随另一因素变化而变化。如图1中,A与B的交互作用表示为AB=[(a2b2-a1b2)-(a2b1-a1b1)]/2。若存在交互作用,在统计分析时须逐一分析各因素的单独效应。反之,若不存在交互作用,说明两因素的作用效果相互独立,逐一分析各因素的主效应即可。

三、案例数据
研究A、B两种镇痛药物联合运用在癌症患者的镇痛效果。A药取3个剂量:1.0、2.5、5.0 mg;B药也取3个剂量:5、15、30 μg,共9个处理组。将27名研究对象随机分成9组,每组3名,记录每名对象的镇痛时间Time (min)。试分析A、B两药联合运用的镇痛效果。数据见图3。
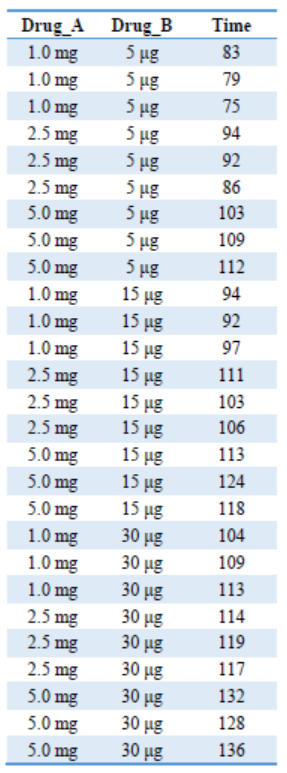
四、假设检验
(一) 正态性检验
两因素方差分析中,有两种选择来检验正态性(参考“方差分析的基本思想和应用条件”)。本例既可以检验各组、各水平数据的正态性,也可以检验因变量残差的整体正态性,采用后者分析结果如图4和图5所示。
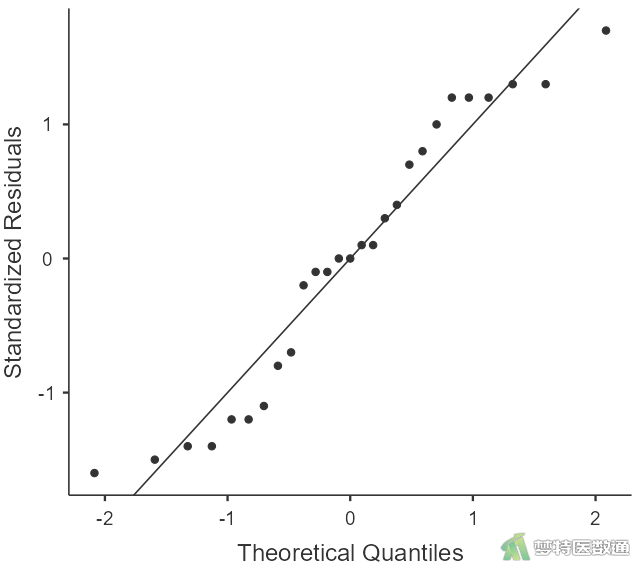

图4的Q-Q图上散点基本围绕对角线分布,提示因变量残差呈近似正态分布;图5为对因变量残差的正态性检验分析结果,P=0.090,提示残差近似服从正态分布。综上,本案例满足正态性条件。
(二) 方差齐性检验
此处使用Levene检验进行方差齐性检验,结果如图6所示。

由图6的“Homogeneity of Variance Test (Levene's) (Levene's方差齐性检验)”结果可知,F=0.304,P=0.955,提示相互比较的各处理水平(组别)的总体方差齐。
(三) 交互作用判断
1. 建立检验假设,确定检验水准
H0:A、B两因素交互作用等于0,即A药物和B药物不存在交互作用
H1:A、B两因素交互作用不等于0,即A药物和B药物存在交互作用
α = 0.05
2. 计算检验统计量
由图2公式和图3数据可得图7分析结果:
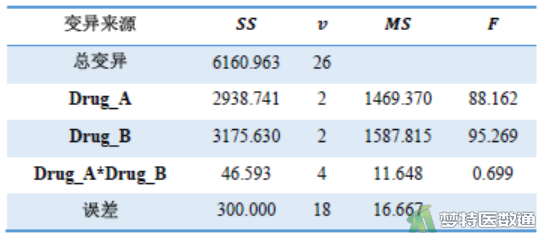
3. 确定P值,作出推断结论
图7中,A、B的交互作用F=0.699< F0.05(4, 18)= 2.93,P>0.05,不拒绝H0,A、B之间的交互作用不具有统计学意义。
(四) 两因素方差分析(主效应分析)
由于A、B药物之间不存在交互作用,说明两因素的作用效果相互独立,逐一分析各因素的主效应即可。
1. 建立检验假设,确定检验水准
A药物主效应:
H0:三个总体均数全相等,即A药物的三个水平对癌症患者的镇痛效果相等
H1:三个总体均数不全相等,即A药物的三个水平对癌症患者的镇痛效果不全相等
B药物主效应:
H0:三个总体均数全相等,即B药物的三个水平对癌症患者的镇痛效果相等
H1:三个总体均数不全相等,即B药物的三个水平对癌症患者的镇痛效果不全相等
2. 计算检验统计量
尽管A、B因素的交互作用无统计学意义,但计算主效应时,在模型中仍需要保留交互项。 因此计算结果和图7一致。
3. 确定P值,作出推断结论
对于Drug_A,F= 88.162>F0.05(2, 22)=3.44,P<0.05,按α=0.05水准,拒绝原假设,差异有统计学意义,即不能认为A药物的三个水平对癌症患者的镇痛效果相等。对于Drug_B,F= 95.269>F0.05(2, 22)=3.44,P<0.05,按α=0.05水准,拒绝原假设,差异有统计学意义,即不能认为B药物的三个水平对癌症患者的镇痛效果相等。