前面介绍了两个样本均数比较的t检验方法,本部分介绍多个样本均数比较的方差分析方法。方差分析的用途很广,本部分仅介绍单因素方差分析、单因素协方差分析、两因素方差分析、单因素重复测量方差分析和两因素重复测量方差分析。本文介绍方差分析的基本思想和应用条件。
关键词:方差分析理论; 方差分析的基本思想; 方差分析的应用条件
一、基本思想
科学研究时,通常要根据研究设计将所研究的对象随机分为多个组并施加不同的处理因素(treatment factor),又称为干预。处理因素的不同取值称为水平(level),一般至少有两个水平。这类科研资料的统计分析,是通过所获得的样本均数信息来推断各组所代表的总体均数差别是否有统计学意义,即因素有无效果或因素的不同水平之间有无差别。常采用的统计分析方法为方差分析(analysis of variance,ANOVA)。此法由英国统计学家R.A.Fisher首创,故方差分析又以Fisher的首字母命名为F检验。下面结合单个因素的完全随机设计,介绍方差分析的基本思想。
设研究因素有g (g≥2)个不同的水平,研究对象随机分为g组,分别接受不同水平的干预,第i (i=1, 2, …,g)组的样本含量为ni,第i组的第j (j=1, 2, …,ni)个观测值用Xij表示。实验结果可整理为图1形式。方差分析的目的就是在H0 (µ1=µ2=…µg)成立的条件下,通过分析各组均数\(\bar{X}_{i}\)之间的差别大小,推断g个总体均数间有无差别,从而说明研究因素的效果是否存在。
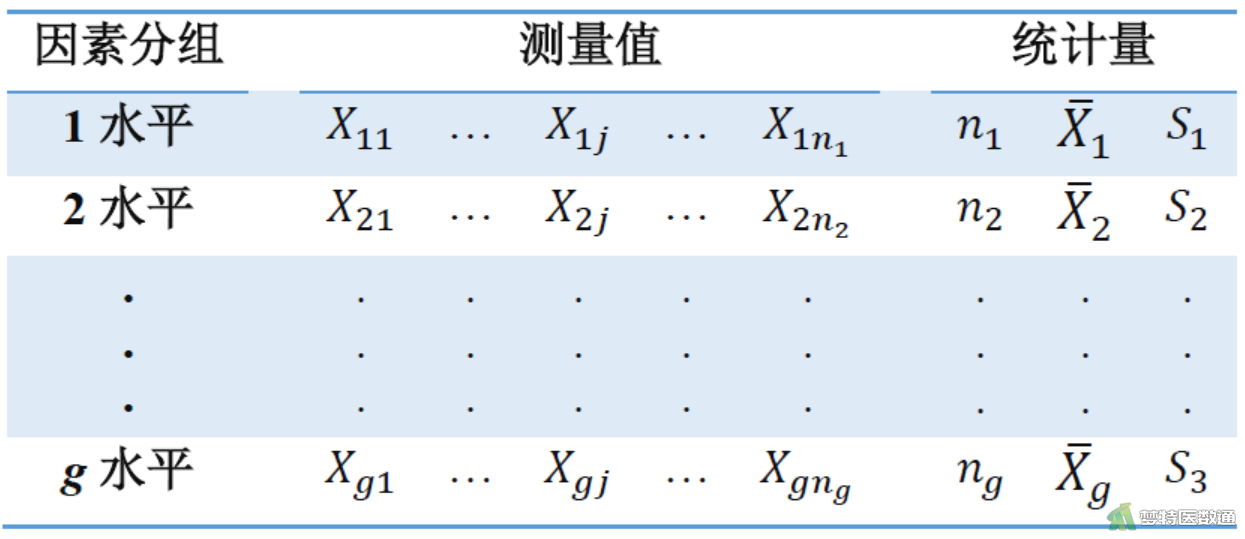
总均数记为 \( \bar{X}=\sum_{i=1}^{g} \sum_{j=1}^{n_{i}} X_{i j} / N\),各组均数为 \( \bar{X}_{i}=\sum_{j=1}^{n_{i}} X_{i j} / n_{i}\),总例数为N=n1+ n2+…+ ng,g为组数。
实验数据有三种不同的变异。
(一) 总变异
全部观测值大小不同,这种变异称为总变异。总变异的大小可以用离均差平方和(sum of squares of deviations from mean)表示,即各观测值Xij与总均数\(\bar{X}\)差值的平方和,记为SS总。总变异SS总反映了所有观测值之间总的变异程度,计算公式为
\( SS_总=\sum_{i=1}^g\sum_{j=1}^{n_i}(X_{ij}-\bar{X})^2=\sum_{i=1}^g\sum_{j=1}^{n_i}X_{ij}^2-C\)其中, \( C=\left(\sum_{i=1}^{g} \sum_{j=1}^{n_{i}} X_{i j}\right)^{2} / N\)。
(二) 组间变异
各组由于接受处理因素的水平不同,各组的样本均数 \( \bar{X}_{i}(i=1,2, \ldots, g) \) 也大小不等,这种变异称为组间变异。存在组间变异的原因有:(1)随机误差(包括个体变异和测量误差,测量误差常忽略不计);(2)处理因素的不同水平可能对实验结果的影响。其大小用各组均数\(\bar{X}_{i}\)代替原始数据后与总均数 \( \bar{X}\)的离均差平方和表示,记为SS组间,计算公式为:
\( SS_{组间}=\sum_{i=1}^gn_i(\bar{X}_i-\bar{X})^2=\sum_{i=1}^g\frac{\left(\sum_\limits{j=1}^{n_i}X_{ij}\right)^2}{n_i}-C\)各组均数 \(\bar{X}_{i}\)之间相差越悬殊,它们与总均数 \( \bar{X}\)的差值越大,SS组间就越大;反之SS组间越小。SS组间反映了各 \( \bar{X}_{i}\)间的变异程度。
(三) 组内变异
在同一组中,虽然每个受试对象接受的处理因素水平相同,但观测值仍各不相同,这种变异称为组内变异(误差)。组内变异为组内各观测值Xij与其所在组的均数\(\bar{X}_{i}\)的差值的平方和,记为SS组内,表示随机误差的影响。计算公式为: \( SS_{组内}=\sum_{i=1}^g\sum_{j=1}^{n_i}(X_{ij}-\bar{X})^2\)
各离均差平方和的自由度为:
υ总 = N-1,υ组间 = g-1,υ组内 = N-g
总离均差平方和分解为组间离均差平方和与组内离均差平方和,即
SS总 = SS组间 + SS组内
相应地,总自由度分解为组间自由度与组内自由度,有
υ总 =υ组间 +υ组内
变异程度除与离均差平方和的大小有关外,还与其自由度有关。由于各部分自由度不相等,故各部分离均差平方和不能直接比较,须将各部分离均差平方和除以相应的自由度,其比值称为均方差,简称均方(mean square, MS)。组间均方和组内均方的计算公式为
\( M S_{\text {组间 }}=\frac{S S_{\text {组间 }}}{v_{\text {组间 }}}\) \( M S_{\text {组内 }}=\frac{S S_{\text {组内 }}}{v_{\text {组内 }}}\)如果各组样本的总体均数相等(µ1=µ2=…µg),即各组的样本来自相同总体,即因素无作用,则组间变异同组内变异一样,只反映随机误差作用的大小。组间均方与组内均方的比值称为F统计量。
\( F=\frac{M S_{\text {组间 }}}{M S_{\text {组内 }}}, v_{1}=v_{\text {组间 }}, v_{2}=v_{\text {组内 }}\)如果F接近于1,就没有理由拒绝H0;反之,F越大,拒绝H0的理由越充分。
数理统计理论证明:当H0成立时,F统计量服从F分布。方差分析是单侧F检验,由(F界值表),可查出按α水准(一般取α=0.05)F分布的单尾界值 \( F_{\alpha,\left(v_{1} \cdot v_{2}\right)}\),作为判断统计量F大小的标准。若根据实验结果计算的F偏大,如F≥ \( F_{\alpha,\left(v_{1} \cdot v_{2}\right)}\),则P≤0.05,拒绝H0,接受H1:µi不全相等(i=1,2,¼,g),说明各样本来自不全相同的总体,即认为各总体均数不全相等,表明干预因素不同水平的作用不全相同。反之,当F< \( F_{\alpha,\left(v_{1} \cdot v_{2}\right)}\),则 P>0. 05,不拒绝H0,尚不能作出各总体均数有差别的结论。
综上所述,方差分析的基本思想就是根据研究设计的类型,将全部观测值总的离均差平方和及其自由度分解为两个或多个部分,除随机误差作用外,每个部分的变异可由某个因素的作用(或某几个因素的交互作用)加以解释,如组间变异SS组间可由研究因素的作用加以解释。通过比较不同变异来源的均方,借助F分布作出统计推断,从而推论研究因素对研究结果有无影响。
多个样本均数比较的方差分析方法与实验设计类型密切相关。方差分析的数据是按照特定实验设计进行实验所得的数据,不同的实验设计其总变异的分解有所不同。因此在应用方差分析时,除要求资料满足方差分析的应用条件外,还应结合具体实验设计来选择相应的方差分析方法。
二、应用条件
多个样本均数比较的方差分析其应用条件为:
条件1:各样本是相互独立的随机样本,即满足独立性(independence)。
条件2:各样本来自正态分布总体,即满足正态性(normality)。
在方差分析中,有两种选择来检验正态性。如果每个分组有很多观测值,那么可以检验每组观测值的正态性。但是,如果数据有很多分组,或者每个组的观察值很少,那么检验整体残差的正态性通常更容易。这是因为方差分析对数据的非正态性有一定的耐受力。如果在模型中有一个协变量为连续变量,则只能检验残差的正态性。如果样本的残差偏离正态,需作数据转换,改善其正态性或选用其他统计分析方法。
条件3:各样本的总体方差相等,即具有方差齐性(homogeneity of variance)。
对方差齐性的判断常采用方差齐性检验(homogeneity of variance test)的方法,检验多个样本所代表的总体方差是否不等,可采用的方法有Bartlett χ2和Levene检验。