协方差分析(Analysis of Covariance，ANCOVA)——理论介绍

发布于 2021年7月29日星期四 16:51:31 浏览：38259

原创不易，转载请注明来源，感谢！

协方差分析(analysis of covariance，ANCOVA)是将线性回归分析与方差分析结合起来的一种统计分析方法，用于比较两组或多组均数之间的差异时，控制对因变量有影响的混杂因素(即协变量covariate)的一种方法。协变量可以有一个、两个或多个，分析方法略有不同，但其解决问题的基本思想相同。

关键词：协方差分析; 单因素协方差分析; 平行性检验; 平行线检验

一、适用条件

协方差分析，需要满足9个条件：

条件1：观察变量为连续变量。

条件2：观测值相互独立。

条件3：观察变量不存在显著的异常值。

条件4：自变量存在2个或多个分组。

条件5：协变量是连续变量。

条件6：各组内因变量的残差服从正态(或近似正态)分布。

条件7：组间因变量的残差方差齐。

条件8：各组内协变量和观察变量之间存在线性关系。

条件9：各组内协变量和因变量的回归直线平行，即通过平行性检验。

二、统计量计算

协方差分析是将线性回归与方差分析相结合的一种分析方法。把对因变量Y有影响的因素X看作协变量，建立Y对X的线性回归，利用回归关系把X值化为相等，再进行各组Y的修正均数间比较。修正均数是假设各协变量取值固定在其总均数时的观察变量Y的均数。协方差其实质是从Y的总离均差平方和\(\sum(Y-\bar{Y})^{2}\)中，扣除协变量X对Y的回归平方和\(\sum(\hat{Y}-\bar{Y})^{2}\)，对残差平方和\(\sum(Y-\hat{Y})^{2}\)作进一步分解后再进行方差分析。

残差平方和的分解：

\(\sum(Y-\hat{Y})_{\text {总 }}^{2}=\sum(Y-\hat{Y})_{\text {修正均数间 }}^{2}+\sum(Y-\hat{Y})_{\text {组内 }}^{2}\)

\(v_{\text {总 }}=v_{\text {修正均数间 }}+v_{\text {组内 }}\)

\(F=\frac{M S_{\text {修正均数间 }}}{M S_{\text {组内 }}}=\frac{\sum(Y-\hat{Y})_{\text {修正均数间 }}^{2} / v_{\text {修正均数间 }}}{\sum(Y-Y)_{\text {组内 }}^{2} / v_{\text {组内 }}}\)

其中，\(\sum(Y-\widehat{Y})^{2}=L_{Y Y}-L_{X Y}^{2} / L_{X X}\)

三、案例数据

为研究A、B、C三种饲料对增加小鼠体重的影响，将初始体重相近的45只小鼠随机分成三组，分别喂养A、B、C三种饲料，但在实验设计时未对小鼠的进食量加以限制，现测得三组小鼠的进食量(Food)和所增体重(Weight)，请推断A、B、C三种饲料对小鼠的增重效果是否有差别？部分数据见图2

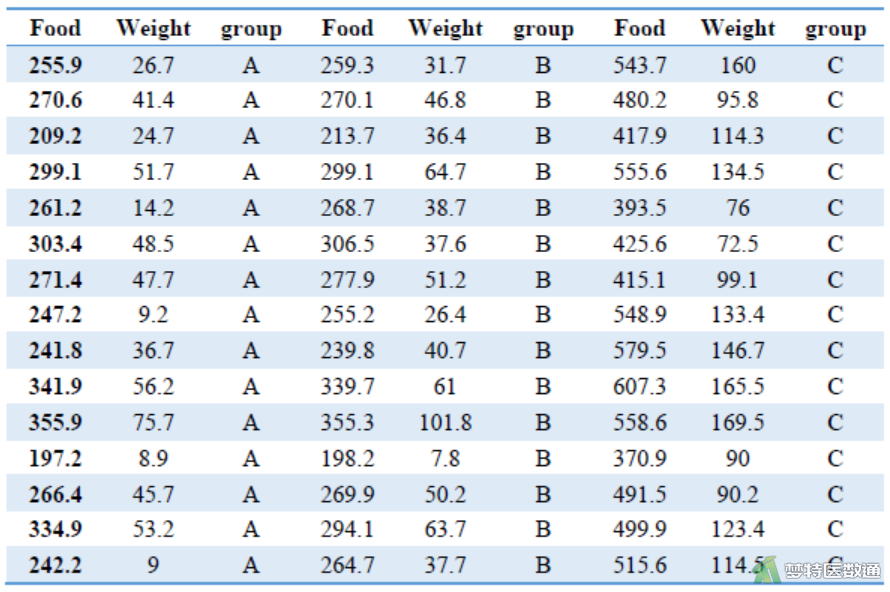
四、假设检验

(一) 正态性检验

在方差分析中，有两种选择来检验正态性(参考“方差分析的基本思想和应用条件”)。本例中含有一个连续的协变量，因此需要检验因变量残差整体的正态性。采用jamovi软件检验因变量残差整体的正态性，结果如图3所示。

由图3的正态性检验结果可知，P=0.806>0.1，提示残差服从正态分布。综上，本案例满足正态性条件。

(二) 方差齐性检验

此处使用Levene检验进行方差齐性检验，由于该检验的计算量巨大，使用jamovi软件完成计算过程，结果如图4所示。

由图4的“Homogeneity of Variance Test (Levene’s) (Levene’s方差齐性检验)”结果可知，F=2.066，P=0.139，提示本案例组间因变量残差的方差齐。

(三) 线性关系检验

分别绘制各组Food与Weight的散点图并计算相关系数，可判断各组内协变量和因变量之间是否存在线性关系。绘制散点图和计算相关系数使用jamovi软件完成，结果如图5和图6所示。

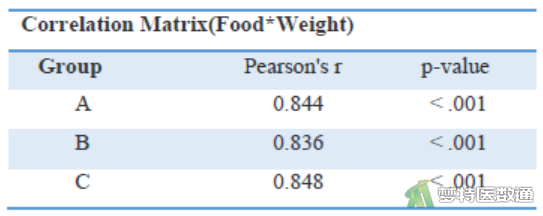
由图5可知，A、B、C三组内“Food”与“Weight”均呈现线性关系；图6“Correlation Matrix (相关矩阵)”分析列出了详细的相关性检验结果，可见相关系数均较高(>0.8)，P值均<0.001。综上，本案例各组内协变量和因变量之间均存在线性关系。

(四) 平行性检验

平行性检验通过判断group与Food的交互项是否有统计学意义决定。使用jamovi软件完成计算过程，结果如图7所示。

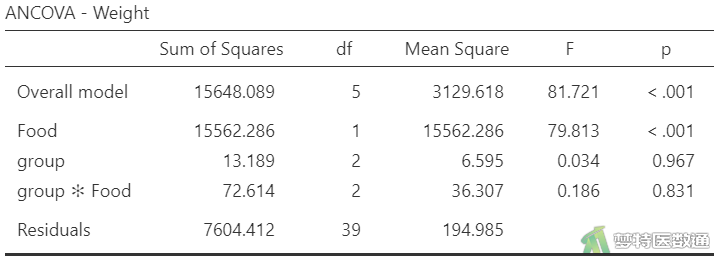
在图7“ANCOVA – Weight (单因素协方差分析)”表格中，“Overall model (整体模型)”列的F_overall =81.721，P_overall <0.001，表示整体模型检验具有统计学意义。“group*Food”的交互项检验结果为F_group*Food =0.186，P_group*Food=0.831，表示交互项无统计学意义，即满足平行性检验。