单因素重复测量资料是同一受试对象的同一观察指标在不同时间点上进行多次测量所获得的资料,常用来分析该观察指标在不同时间点上的变化特点。这种类型的资料在医学实验研究中非常常见。重复测量资料的多次测量数据之间往往存在一定相关性,因此,这类资料的方差分析也有其特殊性。本文介绍单因素重复测量方差分析(One-Way Repeated Measures ANOVA)的适用条件及假设检验理论。
关键词:重复测量; 重复测量资料; 重复测量方差分析; 单因素重复测量方差分析; 球形检验; 交互作用; 主效应; 单独效应
一、适用条件
单因素重复测量方差分析,需要满足6个条件:
条件1:观察变量唯一,且为连续变量。
条件2:观察变量为重复测量数据,即不满足独立性。
条件3:观察变量不存在显著的异常值。
条件4:各水平(时间点)观察变量为正态(或近似正态)分布。
条件5:各重复测量水平观察变量的协方差相等,即满足球形假设。
二、统计量计算
单因素重复测量资料的总变异可以分为两部分,一部分为区组间的变异,另一部分为区组内的变异。其中区组内的变异又分为个体间的变异和误差两部分。单因素重复测量方差分析变异来源如图1所示。

其中,n为受试对象的个数,k为重复测量的次数(1,2,…,i),G为所有观测值的总和,T为每一个试点的观测值总和,P为每一个受试对象的观测值总和。
三、案例数据
检验科研究血样放置时间对某生化指标浓度检测的影响,采集了10份人体血液标本,分别在放置0分钟(T0)、30分钟(T30)、60分钟(T60)和90分钟(T90)时对该指标的浓度(mmol/L)进行检测,分析放置时间是否对该生化指标检测结果有影响?数据见图1。
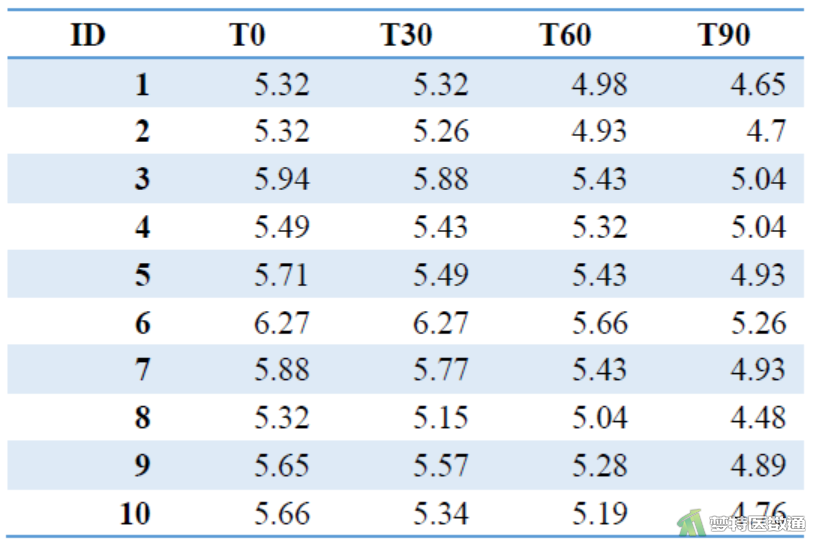
四、假设检验
(一) 正态性检验
单因素重复测量方差分析时,需要检测各水平(时间点)观察变量的正态性。采用jamovi软件分析结果如图2所示。
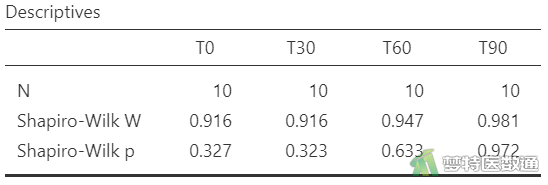
图3的正态性检验结果显示各时间点的P值为0.327、0.323、0.633、0.972,均>0.1,提示四组数据服从正态分布。此外,本案例也可以绘制Q-Q图,结果也提示四组数据服从正态分布。
(二) 球形假设检验
球对称性通常采用 Mauchly检验(Mauchly's test)来判断。采用jamovi软件分析结果如图3所示。

由图4的“Tests of Sphericity (球形检验)”结果可知,W=0.252,P=0.061,>0.05,表示满足球形假设,此时无须对区组内效应的F界值进行矫正。
(三) 单因素重复测量方差分析
1. 建立检验假设,确定检验水准
H0:血样放置时间对该生化指标浓度检测影响相同
H1:血样放置时间对该生化指标浓度检测影响不同
α = 0.05
2. 计算检验统计量
由图1公式和图2 数据可得图5计算结果:

3. 确定P值,作出推断结论
根据图5中的统计量,F= 116.103>F0.05(3, 27)= 2.96,则P<0.05,按α=0.05检验水准,拒绝原假设,差异有统计学意义。即不能认为血样的放置时间对生化指标浓度检测影响相同。