单因素方差分析(One-way ANOVA),又称完全随机设计的方差分析,是指采用完全随机化的分组方法,是将受试对象随机地分配到各个处理组,再比较各组均数之间的差别有无统计学意义,推论处理因素的效应。本篇文章举例介绍单因素方差分析的适用条件及假设检验。
关键词:单因素方差分析; F检验; Welch检验; 韦尔奇检验; 事后检验; 两两比较
一、适用条件
单因素方差分析,需要满足6个条件:
条件1:观察变量为连续变量。
条件2:观测值相互独立。
条件3:观测值可分为多组(≥2)。
条件4:观察变量不存在显著的异常值。
条件5:各组观测值为正态(或近似正态)分布。
条件6:多组观测值的整体方差相等。
二、统计量计算
(一) 单因素方差分析
当多组观察变量的整体方差相等时,即满足方差齐性时,可采用F检验进行单因素方差分析。当多组观察变量的整体方差不相等时,即不满足方差齐性时,可通过变量变换达到方差齐性要求,或者采用校正的单因素方差分析法(Welch检验)进行比较。
1. F检验
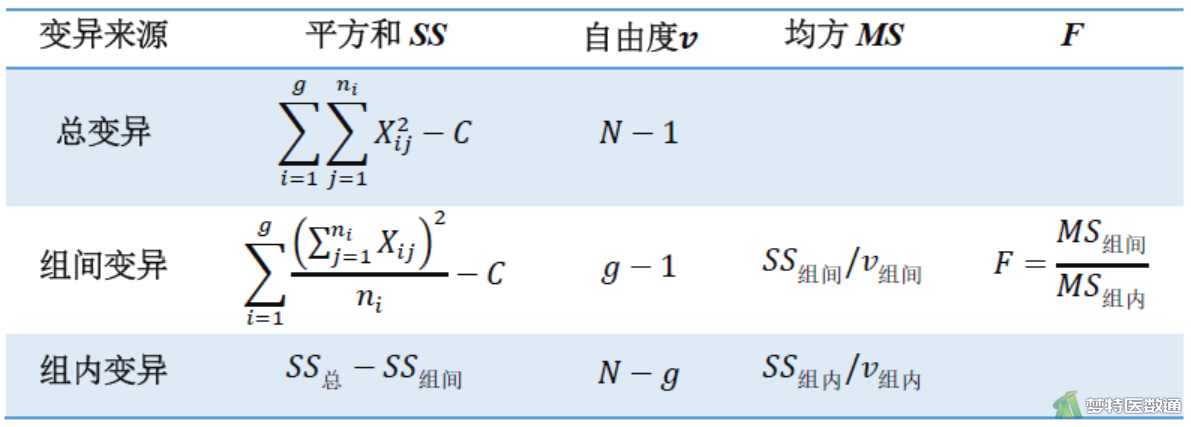
单因素方差分析的总变异可拆分为组间变异和组内变异两部分:
SS总=SS组间+SS组内,υ总=υ组间+υ组内
方差分析计算公式见图1,表中校正数C= \( \left(\sum_{i=1}^{g}\sum_{j=1}^{n_{i}} X_{i j}\right)^{2}/N\) ,N为样本量,g为处理组数。
2. Welch检验
Welch检验是指采用Welch分布的统计量检验各组均值是否相等。Welch分布近似于F分布,采用Welch检验对方差齐性没有要求,所以当数据的分布不满足方差齐性的要求时,采用Welch检验比F检验更稳妥。其计算公式如下:
\( F=\frac{\frac{1}{k-1} \sum_{j=1}^{k} \mathrm{w}_{j}\left(\bar{x}_{j}-\bar{x}^{\prime}\right)^{2}}{1+\frac{2(k-2)}{k^{2}-1} \sum_{j=1}^{k}\left(\frac{1}{n_{j}-1}\right)\left(1-\frac{w_{j}}{w}\right)^{2}} \)其中, \( w_{j}=\frac{n_{j}}{s_{j}^{2}},w=\sum_{j=1}^{k} w_{j} \) , \( \bar{x}^{\prime}=\frac{\sum_{j=1}^{k} w_{j} \overline{x_{j}}}{w} \) ,k为处理组数。
F~F(k-1, df)
自由度: \( d f=\frac{k^{2}-1}{3 \sum_{j=1}^{k}\left(\frac{1}{n_{j^{-1}}}\right)\left(1-\frac{w_{j}}{w}\right)^{2}} \)
(二) 多个样本均数的两两比较
单因素方差分析整体比较,推断结论为拒绝H0,接受H1时,只能认为各总体均数之间整体比较有差异,但尚不能说明任意两个总体均数之间都有差别。若要进一步推断具体哪两个总体均数有差别,需要进一步事后检验(两两比较)。多个样本均数比较的事后检验可分为两种情况,一是各组间均要相互比较,以了解任何两组间是否有差别;二是仅考虑某指定组与其它各组比较,例如有一组为对照组,意欲了解其它各实验组与该对照组间是否有差别。多重比较的方法很多,这里介绍三种方法,即适用于多组间两两比较的 SNK法 (q检验),适用于某指定组与其它各组比较的Dunnett-t法(q'检验),以及适用于方差不齐时多组间两两比较的Games-Howell法。
1. SNK法
SNK法(Student-Newman-Keuls)用于比较每两个样本均数所代表的总体均数是否不同,其检验统计量为q,又称q检验。
\( q=\left(\bar{X}_{A}-\bar{X}_{B}\right) / \sqrt{\frac{M S_{\text {误差 }}}{2} \times\left(\frac{1}{n_{\mathrm{A}}}+\frac{1}{n_{\mathrm{B}}}\right)} \)式中 \( \bar{X}_{A} \) 、 \( \bar{X}_{B} \) 为两对比组的样本均数,MS误差为方差分析中算得的误差均方(或称组内均方),nA和nB分别对两对比组样本例数。
2. Dunnett-t法
Dunnett-t法适用于多个实验组与一个对照组间的两两比较,其检验统计量为q',又称q'检验。
\( q^{\prime}=\frac{\left|\bar{X}_{T}-\bar{X}_{C}\right|}{\sqrt{M S_{\text {误差 }}\left(\frac{1}{n_{T}}+\frac{1}{n_{C}}\right)}} \)上式中 \( \bar{X}_{T} \) 与nT为实验组均数和样本例数, \( \bar{X}_{C} \) 与nC为对照组均数和样本例数。算得q'值后需查(q'界值表)。(q'界值表)中的υ仍为方差分析中误差项的自由度,a仍为两对比组包含的组数。
3. Games-Howell法
Games-Howell法适用于方差不齐时多组间的两两比较。这种方法背后的理念是关注两组平均值之间差异的最大值。其统计量计算为:
\( \text { s.e. }=\sqrt{\frac{1}{2} \cdot\left(\frac{s_{i}^{2}}{n_{i}}+\frac{s_{j}^{2}}{n_{j}}\right)} \)n为每组样本量。统计量q的分布称为studentized range q分布。该分布的临界值在基于 α 、k (组数)和dfw值的(studentized range q表)中给出。如果q > qcrit,则两组均值有统计学差异。
此检验相当于
\( \bar{x}_{\max }-\bar{x}_{\min }>q_{\text {crit }} \sqrt{\frac{1}{2} \cdot\left(\frac{s_{i}^{2}}{n_{i}}+\frac{s_{j}^{2}}{n_{j}}\right)},其中 [latex] d f^{\prime}=\frac{\left(\frac{s_{i}^{2}}{n_{i}}+\frac{s_{j}^{2}}{n_{j}}\right)^{2}}{\left.\frac{\left(\frac{s_{i}^{2}}{n_{i}}\right)^{2}}{n_{i}-1}+\frac{s_{j}^{2}}{n_{j}}\right)^{2}} \)三、案例数据
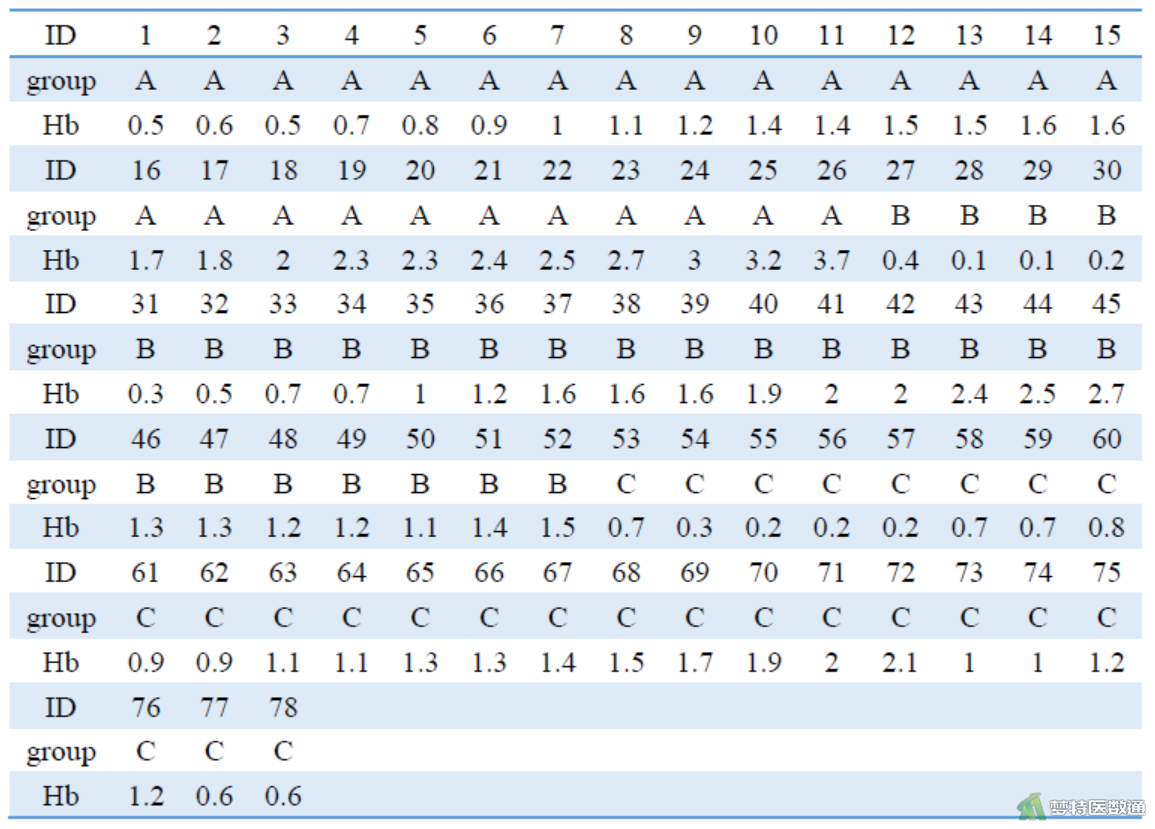
某医生用A、B、C三种方案治疗血红蛋白低下的贫血患者,治疗两个月后,记录每名受试者血红蛋白的上升克数。问3种治疗方案对患者贫血的疗效是否有差别?具体数据见图2。
四、假设检验
(一) 正态性检验
在方差分析中,有两种选择来检验正态性(参考“方差分析的基本思想和应用条件”)。本例中一共有3个分组,每个分组有很多观测值,那么可以检验每组观测值的正态性。本文采用jamovi软件进行数据的正态性检验,具体过程参考“单因素方差分析—jamovi软件实现”,结果如图3和图4所示。
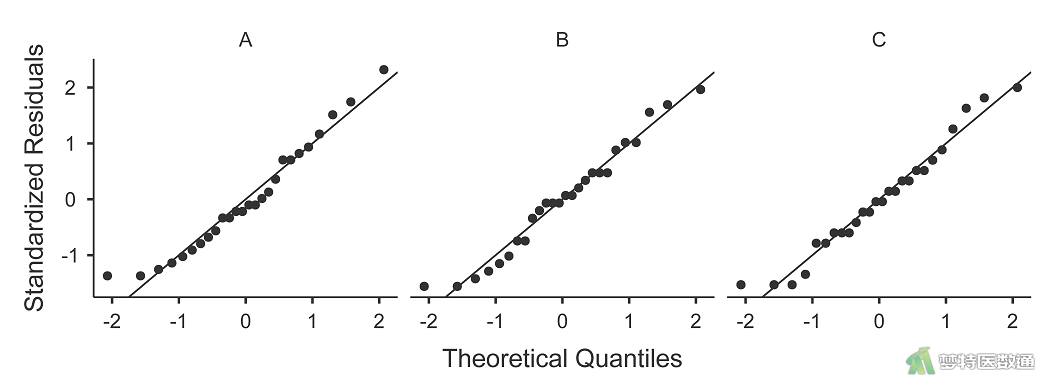
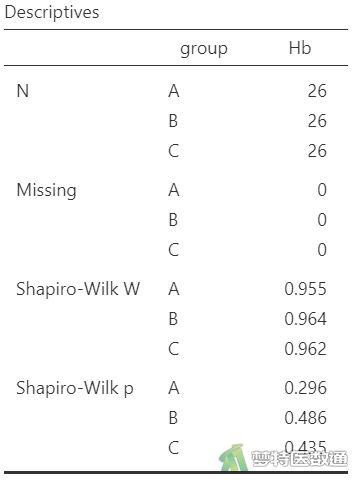
图3和图4按照组别列出了三组的正态性检验结果。图3的Q-Q图上三组散点基本围绕对角线分布,提示三组数据呈正态分布;图4的正态性检验结果分别显示三组的P=0.296、0.486、0.435,均>0.1,也提示三组数据满足正态性条件。综上,本案例满足正态性条件。
(二) 方差齐性检验
此处使用Levene检验进行方差齐性检验,使用jamovi软件完成计算过程,具体操作详见“单因素方差分析—jamovi软件实现”,结果如图5和图6所示。
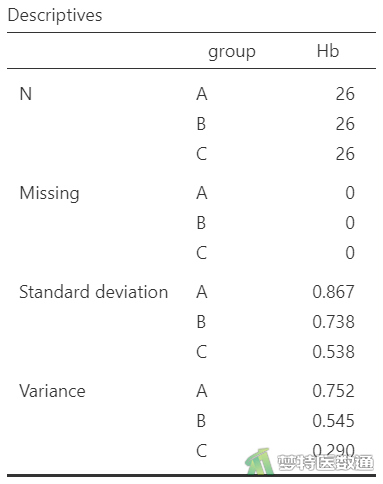

由图5“Descriptives (描述性分析)”表格中“Std. deviation (标准差)”和“Variance (方差)”结果可知,A、B、C三组的标准差分别为0.867、0.738、0.538,方差分别为0.752、0.545和0.290,三组的方差数值存在差异,但还需要依据统计学检验的结果进行判断。
图6“Homogeneity of Variances Test (Levene’s) (Levene’s方差齐性检验)”为方差齐性检验结果,可见F=2.610,P=0.080<0.1,提示三组数据方差不齐,不满足方差齐性的要求。
本案例数据满足正态性要求,不满足方差齐性要求,但方差并非严重不齐,可采用Welch检验进行数据分析。
(三) 单因素方差分析(Welch检验)
1. 建立检验假设,确定检验水准
H0:μ1= μ2= μ3,即三种治疗方案受试者血红蛋白的上升克数相等
H1:三种治疗方案受试者血红蛋白的上升克数不全相等
α = 0.05
2. 计算检验统计量
本案例中A、B、C三组的样本量分别为nA=26、nB=26、nC=26,三组的均数分别为 \(\bar{X}_{A}\) =1.688、 \(\bar{X}_{B}\) =1.250、 \(\bar{X}_{C}\) =1.023,三组的标准差分别为SA=0.867、SB=0.738、SC=0.538。
根据Welch检验统计量计算公式可计算相应参数值为:
\( w=\sum_{j=1}^{k} w_{j}=\frac{n_{A}}{s_{A}^{2}}+\frac{n_{B}}{s_{B}^{2}}+\frac{n_{C}}{s_{C}^{2}}=\frac{26}{0.867^{2}}+\frac{26}{0.738^{2}}+\frac{26}{0.538^{2}}=171.972 \) \( \bar{x}^{\prime}=\frac{\sum_{j=1}^{k} w_{j} \overline{x_{j}}}{w} \) \( =\left(\frac{26}{0.867^{2}} \times 1.688+\frac{26}{0.738^{2}} \times 1.250+\frac{26}{0.538^{2}} \times 1.023\right) / 172.1538 =1.220\) \( F=\frac{\frac{1}{k-1} \sum_{j=1}^{k} w_{j}\left(\bar{x}_{j}-\bar{x}^{\prime}\right)^{2}}{1+\frac{2(k-2)}{k^{2}-1} \sum_{j=1}^{k}\left(\frac{1}{n_{j}-1}\right)\left(1-\frac{w_{j}}{w}\right)^{2}} \) \( =\frac{\frac{1}{3-1} \times\left(\frac{26}{0.867^{2}} \times(1.688-1.220)^{2}+\frac{26}{0.738^{2}} \times(1.250-1.220)^{2}+\frac{26}{0.538^{2}} \times(1.023-1.220)^{2}\right)}{1+\frac{2 \times(3-2)}{3^{2}-1}\left[\left(\frac{1}{26-1}\right) \times\left(1-\frac{2.867^{2}}{171.972}\right)^{2}+\left(\frac{1}{26-1}\right) \times\left(1-\frac{\frac{26}{171.738^{2}}}{172}\right)^{2}+\left(\frac{1}{26-1}\right) \times\left(1-\frac{0.538^{2}}{171.972}\right)^{2}\right]} \)=5.477
df1 = 3-1 = 2,
df2 = \( \frac{k^{2}-1}{3 \sum_{j=1}^{k}\left(\frac{1}{n_{j}-1}\right)\left(1-\frac{w_{j}}{w}\right)^{2}} \)
\( =\frac{3^{2}-1}{3 \times\left[\left(\frac{1}{26-1}\right) \times\left(1-\frac{0.867^{2}}{171.972}\right)^{2}+\left(\frac{1}{26-1}\right) \times\left(1-\frac{0.738^{2}}{171.972}\right)^{2}+\left(\frac{1}{26-1}\right) \times\left(1-\frac{0.538^{2}}{171.972}\right)^{2}\right]} \)=47.981
3. 确定P值,作出推断结论
以df1 =2,df2 =48查(F界值表)得F0.05(2,48)=3.19。本例F=5.477> F0.05(2,48),则P<0.05。按α = 0.05检验水准,拒绝H0,接受H1,差异有统计学意义,表明三种治疗方案受试者血红蛋白的上升克数不全相等。
(四)多个样本均数间的多重比较(Games-Howell法)
方差不齐时,多个均数事后检验两两比较常采用Games-Howell法。
1. 建立检验假设,确定检验水准
H0:μi= μj,即任何两种治疗方案受试者血红蛋白的上升克数相等
H1:μi≠μj,即任何两种治疗方案受试者血红蛋白的上升克数不等
α = 0.05
2. 计算检验统计量
A组与B组治疗方案比较:
\( \bar{x}_{\max }-\bar{x}_{\min }=1.688-1.250=0.438 \) \( \text { s.e. }=\sqrt{\frac{1}{2} \times\left(\frac{s_{i}^{2}}{n_{i}}+\frac{s_{j}^{2}}{n_{j}}\right)}=\sqrt{\frac{1}{2} \times\left(\frac{0.867^{2}}{26}+\frac{0.738^{2}}{26}\right)}=0.158 \) \( d f^{\prime}=\frac{\left(\frac{s_{i}^{2}}{n_{i}}+\frac{s_{j}^{2}}{n_{j}}\right)^{2}}{\frac{\left(\frac{s_{i}^{2}}{n_{i}}\right)^{2}}{n_{i}-1}+\frac{\left(\frac{s_{j}^{2}}{n_{j}}\right)^{2}}{n_{j}-1}} \) \( =\frac{\left(\frac{0.867^{2}}{26}+\frac{0.738^{2}}{26}\right)^{2}}{\frac{\left(\frac{0.738^{2}}{26}\right)^{2}}{26-1}+\frac{\left(\frac{0.738^{2}}{26}\right)^{2}}{26-1}}=48.755 \)基于α = 0.05、k (组数)=3和df '=49的(studentized range q表),可得qcrit=3.418,所以qcrit×s.e.=3.3.418×0.158=0.540。
同理可计算出其他两组的统计量,如图7所示:

3. 确定P值,作出推断结论
根据图7中的统计量,A组和C组相比时, \( \bar{x}_{\max }-\bar{x}_{\min }>q_{\text {crit }} \times \text { s.e. } \) ,可得P<0.05。按α = 0.05水准,拒绝H0,接受H1,差异具有统计学意义,说明A组和C组治疗方案受试者血红蛋白的上升克数不相等。而其余两组 \( \bar{x}_{\max }-\bar{x}_{\min }<q_{c r i t} \times \text { s.e. } \) ,可得P>0.05。按α = 0.05水准,不拒绝H0,差异不具有统计学意义。