Wilcoxon符号秩检验(Wilcoxon signed-rank test)不仅可以用于单个样本中位数和总体中位数比较,还可用于配对样本差值的中位数和0比较。在前面推文中,我们介绍了单个样本中位数和总体中位数比较的单样本Wilcoxon符号秩检验相关理论,这个系列我们将介绍配对样本差值的中位数和0比较的配对样本Wilcoxon符号秩检验(Paired Samples Wilcoxon Signed Rank Test)相关理论及软件实现。
关键词:非参数检验; 秩和检验; 配对样本Wilcoxon符号秩检验; 配对秩和检验
配对样本Wilcoxon符号秩检验,目的是推断配对样本差值的总体中位数是否和0有差别,即推断配对的两个相关样本所来自的两个总体中位数是否有差别。本篇推文将举例介绍配对样本Wilcoxon符号秩检验的适用条件及假设检验理论。
一、适用条件
对于配对设计的连续性变量,可以选用配对t检验或Wilcoxon符号秩检验。配对t检验适用于两组差值近似服从正态分布的数据。当不满足该条件时,可选择Wilcoxon符号秩检验。对于配对设计的有序分类变量比较,应使用Wilcoxon符号秩检验。使用Wilcoxon 符号秩检验时,需要满足三个条件:
条件1:观察变量是连续变量或有序分类变量。
条件2:观察变量可分为2组。
条件3:观察变量的数据结构为配对形式。
二、统计量计算
(一) 配对设计的连续性变量比较
详见单样本Wilcoxon符号秩检验(One Sample Wilcoxon Signed Rank Test)——理论介绍。
(二) 配对设计的有序分类变量比较
Wilcoxon符号秩检验用于配对的等级资料,需要先把等级从弱到强转换成秩(1,2,3,…);然后求各对秩的差值,省略所有差值为0的对子,令余下的所有有效对子数为n,最后按n个差值编正秩和负秩,求正秩和负秩和。但对于等级资料,相同秩多时小样本的结果会存在偏性,最好用大样本。
三、案例数据
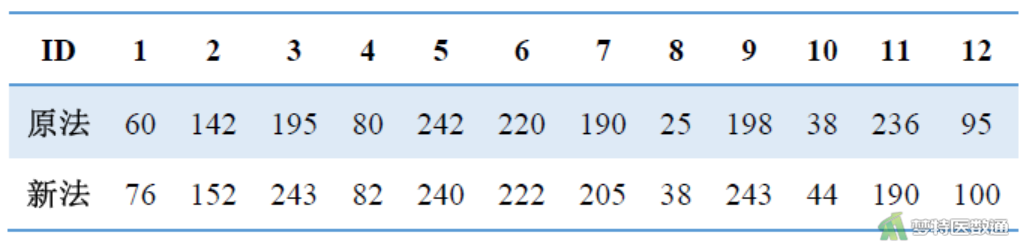
对12份血清分别用原方法(检测时间15分钟)和新方法(检测时间10分钟)测谷草转氨酶,问两种方法所得结果是否有差别?数据见图1。
四、假设检验
配对设计的连续性变量比较,需要检验两组差值的正态性。本例中两组差值经“Normality Test (Shapiro-Wilk) (夏皮罗-威尔克正态性)”正态性检验结果显示P=0.063<0.1,提示数据不满足正态性条件。本案例宜选用配对样本Wilcoxon符号秩检验。
(一) 建立检验假设,确定检验水准
H0:差值的总体中位数,即两种方法所得结果无差别
H1:Md≠0,即两种方法所得结果有差别
a = 0.05
(二) 计算检验统计量
1. 计算差值
使用新法减去原法计算两组数据的差值,即图2中(4)=(3)-(2)。
2. 编秩
(1)将图2中第(4)列差值都取绝对值。
(2)以绝对值的大小从小到大编秩次(即编秩序号);若遇到差值为0的对子数应舍去,同时样本例数相应减少;若遇到绝对值相等的差值,则取平均秩次,又称同秩或结。
(3)让秩次保持原差值的正负号(即符号秩)。
(4)求秩和,正秩和(T+)为65,负秩和(T-)为13。
3. 计算T值
分别求出正负秩次之和T+和T-,任取正秩和或负秩和为T。本例T=13或65。

(三) 确定P值,作出推断结论
当n≤50时,查(T值界值表)。查表时,自左侧找到n,将检验统计量T值与相邻左侧一栏的界值相比,若T在上、下界值范围内,其P值大于表上方相应概率水平;若T值恰好等于界值,其P值等于(一般是近似等于)相应概率水平;若T值在上、下界值范围外,其P值小于相应概率水平,可向右移一栏,再与界值相比。
本例n=12,T=13或65,查(T值界值表),得双侧P=0.05。按α=0.05水准,拒绝H0,接受H1,差异有统计学意义,可认为两种方法所得结果有差别。