二分类logistic回归分析 (Binomial Logistic Regression Analysis)——MedCalc软件实现

关键词：MedCalc; 二分类logistic回归; 二项logistic回归; 二元logistic回归; 逻辑回归; EPV原则

一、案例介绍

探讨经皮内镜下腰椎间盘摘除术治疗腰椎间盘突出疗效不佳的主要影响因素，纳入经该手术治疗的患者424例，随访12个月观测治疗效果，预后不佳记录为“1”，预后良好记录为“0”；其余变量及编码为性别(0=女，1=男)、年龄(0=60岁以下，1=60岁及以上)、手术时间(min)、突出部位(1=单侧，2=中央，3=极外侧)、突出分类(1=膨出型，2=突出型，3=脱垂型)、Modic改变(1=I级，2=II级，3=III级)、是否钙化(0=未钙化，1=钙化)、矢状径(cm)、退变级别(1=I-III级，2=IV级，3=V级)。部分数据见图1。本案例数据可从“附件下载”处下载。

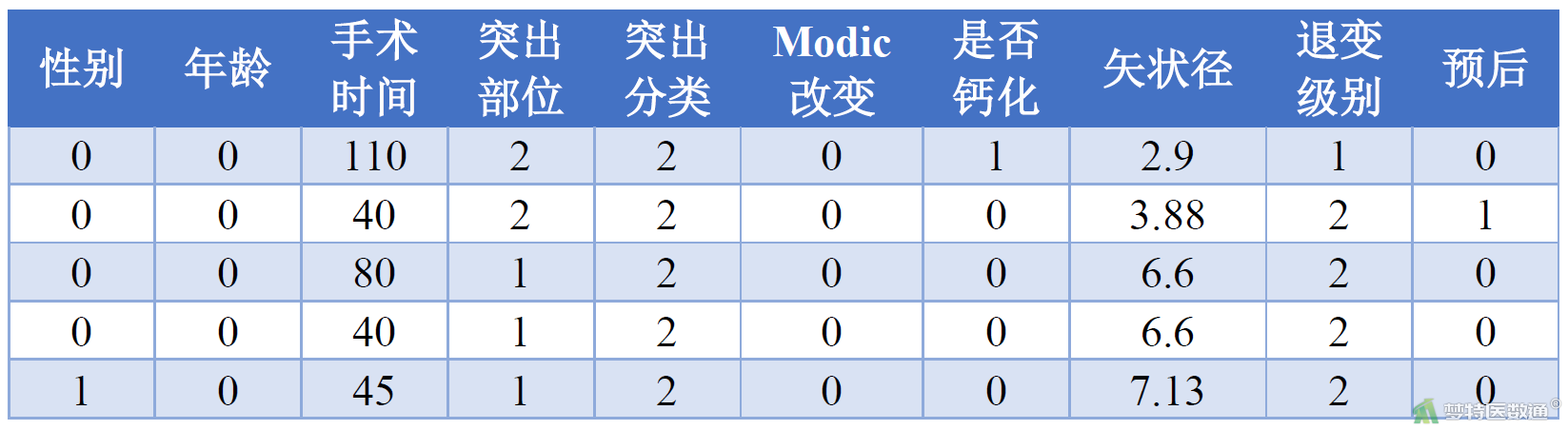
二、问题分析

本案例的分析目的是探讨经皮内镜下腰椎间盘摘除术治疗腰椎间盘突出疗效不佳的主要影响因素，由于因变量是二分类变量，因此可以使用二分类logistic回归分析。但需要满足7个条件：

条件1：因变量为二分类变量。本研究中因变量是治疗效果“不佳”和“良好”，为二分类变量，该条件满足。

条件2：至少有1个自变量。自变量可以是分类变量也可以是连续变量。本研究中有多个自变量，类型各异，该条件满足。

条件3：各观测行间相互独立。对研究设计和数据收集的过程进行分析，可判断本案例中观测值之间不存在互相影响的情况。

条件4：例数较少类的因变量例数为自变量个数的10~15倍(EPV原则)，且经验上两组的人数最好＞30例，参照水平组不应少于30或50例。该条件需要通过软件分析后判断。

条件5：自变量之间无多重共线性。该条件需要通过软件分析后判断。

条件6：自变量不存在显著的异常值。该条件需要通过软件分析后判断。

条件7：数据未出现完全分离或拟完全分离现象。该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一)数据准备

• 打开MedCalc软件，导入数据，见图2

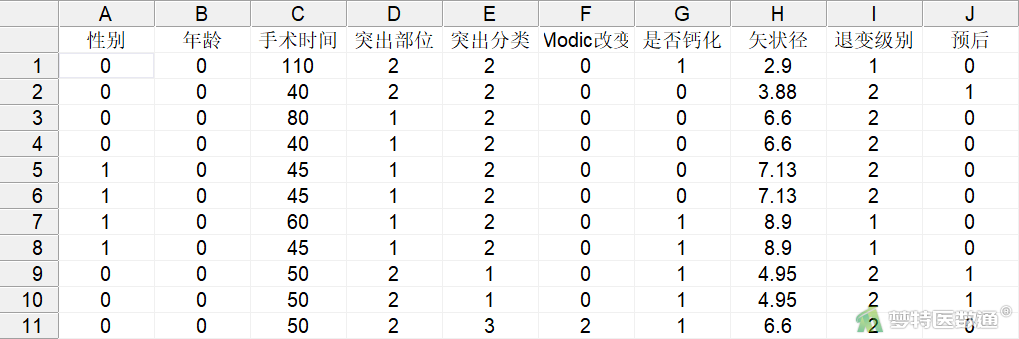
• 点击左侧“变量”，出现“变量”对话框，在此处选中需要进行标签设置的变量后点击右侧“属性”(图3)即可出现“变量属性”对话框。

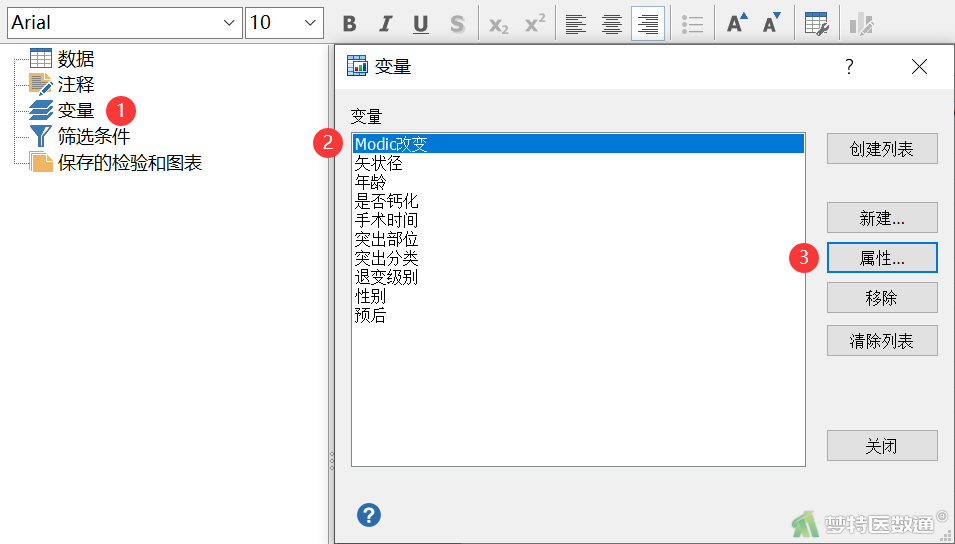
• 在“变量属性”对话框中设置变量的标签，以变量“Modic改变”为例，如图4所示。

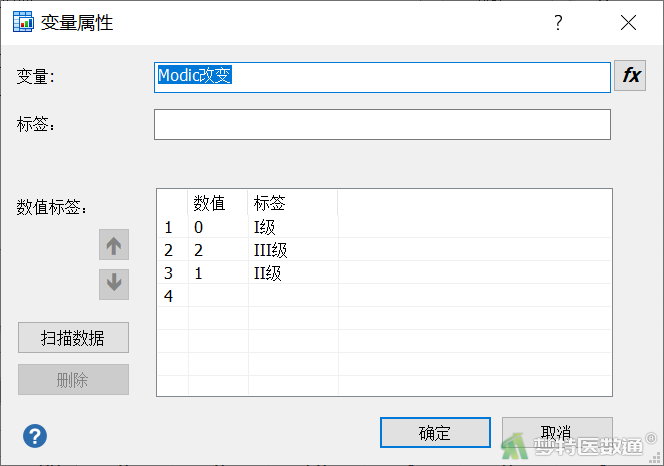
(二)适用条件判断

1. 条件4判断(因变量和自变量样本例数)

(1) 软件操作

• 选择“统计”—“交叉表”—“相对风险和机会比”(图5)。

• 在“相对风险和机会比”对话框中，“结果”中选择任一自变量“性别”，“组”中选择因变量“预后”，右侧“选项”部分勾选“机会比”，然后点击“确定”(图6)。即可得到因变量“预后”和自变量“性别”的例数、卡方检验结果和OR值。

• 要统计其他自变量的个数及进行卡方检验需重复以上两个步骤，并在“结果”中改选需要统计的自变量，其他不变，此处不一一描述(请读者自行操作)。

(2) 结果解读

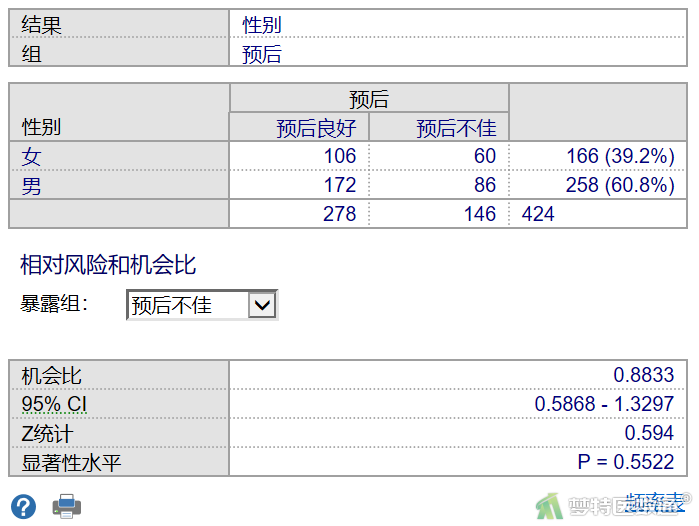
由图7可见，“预后”中“0”代表“预后良好”，总共为278例，“1”代表“预后不佳”，总共为146例。根据“例数较少类的因变量例数为自变量个数的10~15倍(EPV原则)”，本案例可纳入10~15个自变量进行多因素二分类logistic回归分析。

由图7可见，不同性别、不同预后的情况下，因变量的例数均大于30。变量“性别”计算的OR值(机会比)为0.8833，P值为0.5522>0.05，差异无统计学意义。OR值的解读需要结合卡方检验的显著性，一般情况下卡方检验显著时，OR值才有价值。

其他分类自变量的卡方检验步骤和结果此处不一一描述(请读者自行操作、查看)。从分析结果可知，只有当“突出部位”水平为“3”极外侧时、“突出分类”水平为“1”膨出型时、“退变级别”水平为“3”V级时，因变量例数小于30，所以当这些自变量在纳入多因素分析模型时，应注意避免例数较少的水平被选为参照组。

2. 条件5判断(多重共线性诊断)

多重共线性诊断是查看纳入多因素模型的变量间是否存在共线性，详见后文。

3. 条件6判断(异常值检测)

(1) 软件操作

• 选择“统计”—“异常值检测”(图8)。

• 以自变量“手术时间”的异常值检验为例：在“异常值检测”对话框的“变量”中选择变量“手术时间”，其他设置保持默认，见图9。其他自变量的异常值检测步骤和结果此处不一一描述(请读者自行操作、查看)。

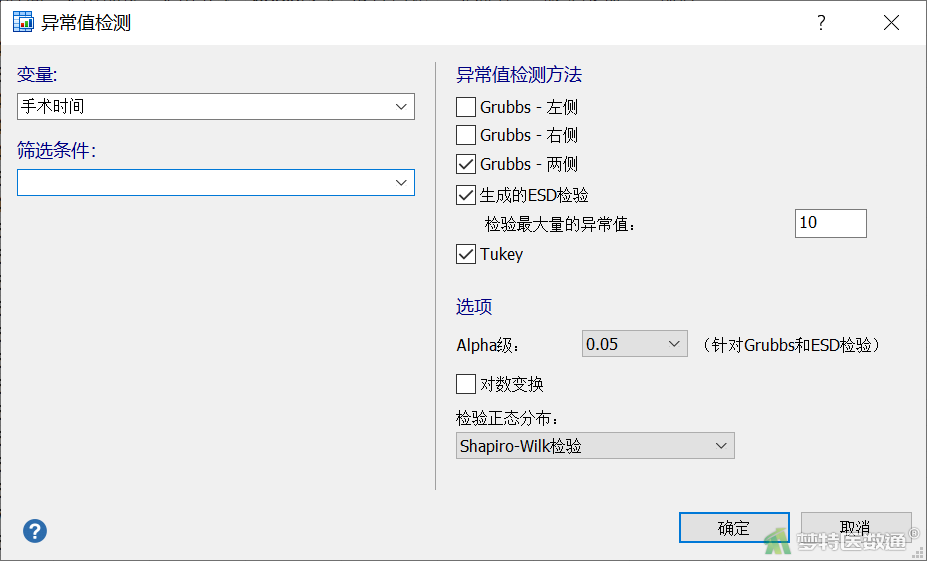
(2) 结果解读

图10为变量“手术时间”的异常值检验结果，尽管提示有一些异常值，但是根据专业可判断这些数值不是真正的异常值。

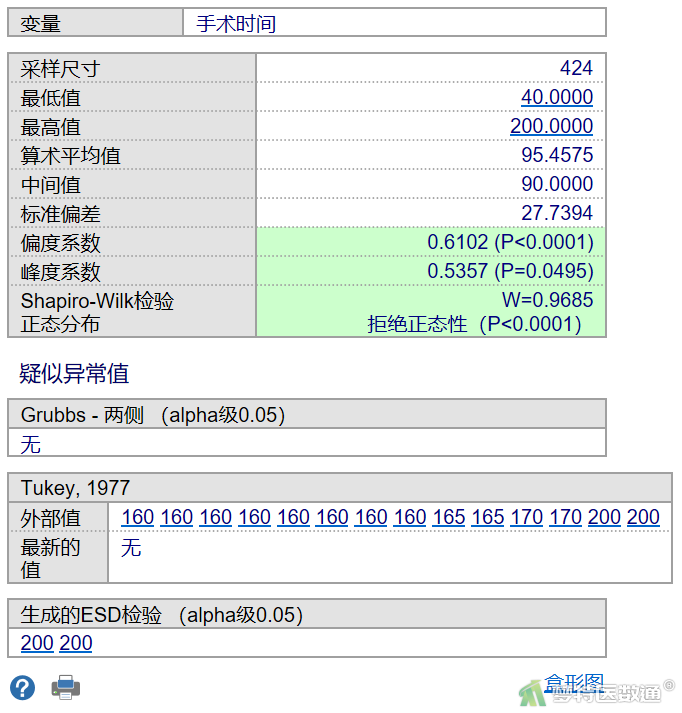
其他连续性自变量的的异常值检验操作同上，结果均显示未发现需要特殊处理的异常值。

4. 条件7判断(完全分离检测)

完全分离，指某一个自变量本身或者某几个自变量的线性组合，对因变量的预测结果与实际情况完全一致，常表现为OR值无穷大。通过以上分析可知，性别对应各变量例数均大于30，OR值为0.883，并非无穷大。其他自变量的卡方检验结果也显示不存在OR值无穷大的情况，所以该条件满足。

(三) 回归分析

1. 单因素分析

(1) 软件操作

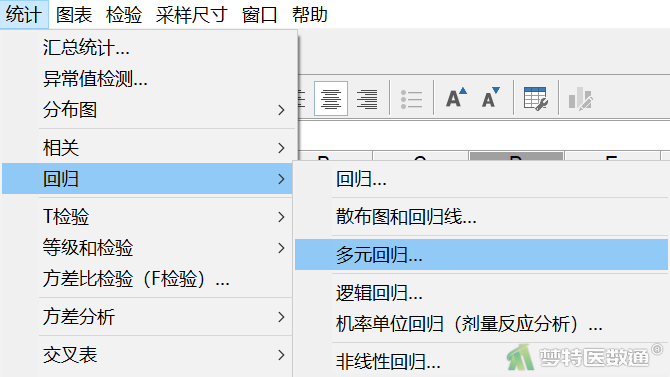
• 点击“统计”—“回归”—“逻辑回归”(图11)。

• 在“逻辑回归”对话框中将变量“预后”选入“因变量”，变量“性别”选入“独立变量”，然后点击“确定”(图12)，可得到变量“性别”的单因素分析结果。其他自变量的单因素分析步骤和结果此处不一一描述(请读者自行操作、查看)。

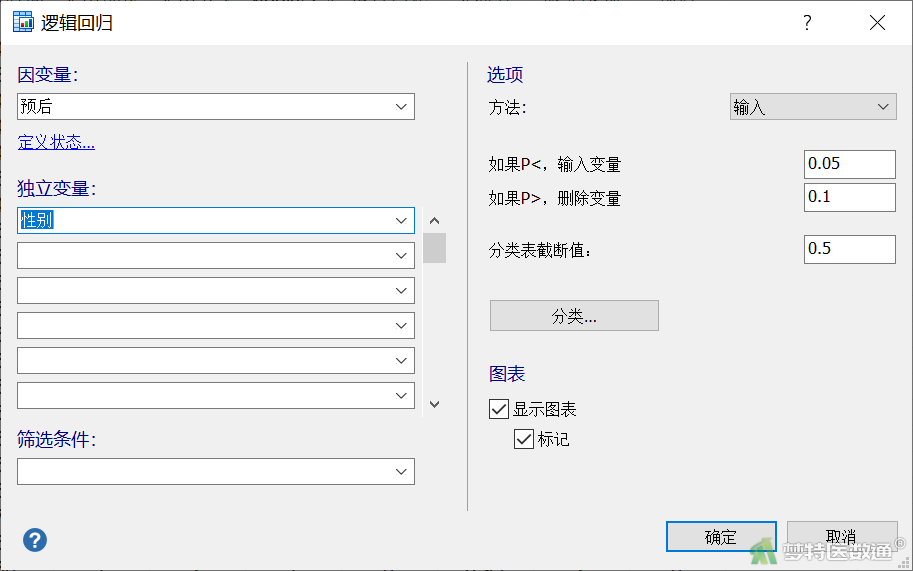
(2) 结果解读

• 单因素分析时，可将检验水准提高到0.1~0.2。图13显示了“性别”的单因素分析结果，P=0.553>0.1，差异无统计学意义，同时从专业角度判断性别对预后的影响不大，故考虑在多因素分析时不纳入该变量。

• 其他自变量的单因素分析结果显示，变量“年龄”、“手术时间”、“突出部位”、“是否钙化”、“矢状径”和“退变级别”的单因素分析P值小于0.1，可以纳入多因素分析模型。

2. 条件5判断(多重共线性诊断)

(1) 软件操作

• 点击“统计”—“回归”—“多元回归”(图14)。

• 在“多元回归”对话框中将变量“预后”选入“因变量”，单因素分析中有统计学意义的变量“年龄”、“手术时间”、“突出部位”、“是否钙化”、“矢状径”和“退变级别”选入“独立变量”。右侧“方法”部分选择“输入”，下方勾选“报告和方差膨胀因子(VIF)”。

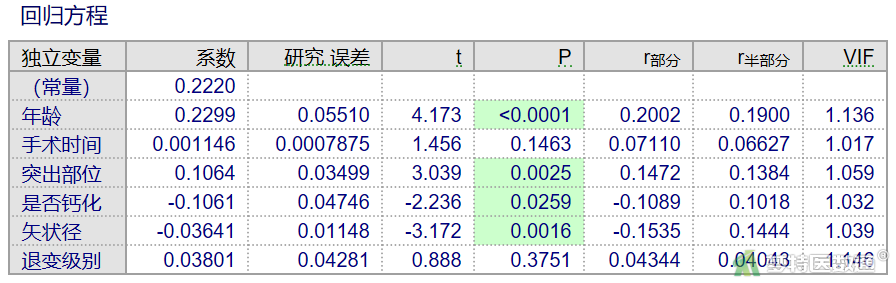
(2) 结果解读

如果“VIF(方差膨胀因子)”大于5，则提示有共线性存在。本例中VIF均小于5，提示自变量之间不存在多重共线性(图16)。如果数据存在多重共线性，需用复杂的方法进行处理，其中最简单的是剔除引起共线性的因素之一，剔除哪一个因素可以基于理论依据。

3. 多因素分析

(1) 软件操作

• 点击“统计”—“回归”—“逻辑回归”(图11)。
• 在“逻辑回归”对话框中将变量“预后”选入“因变量”，“年龄”、“手术时间”、“突出部位”、“是否钙化”、“矢状径”和“退变级别”选入“独立变量”。右侧“方法”部分可以选择“输入”、“向前”、“向后”或“逐步”，此处选择“输入”(图17)。

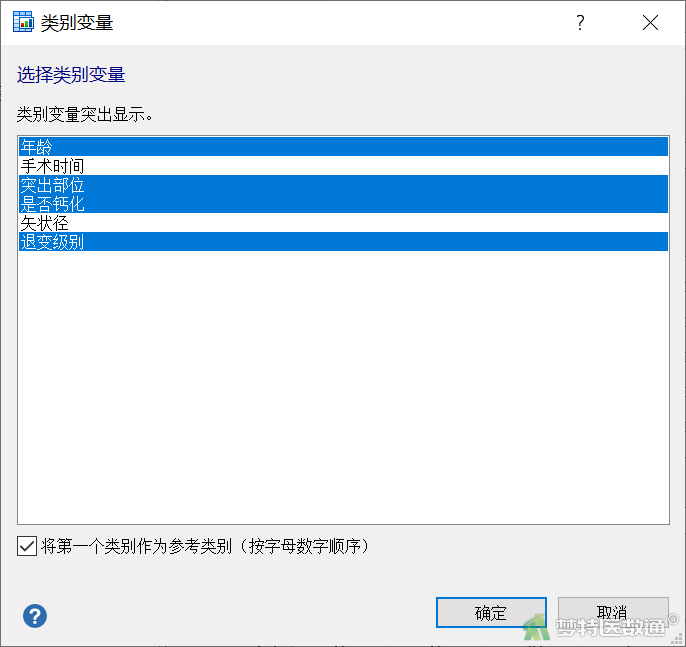
• 对于连续资料(如手术时间、矢状径)、二分类或有序分类资料(如年龄、退变级别)可以直接引入回归方程，不需要重新赋值。而对于无序分类资料(如突出部位)则应定义哑变量。点击“逻辑回归”对话框中的“分类”，出现图18所示的“类别变量”对话框，可定义自变量中的无序分类变量。点击变量名称，使之高亮，即可将变量设置为分类变量，再次点击，可取消设置。在MedCalc中默认以变量的第一个类别(按字母数字顺序)作为参考类别，若不勾选，则是以最大的分类作为参考分类。图18中已经默认选择了分类变量“年龄”、“突出部位”、“是否钙化”和“退变级别”，可以保持不变，然后点击“确定”回到“逻辑回归”对话框，最后点击“确定”得到多因素分析结果。

(2) 结果解读

图19是模型整体拟合优度检验结果，χ²=66.145，P<0.001，全模型有统计学意义，表明模型中的自变量有助于预测结局。

图20是对最终多因素模型中单一回归系数的假设检验，可以判断该变量对模型是否有影响。可见有统计学意义的变量为“年龄”“突出部位”“是否钙化”“矢状径”。

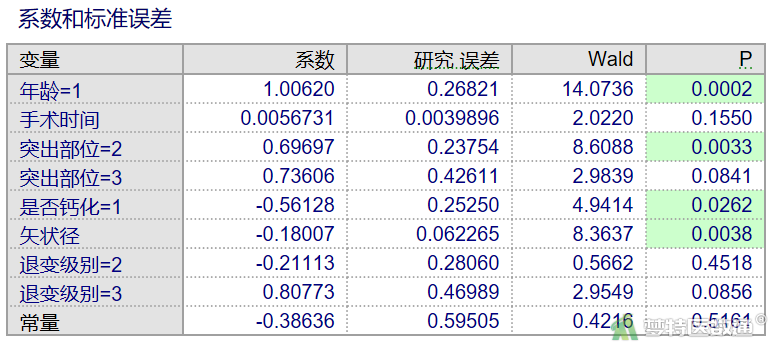
图21显示年龄的优势比OR=2.735，其95%CI为(1.617~4.627)，结合图21中“年龄”对应的系数，表明年龄60岁及以上术后效果不佳的风险约是年龄小于60岁的2.735倍。由于以“突出部位=1”为参考分类，“突出部位=2”与“突出部位=1”比，OR=2.008，其95%CI为(1.260~3.198)。是否钙化的优势比OR=0.571，其95%CI为(0.348~0.936)，表明钙化患者术后不佳的风险相比非钙化患者约降低42.9%。矢状径的优势比OR=0.835，其95%CI为(0.739~0.944)，表明矢状径每增加1 cm，术后效果不佳的风险约降低16.5%。

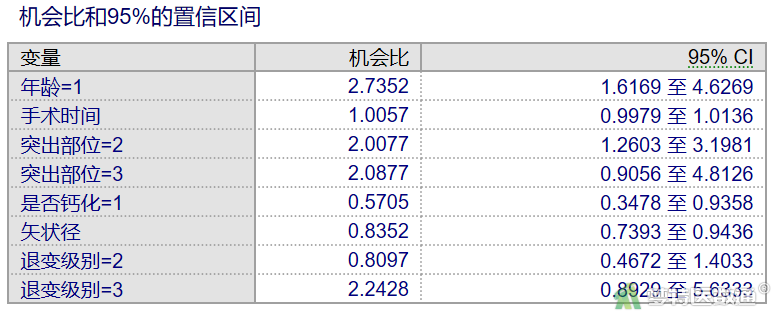
图22分类表用于评价logistic回归模型的预测准确性，本例的预测准确率为71.70%，提示该模型的判断效果一般。

图23为ROC曲线分析，是评价logistic回归模型的另一种方法。本例ROC曲线下面积(AUC)为0.735，95%CI为0.690~0.776，提示该模型的判断效果一般。

四、结论

本研究采用二分类Logistic回归探讨经皮内镜下腰椎间盘摘除术治疗腰椎间盘突出疗效不佳的主要影响因素。因变量例数分布满足样本量需求，变量之间不存在严重共线性和异常值，数据不存在完全分离现象。

9个自变量经过分析后，最终有6个变量(年龄、手术时间、突出部位、是否钙化、矢状径和退变级别)进入多模型，其中年龄60岁及以上的患者术后不佳的风险约是60岁以下患者的2.735倍(95%CI：1.617~4.627；P<0.001)；突出部位为“中央”的患者术后效果不佳的风险分别约为“单侧”患者的2.008倍(95%CI：1.260~3.198；P=0.003)；矢状径每增加1 cm，术后效果不佳的风险约降低16.5% (OR=0.835，95%CI：0.739~0.944；P=0.004)；钙化患者术后不佳的风险相比非钙化患者约降低42.9%(OR=0.571，95%CI：0.348~0.936；P=0.026)。所建立的模型有统计学意义(χ²=66.145，P<0.001)，模型预测准确率为71.70%，ROC曲线下面积为0.735(95%CI：0.690~0.776)，该模型的判断效果一般。

五、分析小技巧

• 自变量进入模型的形式

无序多分类自变量需要以哑变量形式进入模型，在MedCalc中默认以第一类别(按字母数字顺序)作为参考类别，但需要注意以下事项：①参照水平要具有实际意义，否则会失去比较的目标，如“其他”一般不适宜做参照水平。②参照水平应有一定的例数(不低于30或50例)，否则将导致与其比较的其他组的置信区间较大。③哑变量整体分析无统计学意义时，所有哑变量都不用再纳入模型；整体分析有统计学意义时，尽管有些哑变量无统计学意义，但仍需要纳入模型，即“同进同出”原则。

有序多分类自变量进入模型有多种方式备选，但应选择最具合理性的方式：①直接以计量资料形式带入模型：此时得到的模型较为简洁，也容易解释。但应用的前提是自变量的每个水平对因变量的影响作用基本一致，可通过观察哑变量各水平的回归系数值是否存在等级变化关系进行判定。建议先将有序多分类资料分别以哑变量和连续变量的形式引入模型，观察每个哑变量的回归系数间是否存在等级关系，并对两个模型进行似然比检验，如果似然比检验无统计学意义，且每个哑变量的回归系数间存在等级关系，则可以将该自变量以连续变量形式引入模型，否则还是采用哑变量的方式引入模型。②设置哑变量：参照无序多分类资料。③当有序多分类变量的等级水平与因变量结局不成线性关系时，应采用最优尺度回归探讨效应拐点。

定量资料进入模型有多种方式备选，但也应选择最具合理性的方式：如果某计量资料能以计量形式进入模型(有统计学意义)，那么转化后应当同样能进入模型，且OR值会显著增加。①直接带入模型，尽管此种方法较为简单，但仍不做首选推荐。因为此时得出的OR值一般较小，即自变量变化一个单位对结局风险的影响其实是有限的，不能贴近专业解释。 如果资料分布严重失衡时(非均匀分布)尤其不能直接带入模型。但以计量资料形式直接进入模型往往模型的拟合效果较好。②根据专业意义降维后(如根据BMI指数分级标准降维为有序多分类资料)，参照有序多分类资料或者二分类资料处理方式。③如果没有专业划分标准，可以资料分布形式根据四分位数间距或等分法降维或者标准化后按Per 1 sd (每一个标准差)降维。④建立自变量和因变量之间的ROC曲线，根据约登指数进行二分类降维。⑤中位数(非正态分布)或者均数(近似正态或正态分布)降维。⑥当自变量的单位不合适导致因变量的风险改变很小时，可对自变量采取缩小(如除以100)或扩大(如乘以10)相应倍数的方式。

• 自变量进入模型的形式

关于自变量是否纳入多因素分析模型除了根据本章节介绍的判定方法以外，还可采取以下策略：

专业原则：首先需要考虑的就是专业原则，这一点最为重要。如果目前专业知识有证据表明该变量与结局发生有关，那么不论该变量单因素分析结果是否有统计学意义，都应纳入多因素分析模型。

以单因素分析为基础：当分析的变量较多时，可先采取单因素分析方法，对有统计学意义的变量再纳入多因素分析。此时单因素分析检验水准可设置为0.1—0.2，如果样本量较大，可将检验水准设置为较为严格；如果样本量较小可将检验水准设置较为宽松。

比较原则：可以尝试多种方法对该变量进行分析，如采用多种自变量进入方法分析，或将计量资料降维后再分析，如果变量在多种进入方法和不同变量类型时，均能在多因素分析模型中有统计学意义，则表明该变量的确是因变量的真正影响因素。