一般情况下,当因变量是连续性变量时,我们常使用线性回归分析若干自变量与因变量的关联;而当因变量是分类(二分类、无序多分类和有序多分类)变量时,我们常考虑使用logistic回归(logistic regression)进行分析。目前,logistic回归在流行病学、实验研究、临床试验评价及疾病的预后因素分析等方面均有广泛应用。logistic回归属于概率型非线性回归,除了用于影响因素分析,预测和判别也是logistic回归模型的一个重要应用。
根据因变量的不同,可将logistic回归分为二分类logistic回归(binary logistic regression)、无序多分类logistic回归(multinomial logistic regression)和有序多分类logistic回归(ordinal logistic regression);根据是否采用匹配设计,又可将二分类logistic回归分为非条件logistic回归(unconditional logistic regression)和条件logistic回归(conditional logistic regression)。本篇文章将举例介绍非条件二分类logistic回归的假设检验理论。
关键词:二分类logistic回归; 二项logistic回归; 二元logistic回归; 逻辑回归; EPV原则
一、基本概念
(一) 二分类logistic回归模型
二分类logistic回归模型的因变量Y 是二分类变量,其取值常编码为0和1。
\(\mathrm{Y}=\left\{\begin{array}{l} 1 \text { (有效、发病、名年等) } \\ 0 \text { (无效、末发病、存活等) }\end{array}\right.\)
其中1代表阳性结果,0代表阴性结果。假设影响Y取值的(可能)影响因素有m个,即X1、X2、X3、…、Xm。此时,Y=1的概率记为π,Y=0的概率为1-π。由于概率π的取值范围为[0,1],影响因素X1~Xm线性组合\(\left(\beta_{0}+\beta_{1} X_{1}+\beta_{2}X_{2}+\beta_{3} X_{3}+\cdots+\beta_{m}X_{m}\right)\)的取值范围为(-∞,+∞)。因此,若要建立概率π与影响因素线性组合的等式关系(回归关系),需要对π进行logit变换,即\(\operatorname{logit}(\pi)=\ln\left(\frac{\pi}{1-\pi}\right)\)其取值范围为(-∞,+∞)。所建立的方程如下:
\(\operatorname{logit}(\pi)=\ln\left(\frac{\pi}{1-\pi}\right)=\beta_{0}+\beta_{1}X_{1}+\beta_{2} X_{2}+\beta_{3}X_{3}+\cdots+\beta_{m} X_{m}\)
经过简单变换,可以转换为:
\(\pi=\frac{e^{\beta_{0}+\beta_{1} X_{1}+\beta_{2}X_{2}+\beta_{3} X_{3}+\cdots+\beta_{m}X_{m}}}{1+e^{\beta_{0}+\beta_{1} X_{1}+\beta_{2}X_{2}+\beta_{3} X_{3}+\cdots+\beta_{m} X_{m}}}\)
在流行病学中,我们把阳性结果和阴性结果的概率之比称为优势(odds),即\(\frac{\pi}{1-\pi}\),因此方程式还可以变换为:
\(\ln (\text { odds })=\operatorname{logit}(\pi)=\beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}+\beta_{3}X_{3}+\cdots+\beta_{m} X_{m}\)
\(\text { odds }=e^{\beta_{0}+\beta_{1}X_{1}+\beta_{2} X_{2}+\beta_{3}X_{3}+\cdots+\beta_{m} X_{m}}\)
在上述的4个方程式中,β0为常数项,β1、β2、β3、…、βm是对应影响因素(自变量)的回归系数。
(二) 回归系数的意义
类似于多重线性回归的解释,我们将logit (π)视为一个整体,回归系数βi的解释为:保持其他自变量不变,自变量Xi每改变一个单位,logit (π)的平均改变量。另外,我们可以通过第4个公式将回归系数与流行病学中的优势比/比值比(odds ratio, \(O R=\frac{o d d s_{1}}{o d d s_{0}}=\exp\left[\beta_{i}\left(s_{1}-s_{0}\right)\right]\))联系起来。OR可以反映病因研究中暴露与结局的关联强度。当β=0时,OR=1, 暴露与结局间不存在关联;当β≠0时,OR≠1,暴露与结局间存在关联。特殊地,如果Xi赋值为
\(X_{i}=\left\{\begin{array}{ll}1 & \text { (暴露) } \\0 & \text { (非暴露) }\end{array}\right.\)
则暴露组与非暴露组发病的优势比为
\(O R_{i}=\exp \left(\beta_{i}\right)\)
当自变量Xi的回归系数βi>0时,ORi>1,提示Xi是结局的危险因素;当βi<0时,ORi <1,提示Xi为保护因素。
二、适用条件
二分类logistic回归需要满足以下6个条件:
条件1:因变量为二分类变量。
条件2:至少有1 个自变量,可以是分类变量,也可以是连续变量。
条件3:因变量的观察结果相互独立。
条件4:例数较少类的因变量例数为自变量个数的10~15 倍(EPV原则),且经验上两组的人数最好>30例,自变量的参照水平组不应少于30或50例。
条件5:自变量之间无多重共线性。
条件6:自变量不存在明显的异常值。
三、参数估计
(一) 回归系数估计
在使用实际数据进行分析时,通常采用极大似然估计(maximum likelihood estimate, MLE)对回归系数βi进行估计。对应的样本联合概率,即似然函数为:
\(L=\prod_{i=1}^{n}\pi_{i}^{Y_{i}}\left(1-\pi_{i}\right)^{1-Y_{i}}\)
式中L为似然函数,∏为连乘符号,πi表示第i例研究对象在相应暴露情况下发生阳性结果的概率。如果实际出现的是阳性结果,Yi=1,否则Yi=0。
根据最大似然原理,在一次抽样中获得现有样本的概率应该达到最大,即似然函数L 应该达到最大值。为了简化计算,通常取似然函数的对数形式,即
\(\ln L=\sum_{i=1}^{n}\left[Y_{i} \ln\pi_{i}+\left(1-Y_{i}\right)\ln \left(1-\pi_{i}\right)\right]\)
可使用Newton-Raphson迭代方法得出常数项β0和回归系数β1、β2、…、βm的估计值及其标准误。
(二) OR值的估计
\(\widehat{O R}_{l}=\exp\left[\beta_{i}\left(s_{1}-s_{0}\right)\right]\),当样本量较大时,βi的抽样分布近似服从正态分布,则ORi的1-α置信区间为
\(\left(e^{\beta_{i}-Z_{\alpha / 2} S_{\beta_{i}}},e^{\beta_{i}+Z_{\alpha / 2} S_{\beta_{i}}}\right)\)
式中的\(S_{\beta_{i}}\)为βi的标准误。
四、假设检验
建立由样本估计参数的logistic回归模型后,需要对拟合的logistic回归模型进行假设检验,判断总体回归模型是否成立或是自变量的回归系数否有统计学意义。假设检验包括:logistic回归模型的检验和logistic回归系数的检验。
(一) 回归模型检验
检验模型中所有自变量的线性组合\(\left(\beta_{0}+\beta_{1} X_{1}+\beta_{2}X_{2}+\beta_{3} X_{3}+\cdots+\beta_{m}X_{m}\right)\)是否与logit(π)或所研究事件的对数优势比ln(odds)存在线性关系。检验的方法有似然比检验(likelihood ratio test)、计分检验(score test)和Wald检验(Wald test)等。这里介绍常用的似然比检验。
似然比检验的基本思想是比较在两种不同假设条件下的对数似然函数值,看两者的差别大小。先拟合一个不包含待检验变量在内的logistic回归模型,求其对数似然函数值lnL0;然后把需要检验的变量加入该模型得到一个新的对数似然函数值lnL1,检验统计量为:
G=2(lnL1-lnL0)
当样本含量较大时,在零假设下得到的G统计量近似服从自由度为d(d=p-l)的χ2分布。p和l分别为前后两个模型包含的自变量个数。
(二) 回归系数检验
对每个自变量的回归系数进行检验,即判断每个自变量对模型是否有贡献。常用的假设检验为Wald检验。
Wald检验只需将各参数βi的估计值bi与0比较,并用它的标准误\(S_{b_{i}}\)作为参照;为检验H0:βi=0,H1:βi≠0,计算如下统计量
\(u=\frac{b_{i}}{S_{b_{i}}}\)
或
\(\chi^{2}=\left(\frac{b_{i}}{S_{b_{i}}}\right)^{2}\)
当样本含量较大时,在零假设下得到的u统计量近似服从标准正态分;而χ2值近似服从自由度为1的χ2分布。
五、案例分析
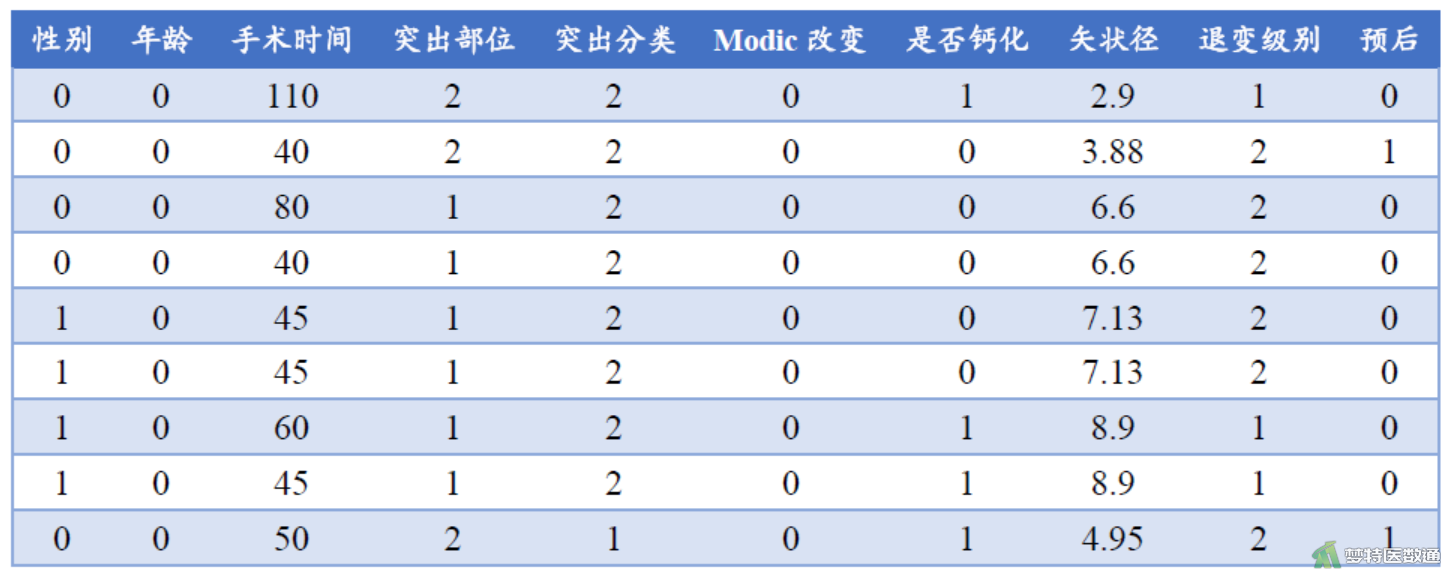
探讨经皮内镜下腰椎间盘摘除术治疗腰椎间盘突出疗效不佳的主要影响因素,纳入146例治疗效果“不佳”(记录为1)的患者,278例治疗效果“良好"(记录为0)的患者,并收集其余变量信息。其余变量及编码为性别(0= 女,1= 男)、年龄(0=60 岁以下,1=60 岁及以上)、手术时间(min)、突出部位(1= 单侧,2= 中央,3= 极外侧)、突出分类(1= 膨出型,2= 突出型,3= 脱垂型)、Modic 改变(1=Ⅰ级,2=Ⅱ级,3=Ⅲ级)、是否钙化(0= 未钙化,1= 钙化)、矢状径(cm)、退变级别(1=Ⅰ-Ⅲ级,2= Ⅳ级,3=Ⅴ级)。部分数据见图1 。
六、案例分析
对于本案例数据,连续性自变量加上分类变量的哑变量,共有13个自变量,建立的检验假设步骤如下:
(一) 回归模型检验
1. 建立假设检验,确定检验水准
H0:β1=β2=、…、=β13=0
H1:βi (i=1、2、…、13)不全为0
α=0.05
2. 计算检验统计量
似然比检验统计量G=2(lnL1-lnL0)。式中L1为包含性别、年龄、手术时间等13个自变量的似然函数, L0为仅包含常数项的似然函数。
通过软件可计算得到统计量G=68.285。
3. 确定P值,做出统计推断
统计量G服从自由度为13(连续性自变量个数+分类变量哑变量个数)的χ2分布。由此可确定,P<0.001,即模型有统计学意义,表明模型中至少存在一个自变量具有统计学意义。
(二) 回归系数检验
对每个自变量的回归系数进行检验,即判断每个自变量对模型是否有贡献。常用的假设检验为Wald检验。
1. 建立假设检验,确定检验水准
H0:βi=0
H1:βi≠0
α=0.05
2. 计算检验统计量
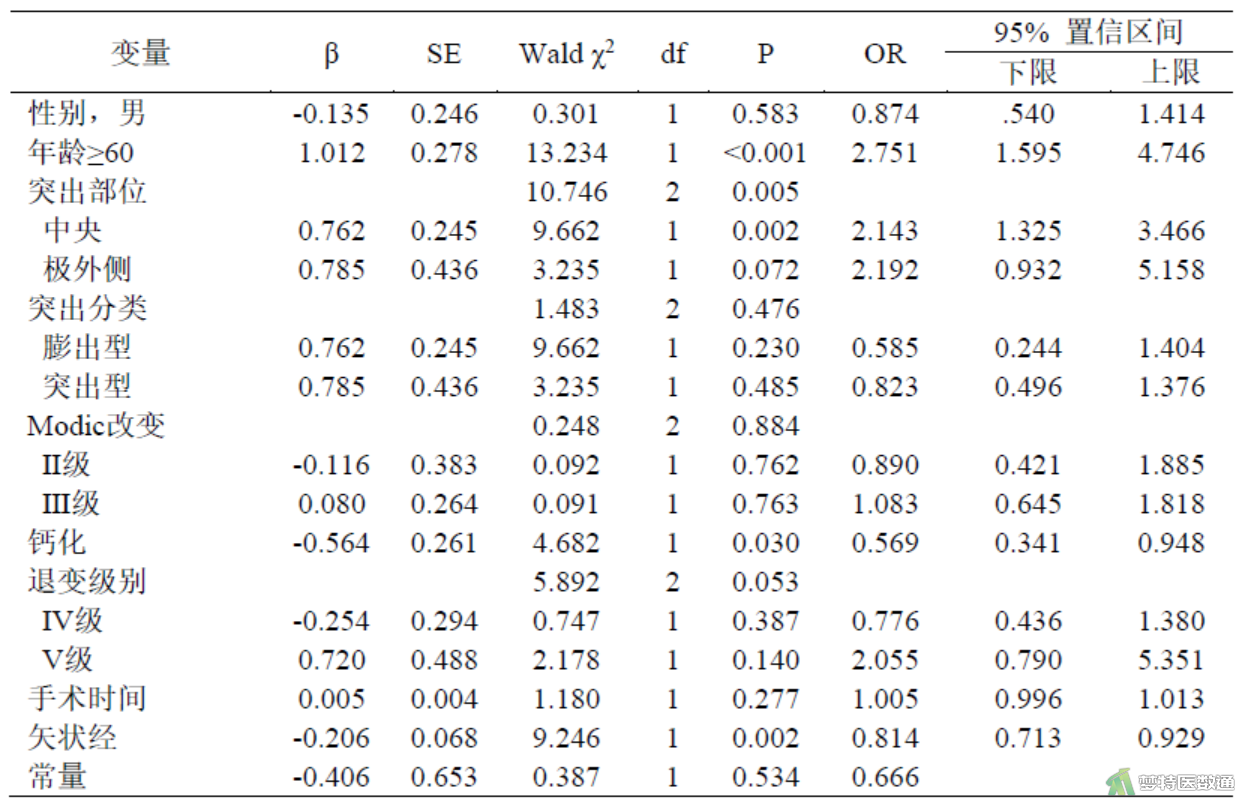
Wald检验的统计量Wald χ2服从自由度为1的χ2分布,Wald χ2详见图2。
3. 确定P值,做出统计推断
根据Wald χ2值,可确定对应的P值,见图2。可知,年龄(P<0.001)、突出部位(P=0.005)、钙化(P=0.030)和矢状经(P=0.002)在模型中有统计学意义,是预后的影响因素。其中年龄60岁及以上的患者术后不佳的风险是60岁以下患者的2.751倍(95%CI:1.595~4.746;P<0.001);突出部位为“中央”的患者术后效果不佳的风险是“单侧”患者的2.143倍(95%CI:1.325~3.466;P=0.002);“钙化”患者术后不佳的风险比“非钙化”患者低43.1%(OR=0.569,95%CI:0.341~0.948;P=0.030);矢状径每增加1 cm,术后效果不佳的风险降低18.6% (OR=0.814,95%CI:0.713~0.929;P=0.002);