在前面文章介绍了Probit回归的相关理论(Probit回归的理论介绍),已知Probit回归可用于计算半数致死剂量(LD50)、半数有效剂量(ED50)等剂量反应关系指标。本文将实例演示在MedCalc软件中基于原始数据的Probit回归计算LD50的操作步骤。
关键词:MedCalc; Probit回归; 概率单位回归; 半数致死量; LD50; 半数有效剂量; ED50
一、案例数据介绍
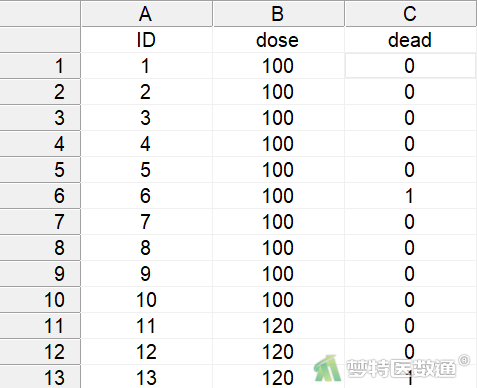
为研究某化学物质对小鼠的急性毒性大小,测试了不同剂量组的死亡情况,求该化学物质的LD50。ID为小鼠编号;dose为该化学物质剂量,包括100、120、140、160、180、200 mg/kg 6个剂量组;dead为小鼠死亡情况,0为存活,1为死亡。部分数据见图1。本案例数据可从“附件下载”处下载。
二、软件操作
选择“统计”—“回归”—“机率单位回归(剂量反应分析)”(图2)。

打开“机率单位回归(剂量反应分析)”对话框(图3),在“数据类型”下选择“二进制数据”,即原始数据类型;“剂量变量”中选入“dose”;“反应数量(应为‘反应变量’)”中选入“dead”;“选项”中勾选“剂量反应图”和“标记”。
三、结果解读
图4的“整体模型适配度(整体模型拟合优度检验)”显示,χ2 = -2ln(L0) - [-2ln(L)] = 78.859 - 48.625 = 30.234,P < 0.0001,即全模型有统计学意义。表示化学物质剂量与Probit(P)之间存在线性关系。
Cox & Snell \(R^2\) (\(R^2_{CS} \))与Nagelkerke \(R^2\) (\(R^2_{N} \))为伪\(R^2\),属于广义决定系数,是模型拟合优度的一种综合性指标。\(R^2_{CS} \)值越大说明模型拟合越好,但\(R^2_{CS} \)不能达到最大值1,只能在样本中基线概率为0.5时,能达到最大值0.75。\(R^2_{N} \)是\(R^2_{N} \)的调整值,最大可达到1。

“系数和标准误差”结果(图5)可知,浓度的确对死亡率有影响(P<0.001)。可得到概率单位回归方程:
Probit(P) = -4.57476 + 0.034264×dose
根据上述方程可计算死亡的预测概率,如剂量130 mg/kg时,
Probit(P) = -4.57476 + 0.034264×130 = -0.12044
在excel空白单元格中输入函数“=NORMSDIST(-0.12044)”,然后回车即可计算死亡预测概率为0.452067303,即45.2067303%。

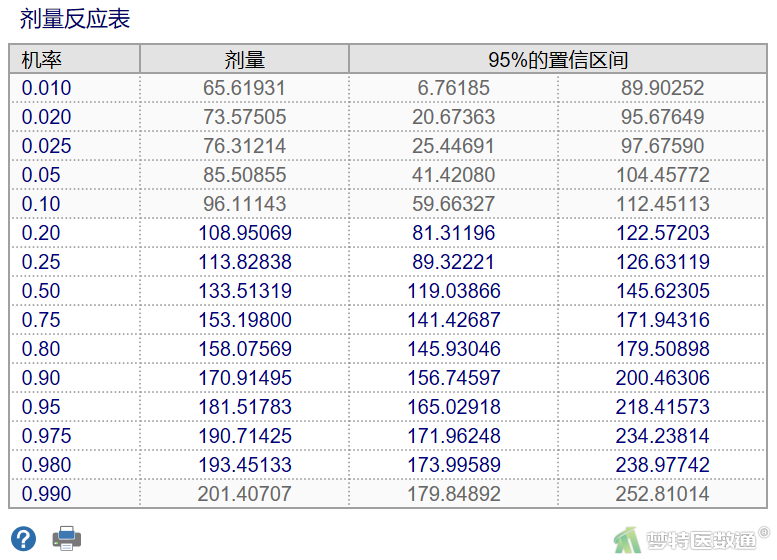
“剂量反应表”结果(图6)显示,LD50为133.51319 mg/kg,95%CI为(119.03866~145.62305) mg/kg,即给予该剂量水平时,将有50%的小鼠死亡。
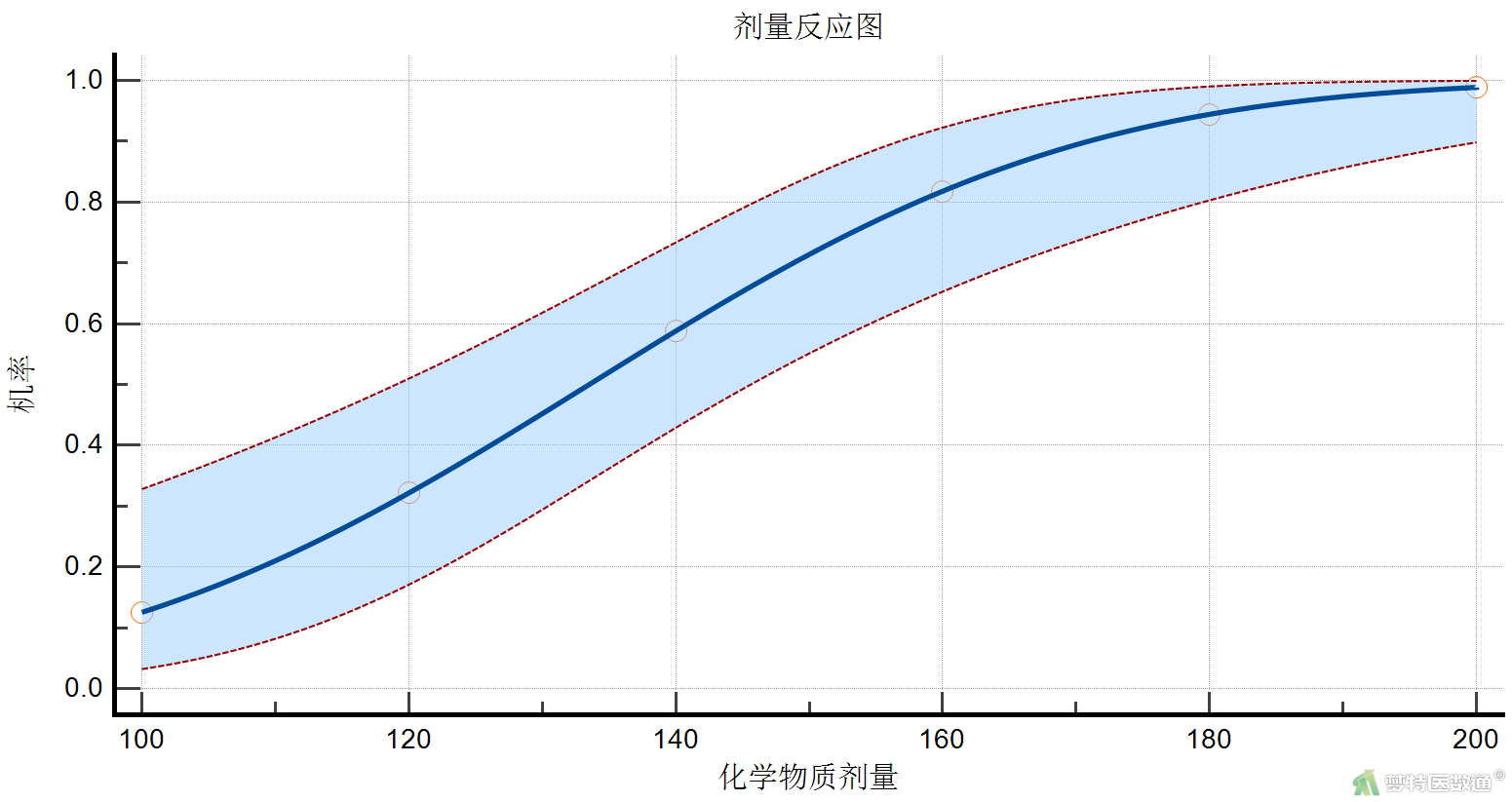
化学物质剂量与死亡概率的剂量反应关系图(图7)表明,剂量越大,死亡概率越高。
四、结论
通过Probit回归计算得到该化学物质对小鼠的LD50为133.51319 (95%CI为119.03866~145.62305) mg/kg。
五、知识小贴士
- “转换”主要用于是否对自变量进行对数变换以及转换的方式(常用对数及自然对数),在Probit分析时,要求协变量与Probit值呈直线关系,因此转换的最主要目的也在于此。如果协变量原始数据与Probit值之间呈大致直线关系,可无需对数据进行转换,否则需要进行相应方式的转换。若无法找到合适的转换方法达到直线趋势的效果,则不宜使用Probit回归进行数据分析。如果计量变量包含0,选择该选项时,MedCalc将自动加上一个很小的数值,使对数变换成为可能,并在结果的逆变换时减去该数值。
- “选项”中,“标记”用于标识数据,当选择“对数变换”以及剂量变量包含0时,选择此项将无效。