汇总资料的2×2卡方检验(2×2 χ² Test)——MedCalc软件实现

关键词：MedCalc; 卡方检验; 理论频数; 实际频数; 四格表

一、案例介绍

某中医院欲比较某经典名方控制高血压的效果。将200例高血压患者随机分到试验组和对照组，随访3个月后患者的血压控制情况。其中试验组中有效99例、无效5例，对照组中有效75例、无效21例。问该经典名方控制血压的效果如何？

两独立样本原始资料的卡方检验的数据录入可分为两种：第一种为频数资料，需要设置分组变量和频数变量；第二种为非频数资料(原始资料)，有观察变量和分组变量两列，每一行为一个患者的数据，该形式是在MedCalc软件中进行各种统计分析最常用的资料形式。本案例的数据采用了第1种录入方式。

二、问题分析

本案例的分析目的是探究某经典名方控制血压的效果，即比较试验组与对照组血压控制率是否有差异，针对这种情况可以制作四格表，并进行2×2 χ²检验。但需要满足3个条件。

条件1：分组变量与观察变量均为二分类变量。本案例的分组变量和观察变量均为二分类变量，该条件满足。

条件2：观察变量相互独立。本研究中各研究对象的观察变量都是独立的，不存在相互干扰的情况，该条件满足。

条件3：总例数≥40，且所有期望频数(理论频数)≥5。该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 适用条件判断

对于本案例数据，条件1和条件2均满足。但需要通过总例数和期望频数来选择具体的分析方法(Pearson χ²检验、连续校正χ²检验或Fisher确切概率法)。这一判断过程通过统计描述来完成，详见下文。

(二) 统计描述及推断

1. 软件操作

(1) 选择“检验”—“卡方检验”(图1)

(2) 打开“卡方检验”页面，在M1列和M2列依次输入试验组和对照组血压控制情况，点击“检验”，可得到分析结果(图2)。

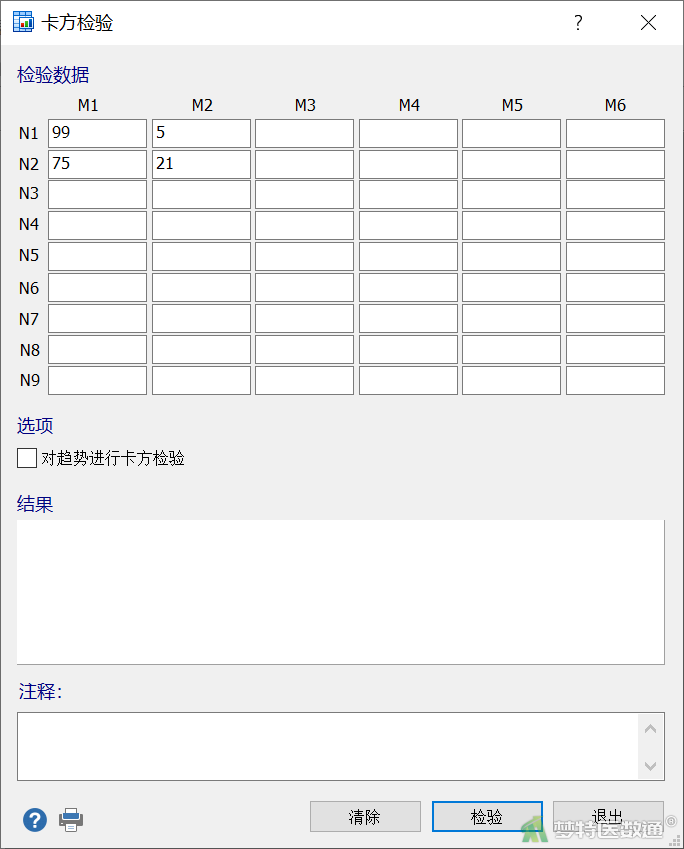
2. 结果解读

(1) 统计描述

MedCalc不能直接提供期望频数的结果，此处可用以下公式计算各个格子的期望频数。

\(T_{R C}=\frac{n_{R} n_{c}}{n}\)

可计算四个格子的理论频数分别为90.480、83.520、13.520和12.480，最小值均>5；且总例数为200例>40例，所以可以采用Pearson卡方检验的分析结果。

(2) 统计推断

图3的“结果”表格中提供了统计推断后的“卡方值”“DF(自由度)”“显著性水平(P值)”“列联系数”。

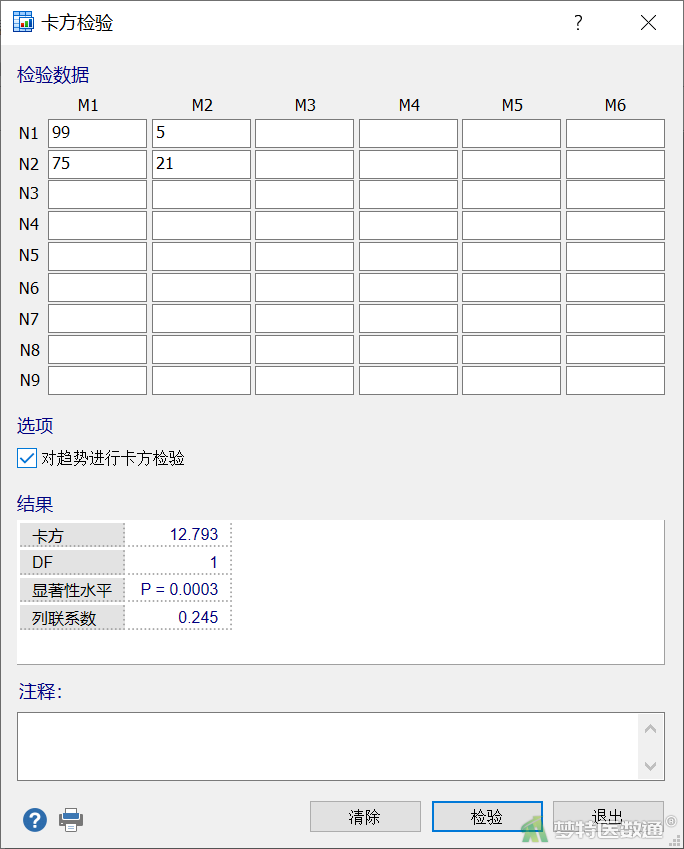
可知χ²=12.793，P=0.0003，按α=0.05水准，可认为差异有统计学意义，即试验组的血压控制率高于对照组。

四、结论

本研究采用2×2 χ²检验(独立样本χ²检验)比较两组高血压患者血压控制率有无差异。数据满足2×2 χ²检验的条件，总例数为200例，期望频数均＞5，采用Pearson χ²检验结果。

结果显示，χ²=12.793，P=0.0003，差异有统计学意义，试验组的血压控制率高于对照组。

五、知识小贴士

• 当总例数≥40，且所有期望频数(理论频数)≥5时，可使用Pearson χ²检验。当总例数≥40，有1个期望频数≥1且<5，可使用连续校正χ²检验(MedCalc不能提供校正卡方分析结果)。当总例数＜40或有1个期望频数＜1，需要使用Fisher确切概率法。
• 无论总例数的大小及期望频数分布情况如何，Fisher确切概率法均可使用。在计算机能够满足运行负荷的情况下，推荐使用确切概率法。如果使用Pearson χ²检验或连续校正χ²检验得出的P值比较接近检验水准，建议采用Fisher确切概率法。
• 关于χ²检验的更多内容详见χ²检验的注意事项——使用技巧。