在前面文章中介绍了负二项回归分析(Negative binomial regression analysis)的假设检验理论,本篇文章将实例演示在R软件中实现负二项回归分析的操作步骤。
关键词:R语言; R软件; 负二项回归; 过离散; overdisp
一、案例介绍
某市抽样调查了146名学生某一学年的缺课天数(Days),同时收集了他们的民族(Race;1=汉族,2=少数民族)、性别(Sex:1=男,2=女)、年龄(Age:1=10-12岁,2=8-10岁,3=6-8岁,4=小于6岁)和学习状况(Study:1=良好,2=一般)等信息,拟探究上述因素对学生缺课天数的影响。部分数据见图1。本文案例可从“附件下载”处下载。
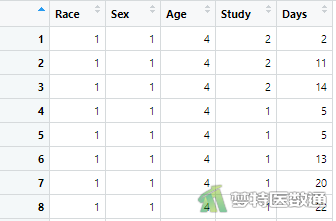
二、问题分析
本案例的分析目的是研究民族、性别、年龄、学习状况等对学生年缺课天数的影响。因变量为计数资料,服从Poisson分布或负二项分布,可以尝试使用负二项回归分析。但需要满足5个条件:
条件1:因变量为计数变量。本案例的因变量为年缺课天数,为计数变量,满足条件。
条件2:至少有1 个自变量,可以是分类变量,也可以是连续变量。本案例有民族、年龄、性别、学习状况共4个自变量,满足该条件。
条件3:各观测行间是非独立的,事件的发生有空间聚集现象;或因变量存在过离散现象,即方差远大于均数。由研究设计可知,学生缺课天数无空间聚集现象,但过离散现象可能存在,可通过软件分析后判断。
条件4:自变量之间无多重共线性。该条件需要通过软件分析后判断。
条件5:自变量不存在显著的异常值。由于本研究所分析的自变量为分类变量,暂不用查看异常值。
三、软件操作及结果解读
(一) 导入数据
mydata <- read.csv("负二项回归.csv") #导入CSV数据
View(mydata) #查看数据
在数据栏目中可以查看全部数据情况,数据集中共有5个变量和146个观察数据,5个变量分别为民族(Race)、性别(Sex)、年龄(Age)、学习状况(Study)及缺课天数(Days)。
如果数据集较大也可使用如下命令查看数据框结构:
str(mydata) #查看数据框结构
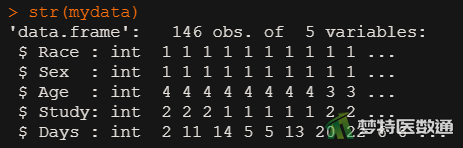
(二) 适用条件判断
1. 条件3判断(过离散检验)
(1) 软件操作
过度离散是残差偏差相对于自由度较大的情况。一个指导原则是,如果残差偏差与残差自由度的比值远远大于1,则模型过度离散。首先建立泊松回归模型,判断是否存在过离散现象。
fit<-glm(Days~Race+Sex+Age+Study,data=mydata,family=poisson()) #建poisson回归模型 summary(fit) #查看回归模型参数
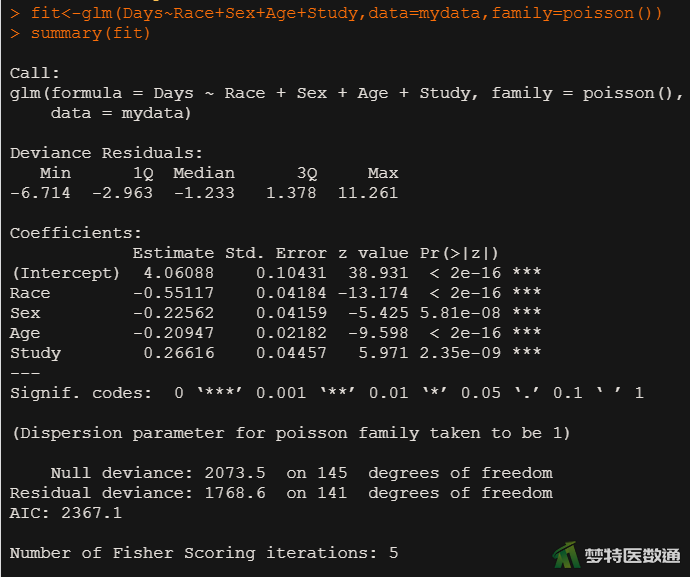
c<-deviance(fit)/df.residual(fit) #计算残差偏差与残差自由度的比值 c #输出残差偏差与残差自由度的比值
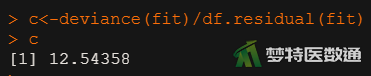
(2) 结果解读
由图4可知,残差偏差与残差自由度的比值等于12.54358,远远大于1,表示因变量存在过离散现象,数据满足条件3。本案例也可计算因变量Days的均数为16.459,方差为264.167,方差远大于均数,也提示因变量存在过离散现象。
2. 条件5判断(多重共线性诊断)
(1) 软件操作
变量之间的共线性诊断可以采用容忍度法 (Tolerance)、方差膨胀因子法 (VIF)、相关系数法和条件数法。本案例采用方差膨胀因子法来查看变量之间的多重共线性,可在线性回归后计算方差膨胀因子。结果如图5所示。
install.packages("car") #安装car包
library(car) #加载car包
lm.nb<-lm(Days~ Race+Sex+as.factor(Age)+Study,data=mydata) #建立线性回归模型
vif(lm.nb) #计算VIF
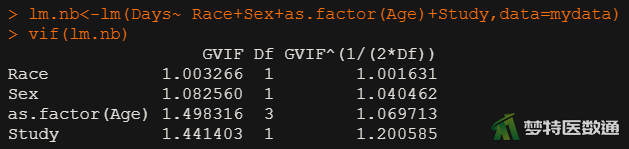
(2) 结果解读
图5结果中列出了自变量的方差膨胀因子(VIF)。可见,四个自变量的VIF均远小于10,提示变量间不存在严重的多重共线性,可知满足条件4。
(三) 统计描述及推断
(1) 软件操作
library(MASS) #加载MASS包 model.nb<-glm.nb(Days~Race+Sex+Study+as.factor(Age),data=mydata) #建立负二项回归模型 summary(model.nb) #输出模型结果 exp(coef(model.nb)) #计算IRR值 exp(confint(model.nb)) #计算IRR值的95%置信区间
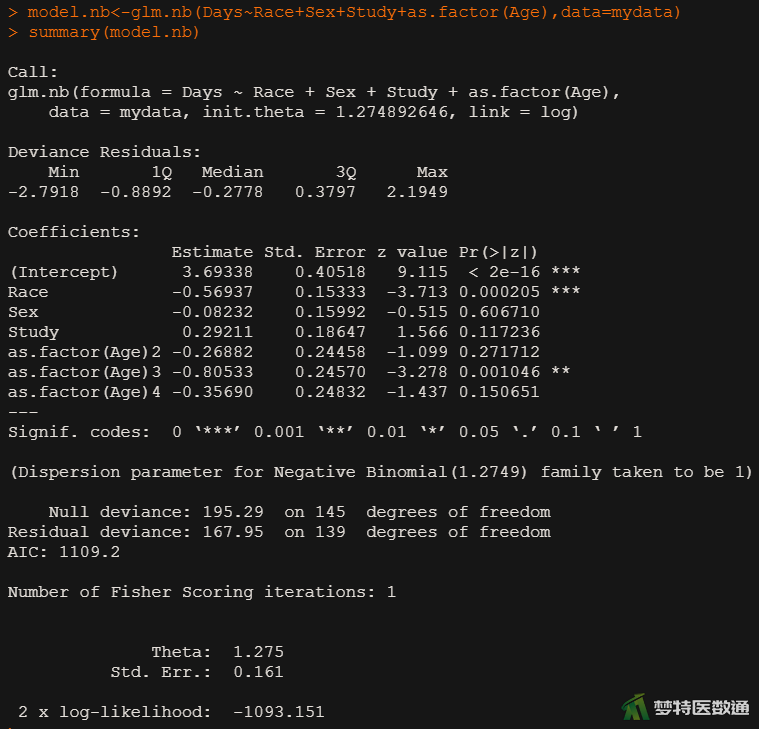
(2) 结果解读
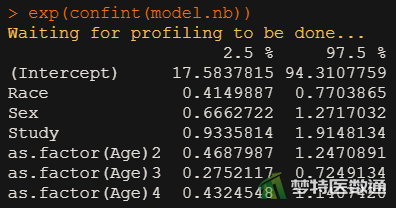
如图6所示,Race和Age3的参数估计值有统计学意义(P<0.05),Race的参数估计值为-0.569,Age3的参数估计值为-0.805。如图7、图8所示,与汉族相比,少数民族学生缺课的发生率是汉族学生的0.566倍(IRR=0.566, 95%CI:0.415-0.770, P<0.001),关联有统计学意义。年龄6-8岁与10-12岁者相比,缺课的发生率下降了0.553倍(IRR=0.447,95%CI:0.276-0.725,P=0.001),关联有统计学意义。

四、结论
本研究采用负二项回归探究民族、性别、年龄和学习状态对学生年缺课天数的影响。通过Poisson回归的过离散指标可知,因变量存在过离散现象;通过共线性诊断可知,变量间不存在严重的多重共线性,满足负二项回归的条件。
由负二项回归分析的结果可知,民族和年龄在模型中有统计学意义(P<0.05),与学生年缺课天数相关。其中,少数民族学生缺课的发生率是汉族学生的0.566倍(IRR=0.566,95%CI:0.415-0.770,P<0.001);年龄6-8岁的与10-12岁的相比,缺课的发生率下降了0.553倍(IRR=0.447,95%CI:0.276-0.725,P=0.001)。
五、知识小贴士
(一) Poisson回归与负二项回归
- Poisson回归的应用条件之一是计数因变量服从Poisson分布,即因变量的平均值等于方差。但很多事件的发生是非独立的,如传染性疾病、地方病、遗传病等,单位时间/空间内事件发生频数的方差远远大于平均值,即存在过离散现象。若用Poisson回归来分析这些事件的影响因素,会导致模型参数估计值的标准误偏小,参数检验的假阳性率增加。这时候宜选择负二项回归进行分析。
(二) 与线性回归的重要区别
- 因变量的变量类型:Poisson回归/负二项回归的因变量为单位时间/空间发生的事件数,为服从Poisson分布或负二项分布计数资料;一般线性回归的因变量为服从正态(高斯)分布计量资料,如BMI、尿量等。
- 在广义线性模型中,Poisson回归/负二项回归的连接函数为ln,即对方程左侧取对数;而线性回归的为恒等函数,不需要任何变换,直接等于右侧的线性组合。
(三) IRR的含义
- IRR,为Incidence rate ratio的缩写,译为发病率的比值,是暴露组与非暴露组事件发生率的比值。当IRR>1时,说明暴露增加了事件发生的可能性;当IRR=1,说明暴露与事件的发生无关联;当IRR<1,说明暴露降低了事件发生的可能性。