二分类Logistic回归分析(Binomial Logistic Regression Analysis)——jamovi软件实现

关键词：jamovi; 二分类logistic回归; 二项logistic回归; 二元logistic回归; 逻辑回归; EPV原则

一、案例介绍

探讨经皮内镜下腰椎间盘摘除术治疗腰椎间盘突出疗效不佳的主要影响因素，纳入经该手术治疗的患者424例，随访12个月观测治疗效果，预后不佳记录为“1”，预后良好记录为“0”；其余变量及编码为性别(0=女，1=男)、年龄(0=60岁以下，1=60岁及以上)、手术时间(min)、突出部位(1=单侧，2=中央，3=极外侧)、突出分类(1=膨出型，2=突出型，3=脱垂型)、Modic改变(1=I级，2=II级， 3=III级)、是否钙化(0=未钙化，1=钙化)、矢状径(cm)、退变级别(1=I-III级，2=IV级，3=V级)。对数据的变量进行标签赋值后部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是探讨经皮内镜下腰椎间盘摘除术治疗腰椎间盘突出疗效不佳的主要影响因素，由于因变量是二分类变量，因此可以使用二分类logistic回归分析。但需要满足7个条件：

条件1：因变量为二分类变量。本研究中因变量是治疗效果“不佳”和“良好”，为二分类变量，该条件满足。

条件2：至少有1个自变量。自变量可以是分类变量也可以是连续变量。本研究中有多个自变量，类型各异，该条件满足。

条件3：各观测行间相互独立。对研究设计和数据收集的过程进行分析，可判断本案例中观测值之间不存在互相影响的情况。

条件4：例数较少类的因变量例数为自变量个数的10~15倍，且经验上两组的人数最好＞30例，参照水平组不应少于30或50例。该条件需要通过软件分析后判断。

条件5：自变量之间无多重共线性。该条件需要通过软件分析后判断。

条件6：自变量不存在显著的异常值。该条件需要通过软件分析后判断。

条件7：数据未出现完全分离或拟完全分离现象。该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件4判断(因变量样本例数)

首先计算因变量中例数较少类的样本例数。

(1) 软件操作

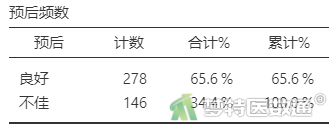
选择“分析”—“探索”—“描述”；将变量“预后”选入“变量”，勾选“频率表格”(图2)，结果如表1所示。

(2) 结果解读

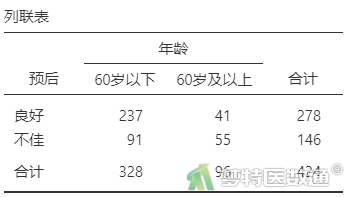
由表1“预后频数”可见，预后不佳为146例，预后良好为278例。根据“例数较少类的因变量例数为自变量个数的10~15倍(EPV原则)”，本案例可纳入10~15个自变量进行多因素二分类logistic回归分析。

2. 条件4判断(自变量样本例数)

逐一计算分类变量各类别的因变量例数。

(1) 软件操作

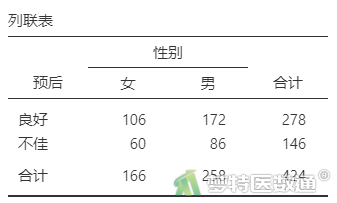
① 选择“分析”—“频数”—“独立样本χ² 关联检验”；将变量“预后”选入“行”，“性别”选入“列”(图3)，结果如表2所示。

② 参照上述操作，依次考察其他变量的频数分布情况，结果如表2—表8所示。

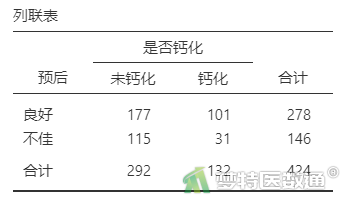
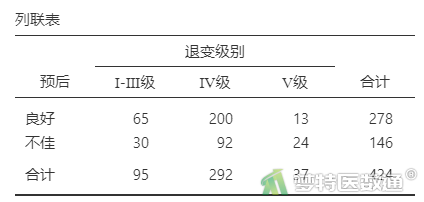
(2) 结果解读

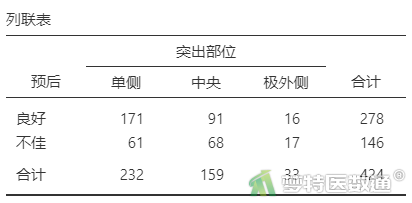
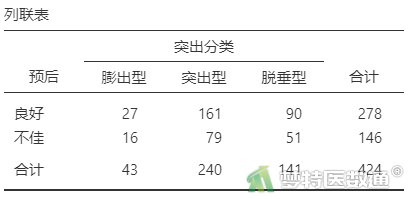
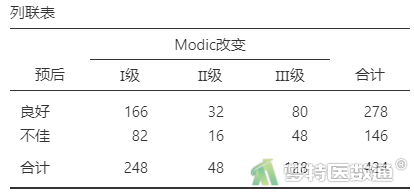
由表2—表8“列联表”可知，突出部位水平为“极外侧”时、突出分类水平为“膨出型”时、退变级别水平为“V级”时，因变量的例数<30，如果这些变量在多因素分析过程中进入模型，一般应注意避免例数较少的水平被选为参照。

3. 条件5判断(多重共线性诊断)

详见本章后文。

4. 条件6判断(异常值检测)

详见本章后文。

5. 条件7判断(完全分离检测)

完全分离，指某一个自变量本身或者某几个自变量的线性组合，对因变量的预测结果与实际情况完全一致，常表现为OR值无穷大。通过表2—表8可见并不存在这种情况。该条件满足。

(二) 变量筛选

1. 软件操作

① 选择“分析”—“回归”，在“Logistic回归”中选择“二分类结局”；将“预后”选入“因变量”，将连续变量“手术时间”、“矢状径”选入“协变量”，将分类变量“性别”、“年龄”、“突出部位”、“突出分类”、“Modic改变”、“是否钙化”、“退变级别”选入“因子”，见图4。

② 在“建模”中，分别按次序为每个自变量创建一个“层”，并将自变量选入块层中，本案例需要创建9层，见图5。

③ 在“参考水平”下，为分类变量选择合适的参考水平，根据条件4(自变量样本例数)计算结果，突出部位水平为“极外侧”时、突出分类水平为“膨出型”时、退变级别水平为“V级”时，因变量的例数<30，应注意避免这三个变量中例数较少的水平被选为参照，见图6。

④ 在“模型拟合”下的“拟合评价”中勾选“整体模型检验”(图7)，结果如表9所示；在“模型系数”下的“整体检验”中勾选“似然比检验”(图7)，结果如表10所示。

2. 结果解读

由于本案例分析过程中创建了9个块，所以一共会生成9个模型。表9“模型拟合评价”分别显示了每个模型的检验结果，可见除了模型1以外，其他模型均有统计学意义，说明除了模型1以外，其他模型中都至少存在一个自变量具有统计学意义。模型1中只有一个自变量“手术时间”，也表明该自变量没有统计学意义。

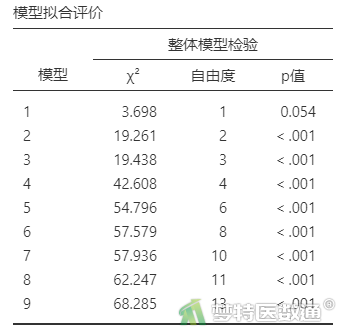
表10“Omnibus似然比检验”中列出了每个自变量在模型中是否有统计学意义，即是否应被纳入模型。可知，“手术时间”、“性别”、“突出分类”、“Modic改变”四个变量无统计学意义，应该被移除模型。

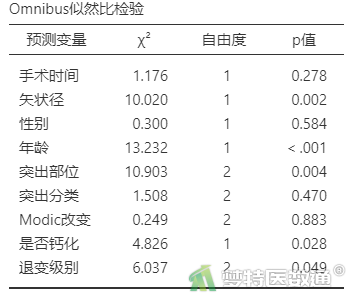
表11“模型对比”中列出了每个模型新增一个自变量后与上一个模型相比差异是否有统计学意义，也即表示新加入的变量是否有统计学意义。可知，模型3与模型2相比差异无统计学意义，说明第3个块中的变量无统计学意义，即变量“性别”无统计学意义。依次推理，可知第6和第7个块中的变量无统计学意义，即变量“突出分类”和“Modic改变”无统计学意义。可见，表11与表10等价。

(三) 适用条件判断(补充)

将“手术时间”、“性别”、“突出分类”、“Modic改变”四个无统计学意义的变量及其“层”从“建模”中移除后进行如下操作。

1. 条件5判断(多重共线性诊断)

(1) 软件操作

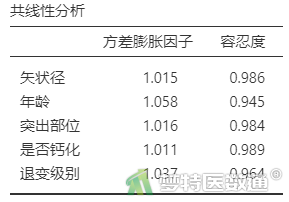
在“适用条件判断”中勾选“共线性分析”(图8)，结果如表12所示。

(2) 结果解读

表12“共线性诊断”结果中列出了自变量的方差膨胀因子和容忍度。可见，所有自变量的VIF均<10，容忍度均>0.1，提示自变量之间不存在严重共线性问题。

2. 条件6判断(异常值检测)

(1) 软件操作

① 在“保存”中勾选“Cook’s距离” (图9)，则在数据视图界面会产生5列新的变量“Cook's距离 - 1”—“ Cook's距离 - 5”，即每个模型产生一列库克距离值。

② 选择“分析”—“探索”—“描述”，将模型5的库克距离“Cook's距离 - 5”选入右侧“变量”框(图10)。

③ 在“统计”下的“样本量”中勾选“个案数”、“缺失”，在“集中趋势”中勾选“均值”、“中位数”，在“离散”中勾选“标准差”、“最小值”和“最大值”(图11)，结果如表13所示。

(2) 结果解读

从表13“描述”表格可见，最大的库克距离值为0.031<0.5，提示不存在显著异常值，本研究数据满足条件6。

(四) 模型拟合

1. 软件操作

如图12，勾选“模型拟合”和“模型系数”下的所有选项。

2. 结果解读

(1) 拟合优度

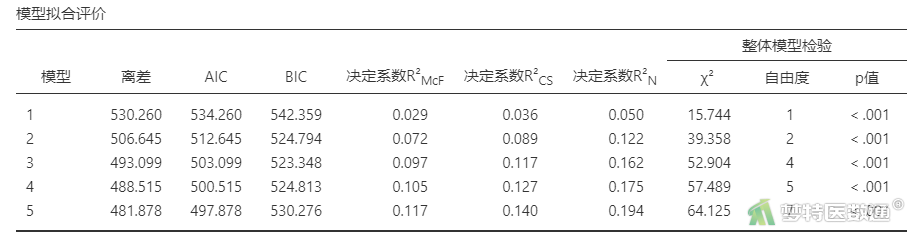
表14“模型拟合评价”结果，列出了5个模型的“残差”、“AIC”、“BIC”、“决定系数R²_McF”、“决定系数R²_CS”、“决定系数R²_N”和“模型整体检验”。

AIC和BIC均是衡量统计模型拟合优良性的指标，其值越小越好。“R²_McF”、“R²_CS”、“R²_N”均说明的是回归方程对解释变量变异量化的指标，越接近1说明回归方程的拟合度越高。“R²_McF”介于0.2-0.4之间代表模型拟合的较好，因此本数据集模型拟合度不高。“模型整体检验”采用的是似然比卡方检验对模型进行参数检验，考察模型的整体显著性，可见5个模型均有统计学意义，表示5个模型中均至少有1个自变量具有统计学意义。

(2) 模型系数

从表15“模型对比”和表16“Omnibus似然比检验”可见，模型5中所有自变量均有统计学意义。

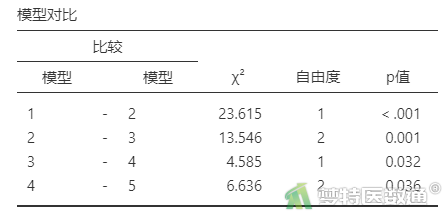
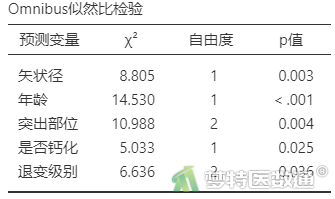
表17“模型系数 – 预后”表格列出了各自变量拟合后在模型4中的“系数”及其95%置信区间、“标准误”、“Z值”、“P值”、“比值比”及其95%置信区间。比值比为e^{(回归系数)}，如矢状径的比值比=0.836=e^(-0.179)，表示矢状径每增加1cm，术后效果不佳的风险降低16.4% (比值比=0.836，95%CI：0.740~0.944；P=0.004)。

其他自变量结果的解释分别为，年龄60岁及以上的患者术后不佳的风险是60岁以下患者的2.780倍(95%CI：1.643~4.702；P<0.001)。突出部位为“中央”和“极外侧”的患者术后效果不佳的风险分别是“单侧”患者的2.091倍(95%CI：1.318~3.318；P=0.002)和2.133倍(95%CI：0.922~4.936；P=0.077)。“非钙化”患者术后不佳的风险是“钙化”患者的1.743倍(95%CI：1.064~2.855；P=0.027)。与退变级别为“V级”的患者相比，“I-III级”患者术后效果不佳的风险降低54.1% (95%CI：0.184~1.147；P=0.096)；“IV级”患者术后效果不佳的风险降低63.7% (95%CI：0.163~0.809；P=0.013)。

(五) 预测价值

1. 软件操作

在“预测”下勾选所有选项(图13)。

2. 结果解读

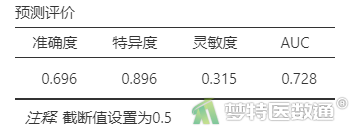
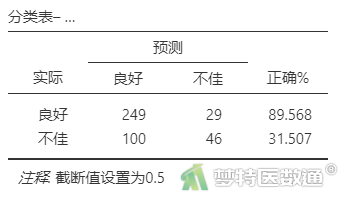
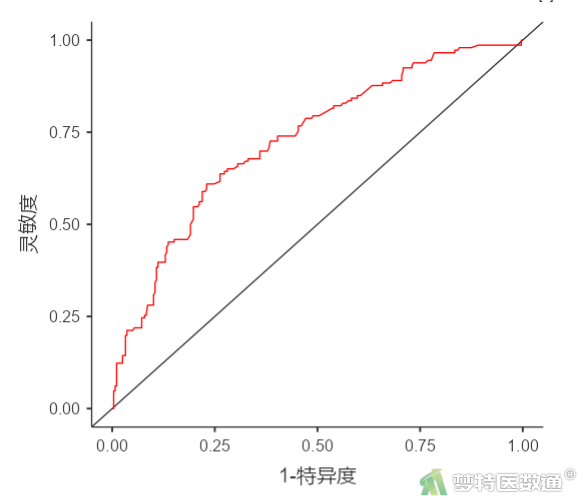
表18“预测评价”显示了自变量对因变量正确分类的“准确度”、“特异度”、“灵敏度”和“AUC”，可见进入模型的5个变量对因变量正确分类的准确度为69.6%，灵敏度为31.5%、特异度为89.6%，AUC为72.8%，该模型的判断效果一般。

四、结论

本研究采用二分类Logistic回归探讨经皮内镜下腰椎间盘摘除术治疗腰椎间盘突出疗效不佳的主要影响因素。因变量例数分布满足样本量需求，变量之间不存在严重共线性和异常值，数据不存在完全分离现象。

9个自变量经过分析后，最终有5个(矢状径、年龄、突出部位、是否钙化和退变级别)进入模型，其中矢状径每增加1cm，术后效果不佳的风险降低16.4% (OR=0.836，95%CI：0.740~0.944；P=0.004)；年龄60岁及以上的患者术后不佳的风险是60岁以下患者的2.780倍(95%CI：1.643~4.702；P<0.001)；突出部位为“中央”和“极外侧”的患者术后效果不佳的风险分别是“单侧”患者的2.091倍(95%CI：1.318~3.318；P=0.002)和2.133倍(95%CI：0.922~4.936；P=0.077)；“非钙化”患者术后不佳的风险是“钙化”患者的1.743倍(95%CI：1.064~2.855；P=0.027)；与退变级别为“V级”的患者相比，“I-III级”患者术后效果不佳的风险降低54.1% (95%CI：0.184~1.147；P=0.096)；“IV级”患者术后效果不佳的风险降低63.7% (95%CI：0.163~0.809；P=0.013)。所建立的模型有统计学意义(χ²=64.125，P<0.001)，对因变量正确分类的准确度为69.6%，灵敏度为31.5%、特异度为89.6%，AUC为72.8%，该模型的判断效果一般。

五、多重共线性的判断及处理

(一) 多重共线性的概念

• 多重共线性是指自变量间存在线性相关关系，容忍度越小、VIF越大，表明共线性越强。实际数据分析过程中，若容忍度<0.2或VIF＞5则表明存在较强共线性，若容忍度<0.1或VIF＞10则表明存在严重共线性问题。需要注意的是，多重共线性的存在不一定必然影响模型的使用价值，其理论上共线性不应当降低模型的预测效果，其影响主要是使模型的偏回归系数发生改变，从而无法得到专业上合理的解释。

(二) 多重共线性的识别

在实际数据分析过程中，若存在以下情况，则暗示模型可能存在共线性问题：

• 整个模型的检验结果为P值≤检验水准a，但各自变量的偏回归系数检验结果却为P值＞检验水准a。
• 专业上认为应该有统计学意义的自变量，检验结果确无统计学意义。
• 自变量的偏回归系数的取值大小甚至符号明显与实际情况相违背，难以解释。
• 增加或删除一个自变量或一个样本，自变量偏回归系数发生较大变化。

(三) 多重共线性的处理

自变量若存在严重多重共线性，可采取以下措施进行处理：

• 基于专业知识直接确认优先选择哪些变量进入模型，而将相对次要的共线性变量从模型中剔除。
• 逐步回归，但是当共线性比较严重时，变量自动筛选的方法并不能完全解决问题。
• 岭回归/lasso回归，为有偏估计，但能有效地解决共线性问题。
• 主成分回归法，这种方法的代价是在提取主成分时会丢失一部分信息，收益则是大大降低了共线性对参数估计值的扭曲，而且自变量间的多重共线性越强，提取主成分时丢失的信息就越少。

六、自变量的选择策略

关于自变量是否纳入多因素分析模型除了根据本章节介绍的判定方法以外，还可采取以下策略：

• 专业原则：首先需要考虑的就是专业原则，这一点最为重要。如果目前专业知识有证据表明该变量与结局发生有关，那么无论该变量单因素分析结果是否有统计学意义，都应纳入多因素分析模型。
• 以单因素分析为基础：当分析的变量较多时，可先采取单因素分析方法，对有统计学意义的变量再纳入多因素分析。此时单因素分析检验水准可设置为0.1—0.2，如果样本量较大，可将检验水准设置为较为宽松；如果样本量较小可将检验水准设置较为严格。
• 比较原则：可以尝试多种方法对该变量进行分析，如采用多种自变量进入方法分析，或将计量资料降维后再分析，如果变量在多种进入方法和不同变量类型时，均能在多因素分析模型中有统计学意义，则表明该变量的确是因变量的真正影响因素。

七、自变量进入模型的形式

(一) 无序多分类自变量

无序多分类自变量需要以哑变量形式进入模型，在jamovi中通过选择参照水平实现哑变量的设置，但需要注意以下事项：

• 参照水平要具有实际意义，否则会失去比较的目标，如“其他”一般不适宜做参照水平。
• 参照水平应有一定的例数(最好不低于30或50例)，否则将导致与其比较的其他组的置信区间较大。
• 哑变量整体分析无统计学意义时，所有哑变量都不用再纳入模型；整体分析有统计学意义时，尽管有些哑变量无统计学意义，但仍需要纳入模型，即“同进同出”原则。

(二) 有序多分类自变量

有序多分类自变量进入模型有多种方式备选，但应选择最具合理性的方式。

• 直接以计量资料形式带入模型：此时得到的模型较为简洁，也容易解释。但应用的前提是自变量的每个水平对因变量的影响作用基本一致，可通过观察哑变量各水平的回归系数值是否存在等级变化关系进行判定。建议先将有序多分类资料分别以哑变量和连续变量的形式引入模型，观察每个哑变量的回归系数间是否存在等级关系，并对两个模型进行似然比检验，如果似然比检验无统计学意义，且每个哑变量的回归系数间存在等级关系，则可以将该自变量以连续变量形式引入模型，否则还是采用哑变量的方式引入模型。
• 设置哑变量：参照无序多分类资料。
• 当有序多分类变量的等级水平与因变量结局不成线性关系时，应采用最优尺度回归探讨效应拐点。

(三) 计量资料

计量资料进入模型有多种方式备选，但也应选择最具合理性的方式：如果某计量资料能以计量形式进入模型(有统计学意义)，那么转化后应当同样能进入模型，且OR值会显著增加。

• 直接带入模型，尽管此种方法较为简单，但仍不做首选推荐。因为此时得出的OR值一般较小，即自变量变化一个单位对结局风险的影响其实是有限的，不能贴近专业解释。 如果资料分布严重失衡时(非均匀分布)尤其不能直接带入模型。但以计量资料形式直接进入模型往往模型的拟合效果较好。
• 根据专业意义降维后(如根据BMI指数分级标准降维为有序多分类资料)，参照有序多分类资料或者二分类资料处理方式。
• 如果没有专业划分标准，可以资料分布形式根据四分位数间距或等分法降维或者标准化后按每一个标准差降维。
• 建立自变量和因变量之间的ROC曲线，根据约登指数进行二分类降维。
• 中位数(非正态分布)或者均数(近似正态或正态分布)降维。⑥当自变量的单位不合适导致因变量的风险改变很小时，可对自变量采取缩小(如除以100)或扩大(如乘以10)相应倍数的方式。

八、AIC和BIC

• AIC和 BIC均是衡量统计模型拟合优良性的指标，其值越小越好。
• AIC建立在熵的概念基础上，可以权衡所估计模型的复杂度和此模型拟合数据的优良性。BIC的惩罚项比AIC的大，考虑了样本数量，样本数量过多时，可有效防止模型精度过高造成的模型复杂度过高。AIC和BIC的原理是不同的，AIC是从预测角度，选择一个好的模型用来预测，BIC是从拟合角度，选择一个对现有数据拟合最好的模型，从贝叶斯因子的解释来讲，就是边际似然最大模型。