简单线性回归分析(Simple Linear Regression Analysis)——jamovi软件实现

关键词：jamovi; 简单线性回归; 直线回归; 残差齐性检验; 残差正态检验; 哑变量设置

一、案例介绍

研究健康成年人的体重和双肾脏总体积(ml)的关系，测得24名健康成年人的体重wt (kg)与双肾脏总体积volume (ml)，拟探讨健康成年人的体重与双肾总体积是否有关，并希望通过健康成年人的体重预测双肾总体积。对数据的变量进行标签赋值后部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是通过判断两个计量资料之间的关系，同时使用其中一个变量预测另一个变量，计算其中一个变量对另一个变量变异的解释程度。针对这种情况，可以使用简单线性回归分析。但需要满足7个条件：

条件1：因变量为连续变量。本研究中，健康成年人的体重为连续变量，该条件满足。

条件2：自变量可以被定义为连续变量，人体双肾总体积为连续变量，该条件满足。

条件3：两个变量之间存在线性关系。该条件需要通过软件分析后判断。

条件4：各观测值之间相互独立，即残差之间不存在自相关。通过研究设计和数据收集的过程分析，可判断本案例中观测值之间不存在互相影响的情况。该条件还可通过软件分析后辅助判断。

条件5：自变量不存在显著的异常值，该条件需要通过软件分析后判断。

条件6：残差符合正态(或近似正态)分布，该条件需要通过软件分析后判断。

条件7：残差方差齐。该条件需要通过软件分析后判断。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件3判断(因变量和自变量之间存在线性关系)

(1) 软件操作

选择“分析”—“探索”—“散点图”，将变量“体重”选入“X轴”框，将变量“双肾体积”选入“Y轴”框，在“回归线”中勾选“线性”和“标准误”(图2)，结果如图3所示。

(2) 结果解读

由图3可见，散点大致呈一条直线，提示变量“体重”和“双肾体积”存在线性关系，满足条件3。

2. 条件4判断(各观测值之间相互独立)

(1) 软件操作

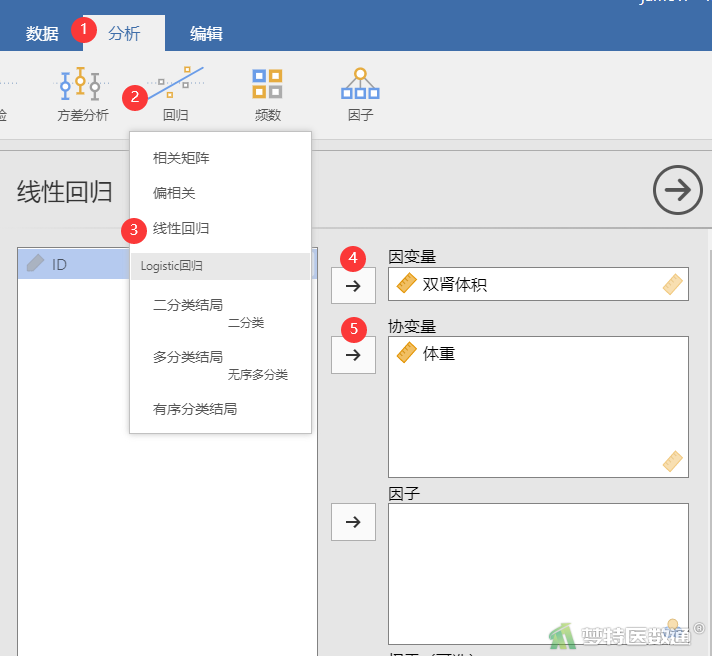
① 选择“分析”—“回归”—“线性回归”，将变量“双肾体积”选入“因变量”框，将变量“体重”选入“协变量”框(图4)。

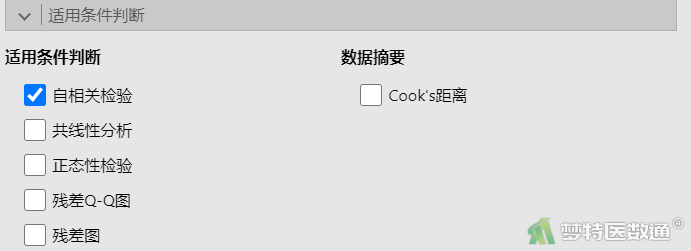
② 在“适用条件判断”中勾选“自相关检验”(图5)，结果如表1所示。

(2) 结果解读

表1“Durbin–Watson自相关检验”显示，DW统计量为2.078，P=0.844，说明观测值相互独立，本研究数据满足条件4。

3. 条件5判断(异常值检测)

通过图3的散点图可见，数据不存在异常值。但仍需要统计分析结果的判断。

(1) 软件操作

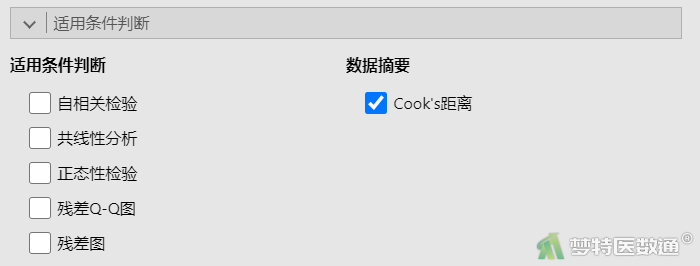
在“适用条件判断”中勾选“Cook’s距离”(图6)，结果如表2所示。

(2) 结果解读

表2“Cook’s距离”表格显示，最大库克距离D为0.285<0.5，提示不存在显著异常值，本研究数据满足条件5。

4. 条件6判断(残差近似正态分布)

(1) 软件操作

在“适用条件判断”中勾选“正态性检验”和“残差Q-Q图”(图7)，结果如表3和图8所示。

(2) 结果解读

表3“正态性检验(Shapiro-Wilk)”显示，P=0.506>0.1，提示残差服从正态分布。图8残差的Q-Q图中各散点基本围绕对角线分布，也提示残差服从正态分布，本研究数据满足条件6。

5. 条件7判断(残差的方差齐)

(1) 软件操作

在“适用条件判断”中勾选“残差图” (图9)，结果如图10-1—图10-3所示。

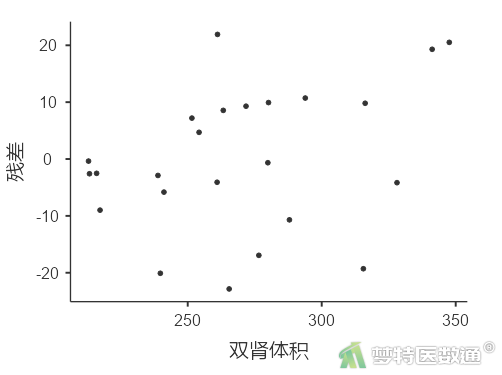
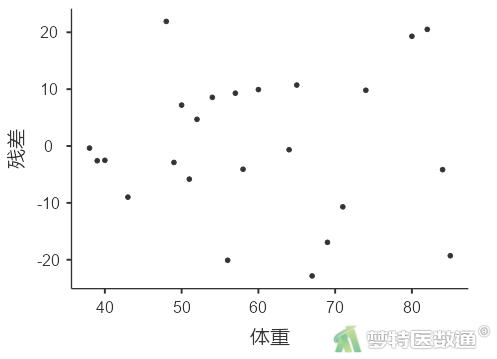
(2) 结果解读

图10-1—图10-3中预测值和各变量值的残差分布较为均匀，并未出现特殊的分布形式(如漏斗或者扇形)，提示残差的方差齐，本研究数据满足条件7。

(二) 模型拟合

1. 软件操作

在“模型拟合”和“模型系数”中按图11勾选相应选项。

2. 结果解读

(1) 模型拟合程度

表4“模型拟合评价”列出了拟合后模型的各项参数。

R是复相关系数，当简单线性回归中只有一个自变量时，R值与因变量和自变量的Pearson相关系数相同，代表两者之间的相关程度。本研究中R=0.947，提示两者之间为强相关。决定系数R²=0.896，提示自变量 (体重)可以解释89.6%的因变量的变异 (双肾总体积)，但是R²会受自变量个数的影响，夸大自变量对因变量变异的解释程度，自变量越多，R²越大。校正R²调整了自变量个数对结果的影响，一般小于R²。校正R²=0.891，提示自变量 (体重)可以解释89.1%的因变量的变异 (双肾总体积)。

AIC为赤池信息量准则，BIC为贝叶斯信息准则，两者均是衡量统计模型拟合优良性的一种标准，其值越小越好。均方根误差的值越小越好。

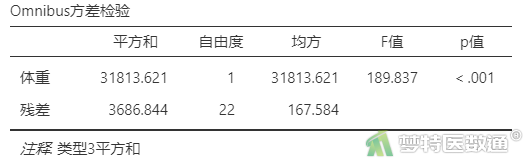
“整体模型检验”结果显示F=189.837，P<0.001，提示模型有意义。如果P>0.05，则说明回归没有统计学意义。等价于表5的“Omnibus方差检验”结果。

(2) 回归系数解释

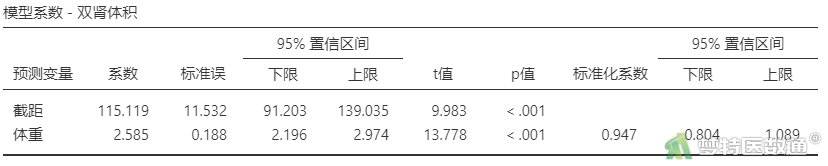
表6“模型系数- 双肾体积”列出了截距和自变量的“系数”、“标准误”及95%置信区间，t值及P值，以及“标准化系数”及95%置信区间。可知，回归模型的截距为115.119，表示自变量取值为0时，因变量的取值，并无实际专业意义。变量“体重”的非标准化系数(即斜率)为2.585 (95%CI：2.196~2.974)，表示体重每增加1kg，双肾体积增加2.585ml。据此可以写出本案例的回归方程为：

根据此方程可以计算合理范围内体重对应的双肾总体积。

四、结论

本研究采用简单线性回归模型通过健康成年人的体重预测双肾总体积。通过绘制散点图，提示两者之间存在线性关系；通过专业判断和Durbin-Watson检验提示数据之前相互独立；通过绘制散点图和库克距离分析，提示数据不存在需要删除的异常值；通过Shapiro-wilk检验及绘制残差Q-Q图，提示残差符合正态分布；通过绘制残差图，提示残差方差齐。本研究数据满足线性回归分析条件。

线性回归分析方程为：双肾体积 = 115.119 + 2.585×体重，回归模型具有统计学意义，F=189.837，P<0.001；自变量(体重)可以解释89.6%的因变量的变异(双肾总体积)，影响程度较高(校正R²=0.891)，即体重每增加1kg，双肾总体积增加2.585 (95%CI：2.196~2.974)ml。

五、知识小贴士

• Durbin-Watson检验通常用来检测残差是否存在自相关，Durbin-Watson检验值分布在0~4之间，越接近2，观测值相互独立的可能性越大。
• 需要注意的是，判断观测值是否独立，主要取决于研究设计和数据收集阶段的质量控制，Durbin-Watson检验最好用于辅助判断。
• 库克距离用来判断强影响点是否为因变量的异常值点。一般认为当D<0.5时不是异常值点，当D>0.5时认为是异常值点。
• 分析中得到的回归截距，即当自变量为0时因变量对应的值，本研究中，回归截距为当体重为0时，研究对象的平均双肾体积为115.119 ml。这显然不符合客观实际，因此，在进行简单线性回归时截距的统计检验结果是否有统计学意义无需过于关注，需要关注的是斜率。
• 在进行回归分析时，要注意避免对数据的过渡挖掘，不能将回归模型分析的结果随意延伸到自变量取值范围以外的数值，也不能随意将模型分析结果延伸到因果关系。