多重线性回归分析(Multiple Linear Regression Analysis)——jamovi软件

关键词：SPSS; 多重线性回归; 多元线性回归; 多重共线性; 自变量选择; 逐步回归; 模型拟合评价; 哑变量设置

一、案例介绍

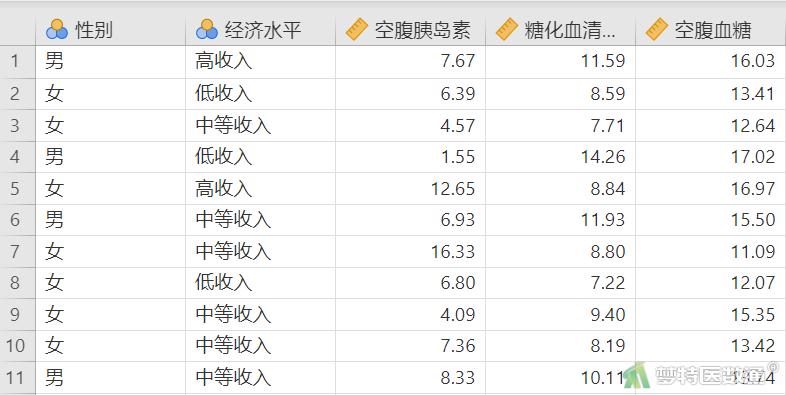
某社区医师从本社区的糖尿病患者中随机抽取50名，收集了他们的性别(Gender)、经济水平(Income)、空腹胰岛素(Fasting insulin，mmol/L)、糖化血清蛋白(Glycosylated serum protein)和空腹血糖(FBS，mmol/L)，欲探究空腹血糖是否受到其他几项指标的影响。部分数据见图1，本案例数据可从“附件下载”处下载。

二、问题分析

本案例的目的是分析空腹血糖是否受到其他几项指标的影响，由于因变量是定量资料，初步考虑可使用多重线性回归分析。但需要满足以下7个条件：

条件1：样本量是自变量个数的5~10倍。本案例有4个自变量，样本量为50，该条件满足。

条件2：自变量若为连续变量，需要与因变量之间存在线性关系，可通过绘制散点图予以考察。

条件3：各观测值之间相互独立，即残差之间不存在自相关。通过研究设计和数据收集的过程分析，可判断本案例中观测值之间不存在互相影响的情况。该条件还可通过软件分析后辅助判断。

条件4：不存在显著的多变量异常值，该条件需要通过软件分析后判断。

条件5：自变量之间无多重共线性，该条件需要通过软件分析后判断。

条件6：残差符合正态(或近似正态)分布，该条件需要通过软件分析后判断。

条件7：残差大小不随所有变量取值水平的变化而变化，即方差齐性，可通过绘制残差图进行判断。

三、软件操作及结果解读

(一) 适用条件判断

1. 条件2判断(连续性自变量与因变量之间的线性关系)

(1) 软件操作

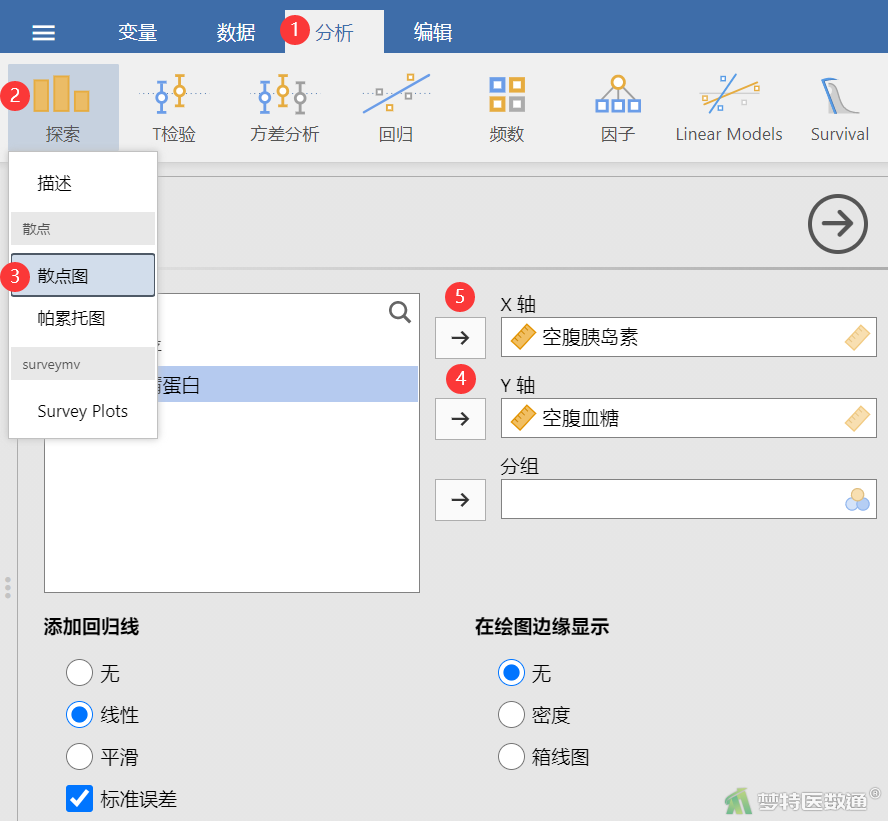
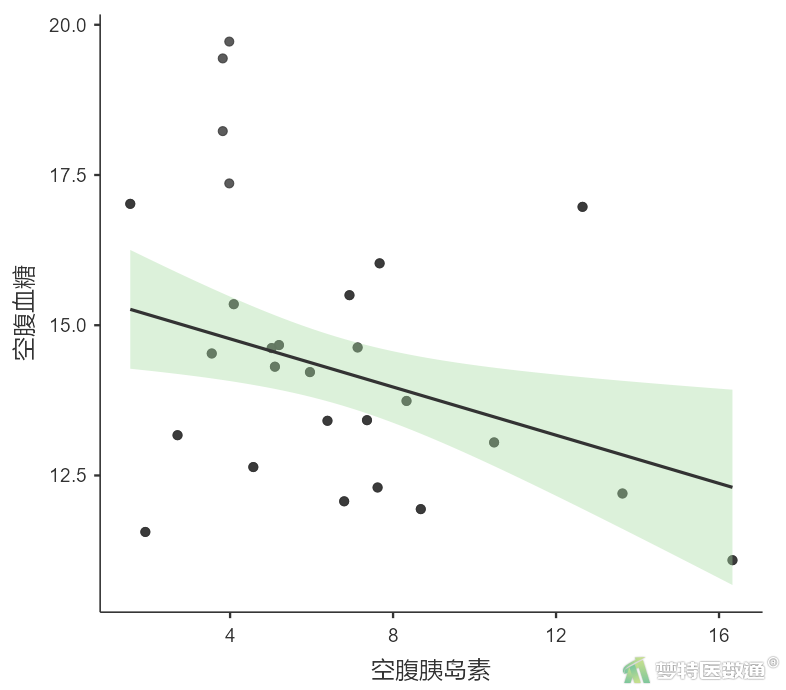
选择“分析”—“探索”—“散点图”，将变量“空腹血糖”选入右侧“Y轴”，将变量“空腹胰岛素”选入右侧“X轴”框，在“添加回归线”中选中“线性”并勾选“标准误差”(图2)，结果见图3。

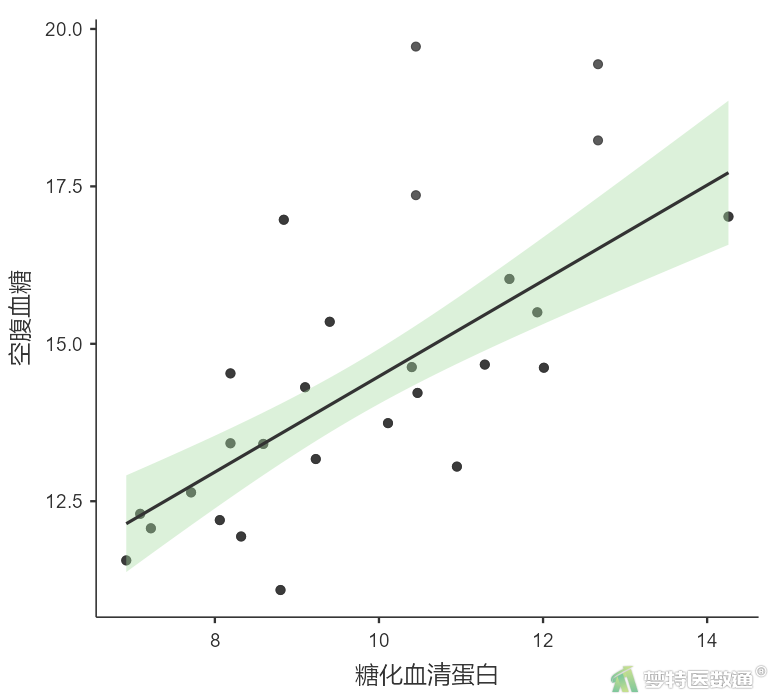
重复上述操作，绘制“糖化血清蛋白”与“空腹血糖”之间的散点图，见图4。

(2) 结果解读

由散点图(图3、图4)可知，“空腹胰岛素”“糖化血清蛋白”与因变量之间均存在线性关系。案例数据满足条件2。

2. 条件3判断(各观察值之间相互独立)

(1) 软件操作

选择“分析”—“回归”—“线性回归”，将变量“空腹血糖”选入“因变量”框，将自变量“性别”和“经济水平”选入“因子”，将“空腹胰岛素”和“糖化血清蛋白”选入右侧“协变量”框(图5)。

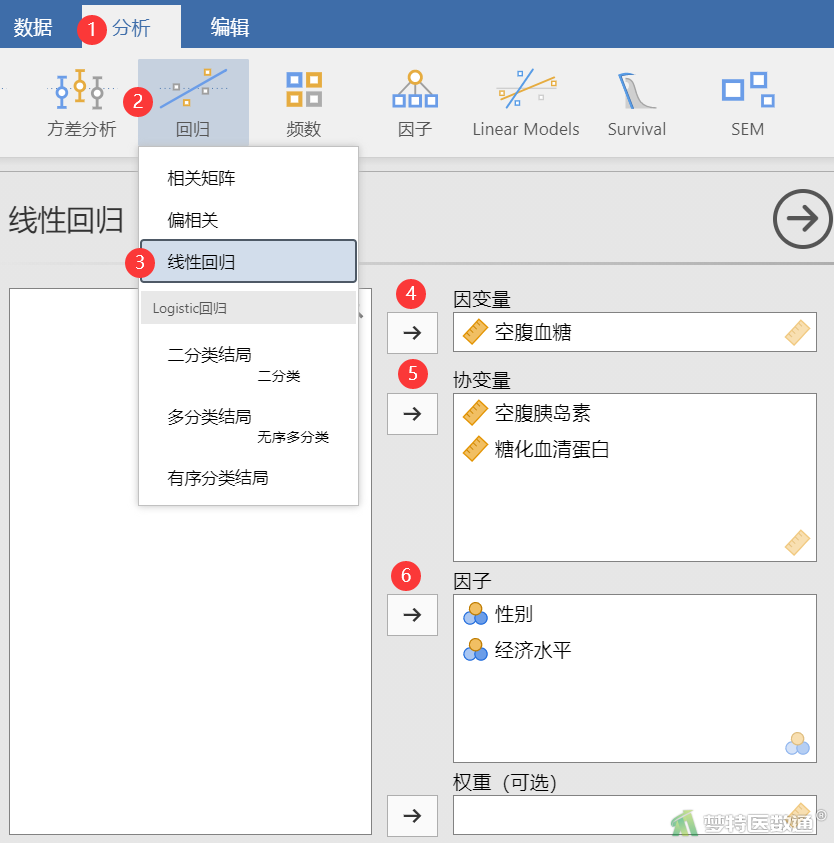
在“适用条件判断”中勾选“自相关检验”(图6)，结果见表1。

(2) 结果解读

“Durbin–Watson自相关检验”结果(表1)显示，DW统计量为1.655，P=0.254，说明观测值相互独立，满足条件3。

3. 条件4判断(不存在显著的多变量异常值)

(1) 软件操作

在“数据摘要”中勾选“Cook’s距离”(图7)，结果见表2。

(2) 结果解读

“Cook’s距离”结果(表2)显示，最大Cook’s距离为0.234<0.5，提示不存在显著异常值，本研究数据满足条件4。

4. 条件5判断(多重共线性判断)

(1) 软件操作

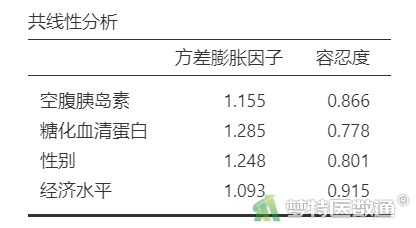
在“适用条件判断”中勾选“共线性分析”(图8)，结果见表3。

(2) 结果解读

“共线性分析”结果(表3)中列出了自变量的方差膨胀因子(variance inflation factor，VIF)和容忍度(Tolerance)。可见，所有自变量的VIF均<5，容忍度均>0.1，提示自变量之间不存在严重共线性问题。

5. 条件6判断(残差符合正态分布)

(1) 软件操作

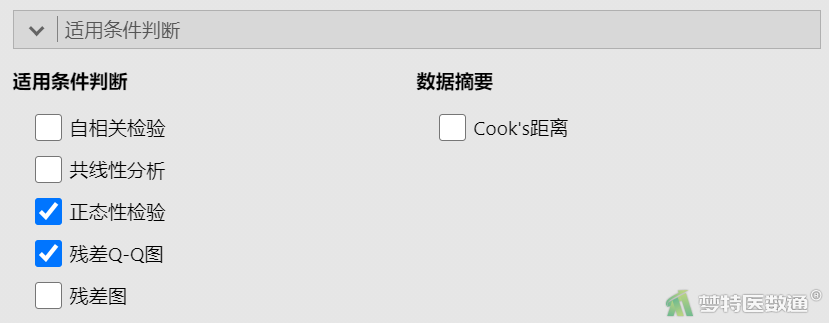
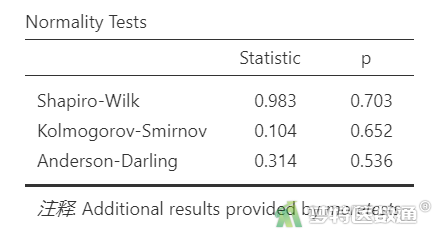
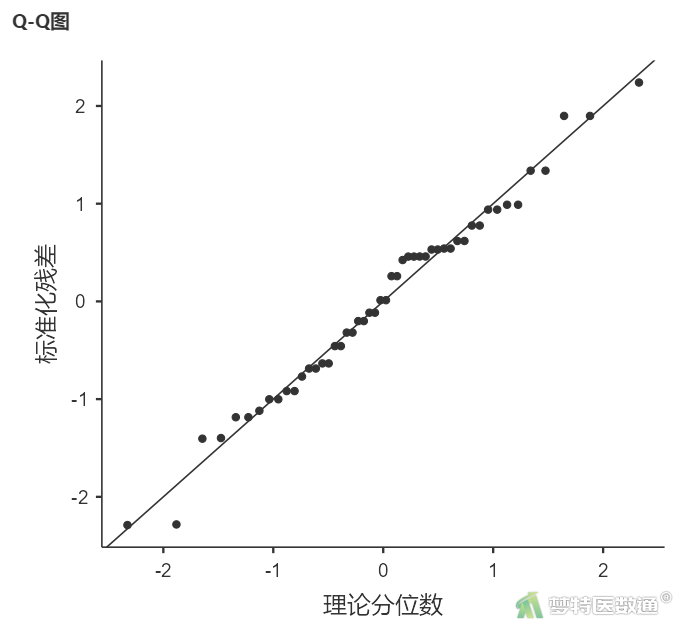
在“适用条件判断”中勾选“正态性检验”和“残差Q-Q图”(图9)，结果见表4、图10。

(2) 结果解读

“Normality Test (正态性检验) ”结果(表4)选择Shapiro-Wilk检验，结果显示，P=0.703>0.1，提示残差服从正态分布。残差Q-Q图(图10)中各散点基本围绕对角线分布，也提示残差服从正态分布。因此，判定本研究数据满足条件6。

6. 条件7判断(方差齐性)

(1) 软件操作

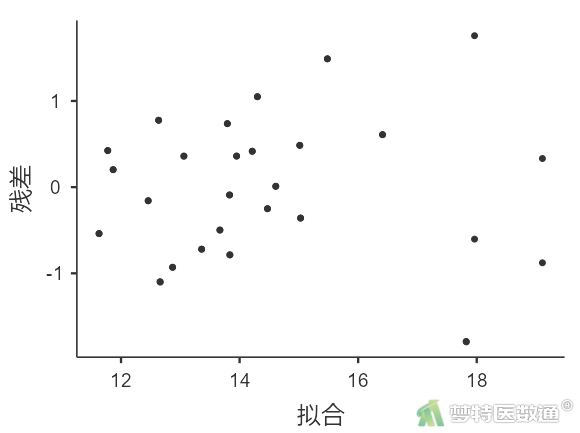
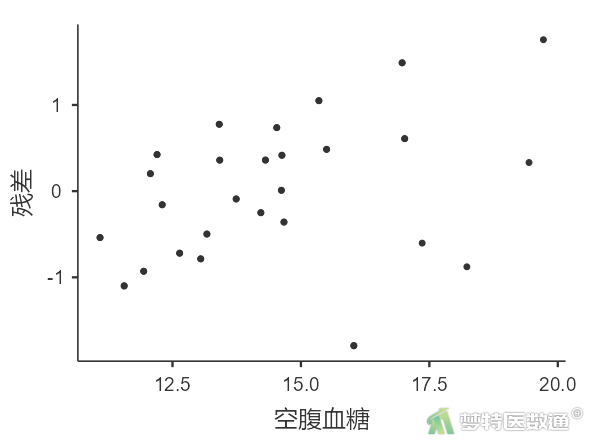
在“适用条件判断”中勾选“残差图”(图11)，结果如图12-1~12-4所示。

(2) 结果解读

图12-1~图12-4中预测值和各变量值的残差分布较为均匀，并未出现特殊的分布形式(如漏斗或者扇形)，提示残差的方差齐，本研究数据满足条件7。

(二) 变量筛选

1. 软件操作

①在“建模”中，分别按次序为每个自变量创建一个“层”，并将自变量选入层中，本案例需要创建4个层(图13)。

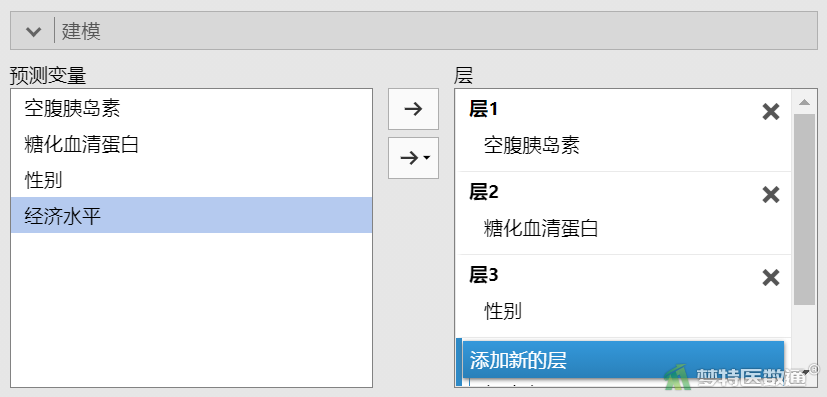
②在“参考水平”中，为分类变量选择合适的参考水平，此处“性别”中选择“女”为参照水平，“经济水平”中选择“低收入”为参照水平(图14)。

③在“模型拟合”下的“整体模型检验”中勾选“F检验”，在“Omnibus检验”中勾选“方差分析”(图15)，结果分别见表5、表6。

2. 结果解读

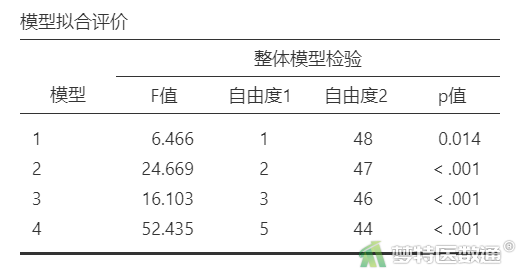
由于本案例分析过程中创建了4个块，所以一共会生成4个模型。“模型拟合评价”结果(表5)分别显示了每个模型的检验结果，可见所有模型均有统计学意义，说明所有模型中都至少存在1个自变量具有统计学意义。

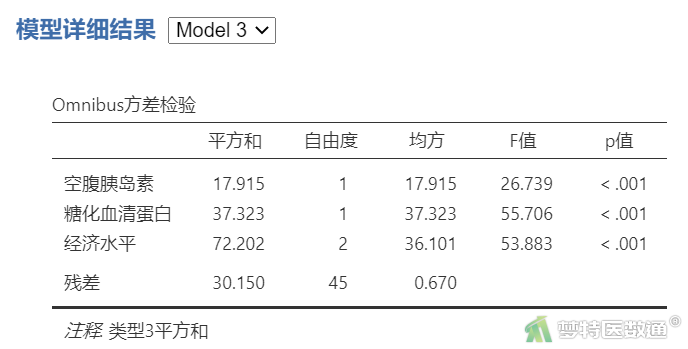
“Omnibus方差检验”结果(表6)中列出了每个自变量在模型中是否有统计学意义，即是否应被纳入模型。可知，变量“性别”无统计学意义，应该被移除模型。

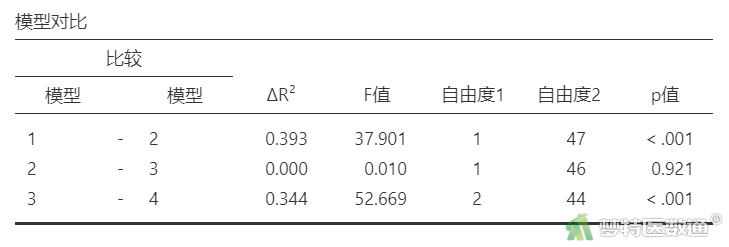
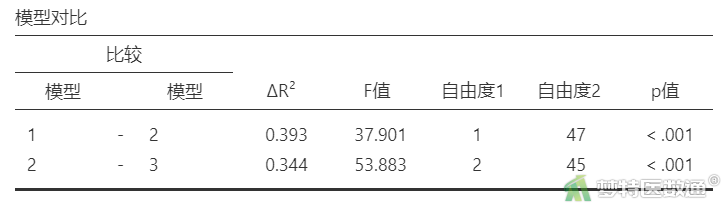
“模型对比”结果(表7)中列出了每个模型新增一个自变量后与上一个模型相比决定系数的差异(ΔR²)是否有统计学意义，也即表示新加入的变量是否有统计学意义。可知，模型3与模型2相比差异无统计学意义，说明第3个块中的变量无统计学意义，即变量“性别”无统计学意义。可见，表7与表6等价。

(三) 模型拟合

将变量“性别”及其“层”从“建模”中移除后进行如下操作。

1. 软件操作

在“模型拟合”和“模型系数”下，勾选所有选项(图16)。

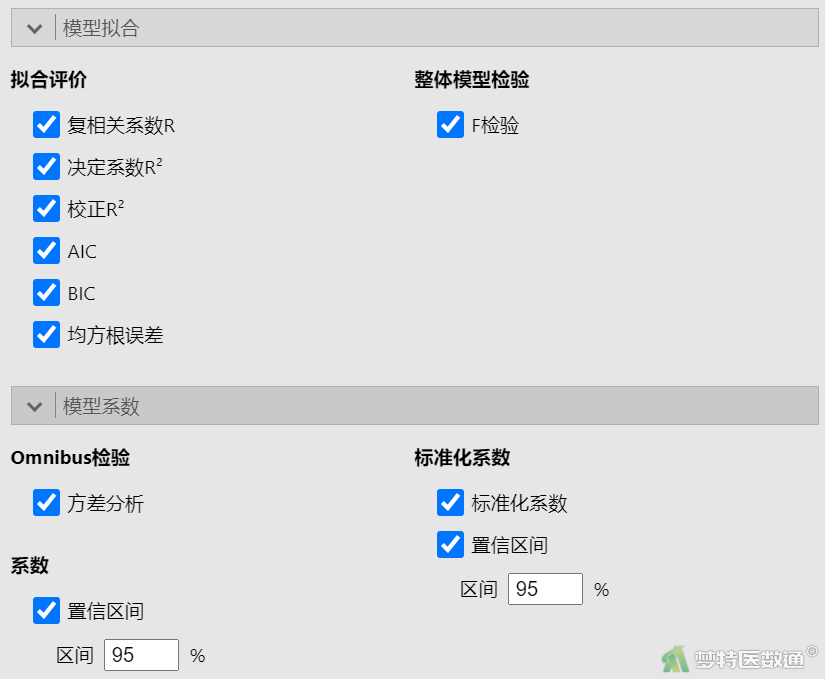
2. 结果解读

(1) 拟合优度

“模型拟合评价”结果(表8)列出了3个模型的“复相关系数R”“决定系数R²”“Adjusted R² (校正决定系数)”“AIC (赤池信息量准则)”“BIC (贝叶斯信息准则)”“RMSE (均方根误差)”和“模型整体检验”。

3个模型中复相关系数R、决定系数R²和校正R²随着变量的增加而逐渐变大，AIC、BIC、RMSE均随着变量的增加而逐渐变小，表明随着变量的加入模型对因变量的解释能力增加。模型3的决定系数R²为0.856，校正R²为0.844，AIC为128.601，BIC为140.074，RMSE为0.777，表明模型整体拟合较好。“模型整体检验”考察模型的整体显著性，可见3个模型均有统计学意义，表示3个模型中均至少有1个自变量具有统计学意义。

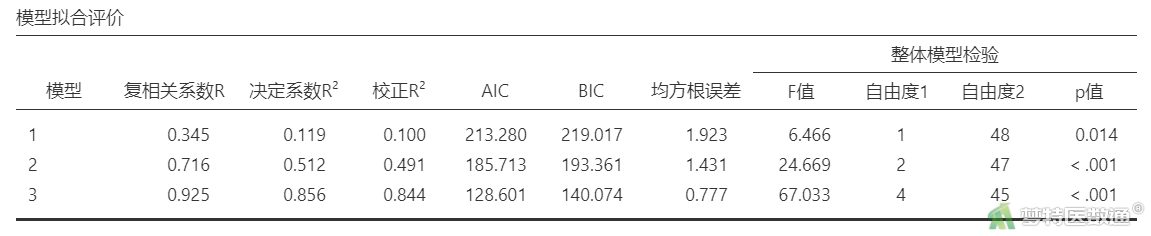
决定系数R²是回归平方和与总平方和的比值，它反应了回归方程对因变量的解释能力。但往往在多重线性回归方程中，自变量个数的增加会引起余差平方和的减少，使得R²增大，因此为了剔除自变量的个数对R²的影响，引入校正R²；一般情况下，自变量个数与样本量的比值大于1:5时，宜用校正R²来说明方程的拟合优度。

(2) 模型系数

“模型对比”(表9)和“Omnibus方差检验”(表10)可见，模型3中所有自变量均有统计学意义。

“模型系数 – 空腹血糖”表格(表11)列出了各自变量拟合后在模型3中的“系数(非标准化回归系数)”及其95%CI (置信区间)、SE (标准误)、t (统计量)、P (P值)、标准化系数及其95%CI。

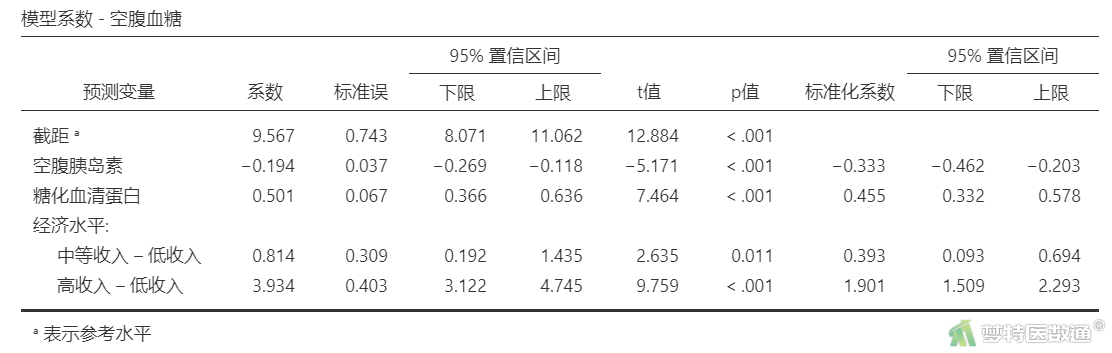
回归模型的截距为9.567，表示自变量取值为0时，因变量的取值，并无实际专业意义。变量“空腹胰岛素”的非标准化系数(即斜率)为-0.194 (95%CI -0.269~-0.118，P<0.001)，表示“空腹胰岛素”每增加1 mmol/L，空腹血糖减少0.194 mmol/L；变量“糖化血清蛋白”的非标准化系数(即斜率)为0.501 (95%CI 0.366~0.636，P<0.001)，表示“糖化血清蛋白”每增加1%，空腹血糖增加0.501 mmol/L。相比“低收入”人群而言，“中等收入”人群的非标准化系数为0.814 (95%CI 0.192~1.435，P=0.011)，表示“中等收入”人群比“低收入”人群空腹血糖高0.814 mmol/L；相比“低收入”人群而言，“高收入”人群的非标准化系数为3.934 (95%CI 3.122~4.745，P<0.001)，表示“高收入”人群比“低收入”人群空腹血糖高3.934 mmol/L。

据此可以写出本案例的回归方程为：

空腹血糖 = 9.567 - 0.194×空腹胰岛素 + 0.501×糖化血清蛋白+ 0.814×(经济水平=中等收入) + 3.934×(经济水平=高收入)

根据此方程输入相关自变量数值即可对空腹血糖进行预测。

四、结论

本研究采用多重线性回归模型考察“空腹血糖”是否受到性别、经济水平、空腹胰岛素和糖化血清蛋白的影响。通过绘制散点图，提示空腹胰岛素和糖化血清蛋白与空腹血糖之间存在线性关系，通过专业判断和Durbin-Watson检验提示数据之前相互独立，通过Cook's距离分析，提示数据不存在需要删除的异常值；通过VIF和容忍度判断自变量之间不存在严重多重共线性，通过Shapiro-wilk检验及绘制残差Q-Q图，提示残差符合正态分布；通过绘制残差图，提示残差方差齐。满足多重线性回归分析条件。

多元线性回归分析结果解读为，在其他变量不变的情况下，“空腹胰岛素”每增加1 mmol/L，空腹血糖减少0.194 mmol/L (β=-0.194，95%CI -0.269~-0.118；P<0.001)；“糖化血清蛋白”每增加1%，空腹血糖增加0.501 mmol/L (β=0.501，95%CI 0.366~0.636；P<0.001)；“中等收入”人群比“低收入”人群空腹血糖高0.814 mmol/L (β=0.814，95%CI 0.192~1.435；P=0.011)；“高收入”人群比“低收入”人群空腹血糖高3.934 mmol/L(β=3.934，95%CI 3.122~4.745，P<0.001)。

线性回归分析方程为：空腹血糖 = 9.567 - 0.194×空腹胰岛素 + 0.501×糖化血清蛋白+ 0.814×(经济水平=中等收入) + 3.934×(经济水平=高收入)。回归模型具有统计学意义，F=67.033，P<0.001；模型可以解释84.4%的因变量的变异(adjusted R²=0.844)。