配对卡方检验(Paired χ² Test)——R软件实现

关键词：R语言; R软件; 配对四格表; 配对卡方检验; McNemar检验

一、案例介绍

某实验室分别用A方法和B方法对600名患者血清中某抗体进行测定，其中1为阳性，2为阴性。问两种方法的检测结果有无差别？部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是比较两种方法的检测结果有无差别，属于配对设计，可以认为是在比较两种方法检测结果的一致性，或者比较两者阳性检测率的差异。每个数字代表的是一个对子，而不是单独的一个频数。对于本案例可采用2×2配对χ²检验(McNemar test)进行分析。但需要满足3个条件：

条件1：观察变量为二分类变量，本案例数据为检测方法的阴性和阳性，满足该条件。

条件2：试验方法或干预措施为两个，本案例为A和B两种检测方法，满足该条件。

条件3：研究设计为配对设计，即对同一批样本或研究对象进行两种方法的检测或干预。本案例对同一组患者使用两种抗体检测方法，为配对设计，满足该条件。

三、软件操作及结果解读

(一) 导入数据

mydata <- read.csv("配对卡方检验.csv")  #导入CSV数据
View(mydata)  #查看数据

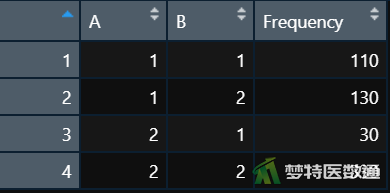
在数据栏目中可以查看全部数据情况，数据集中共有3个变量和4行观察数据，3个变量分别代表被A方法和B方法检测的结果频数(Frequency)。

如果数据集较大也可使用如下命令查看数据框结构：

str(mydata)  #查看数据框结构

(二) 适用条件判断

根据研究设计，本案例数据满足条件1—条件3。

(三) 统计描述及推断

1. 数据整理

(1) 软件操作

## 数据整理 ##
compare<-matrix(c(110,30,130,330),nr=2,dimnames = list(c("IFA-Positive", "IFA-Negative"), c("RPLA-Positive", "RPLA-Negative")))  #数据整理并编辑为矩阵格式
compare  #查看数据

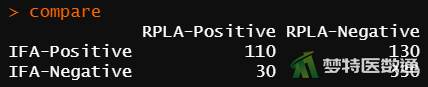
(2) 结果解读

图3的数据整理结果列出了卡方检验所需要的数据格式，并存储在“compare”数据框中。

2. 统计推断

(1) 软件操作

## 配对卡方检验  ##
mcnemar.test(compare, correct = FALSE)  #不进行连续性校正

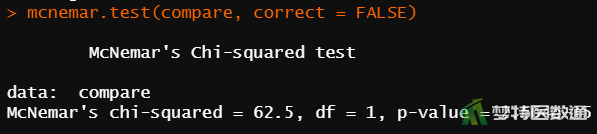
(2) 结果解读

图3中给出了A方法和B方法检测一致性的对子数和不一致的对子数，各自检测的阳/阴性频数。可知两种检测方法一致的有440对(同为阳性110对，同为阴性330对)，不一致的有160对(A方法为阳性，B方法为阴性130对；A方法阴性，B方法阳性30对)。

对于2×2配对四格表，定义四个格子分别为a、b、c和d，a、d为结果一致的频数，b和c为结果不一致的频数。需要根据b+c的大小，选择分析方法：当b+c≥40时，选择McNemar检验(2×2配对χ²检验)；当20≤b+c<40时，选择校正McNemar检验(Stata无法实现连续校正)；当b+c<20时，选择确切概率法。由于本案例b+c=160≥40，所以使用配对χ²检验的结果。

图4中mcnemar.test运行结果给出了配对χ²检验的统计量、自由度和P值。由于本案例b+c=160≥40，可以使用非校正检验。可知，\(x^2=62.5\)，P<0.001，提示两种方法检出的阳性率差异有统计学意义，即两种检测方法结果不同。

四、结论

本研究采用2×2 配对χ²检验(Paired Samples McNemar Tests)评价A方法和B方法检测患者血清中某抗体阳性率的一致性。结果显示检测不一致的有160对(A方法为阳性，B方法为阴性130对；A方法阴性，B方法阳性30对)；配对χ²检验分析发现，两种检测方法结果不同(\(x^2=62.5\)，P<0.001)。