配对卡方检验(Paired χ² Test)——理论介绍

关键词：配对四格表; 配对卡方检验; McNemar检验

一、适用条件

条件1：分类变量或观察变量为二分类变量。

条件2：试验方法或干预措施为两个。

条件3：研究设计为配对设计，即对同一批样本或研究对象进行两种方法的检测或干预。

二、统计量计算

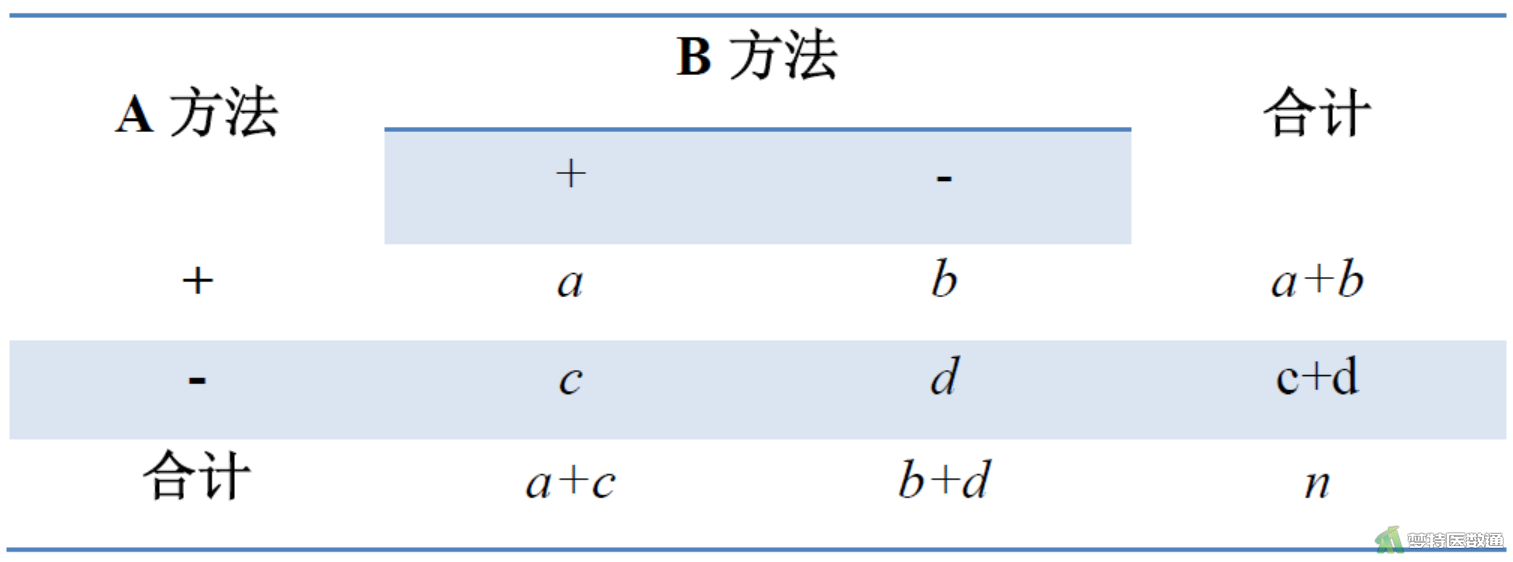
以图1为例，使用A、B两种方法检测某种指标，试问两种方法的检测结果有无差别。图中两种检测方法皆为阳性的数量为a，两种检测方法皆为阴性的数量为d，A方法结果为阳性、B方法为阴性的数量为b，A方法结果为阴性、B方法为阳性的数量为c。其中a、d为观察结果一致的两种情况，b、c为观察结果不一致的两种情况。当两总体率相等，即π₁＝π₂时则有B=C。由于在抽样研究中，抽样误差是不可避免的，样本中的b和c往往不等(即两样本率不等：p₁≠p₂)。为此，需进行McNemar假设检验，其检验统计量根据b＋c的总例数分为

校正公式为：

需要注意的是，该方法一般用于样本含量不太大的资料，因为该法仅考虑了两种检测方法结果不一致的两种情况(b和c)，而未考虑样本含量n和两种方法结果一致的两种情况(a和d)。所以，当n很大且a与d的数值很大(即两法的一致率较高)，b和c的数值相对较小时，即便是检测结果有统计学意义，其实际意义往往也不大。

三、案例数据

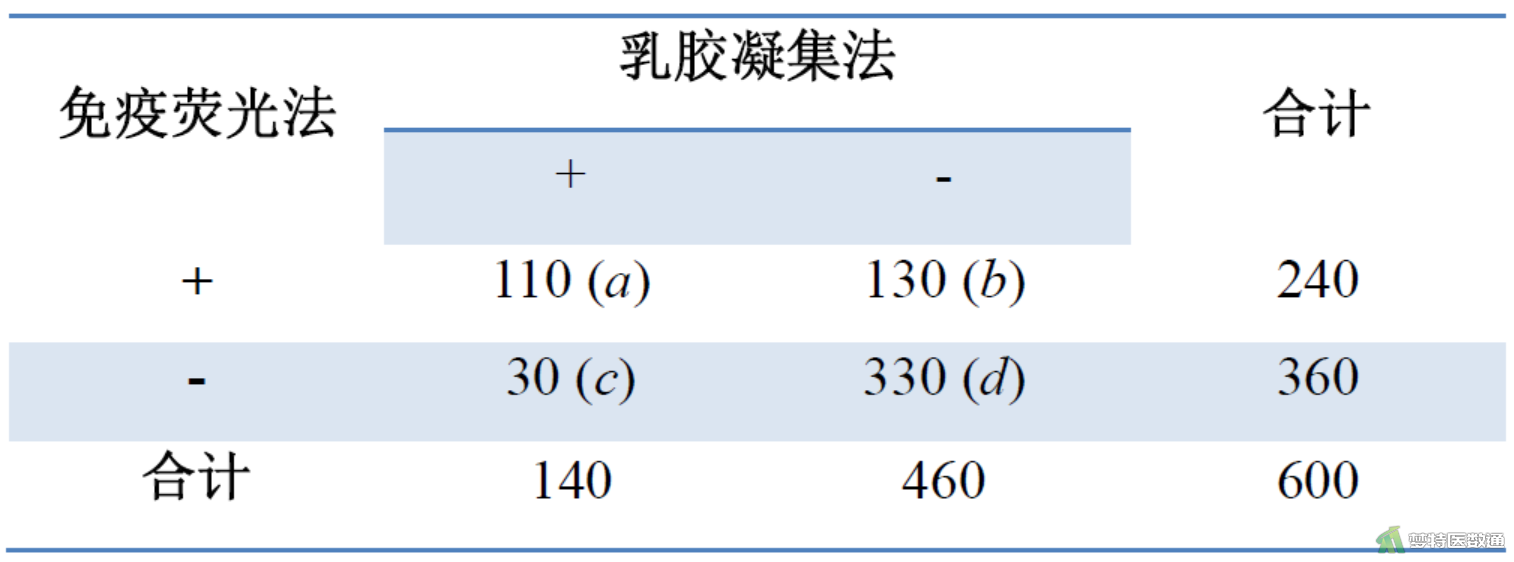
某实验室分别用乳胶凝集法(RPLA)和免疫荧光法(IFA)对600名患者血清中某抗体进行测定，数据见图1。问两种方法的检测结果有无差别？

四、假设检验

(一) 建立检验假设，确定检验水准

H₀：B=C，即两种方法的检测结果相同

H₁：B≠C，即两种方法的检测结果不相同

α=0.05.

(二) 计算检验统计量

b+c=160，＞40，故用非校正公式计算得

\(\chi^2=\frac{(b-c)^2}{b+c}=\frac{(130-30)^2}{130+30}=62.5\)

(三) 确定P值，作出推断结论

自由度v=1，查(χ²界值表),得\(\chi_{0.05,1}^2\)=7.88。本例χ²=62.5＞\(\chi_{0.05,1}^2\)，故P＜0.05。在α=0.05检验水准拒绝H₀，接受H₁，可认为两种方法的检测结果不同。

再计算两种方法阳性结果的检出率，可知：

免疫荧光法的检验阳性率\(p_{1}=\frac{110+130}{600} \times 100 \%=40 \%\)

乳胶凝集法的检验阳性率\(p_{2}=\frac{110+30}{600} \times 100 \%=23.33 \%\)

因此，两种方法的阳性检出率从专业比较也存在较大的差异，综合配对χ²检验的结论，可认为两种方法的检测结果不同。