χ²检验(chi-square test)是以χ²分布为理论依据,用途颇广的假设检验方法,包括推断两个或多个总体率或构成比之间有无差别、多个样本率或构成比间的多重比较、两个分类变量之间有无关联性和频数分布拟合优度的χ²检验。本篇文章将介绍四格表资料的χ²检验的适用条件及检验假设。
关键词:卡方检验; 理论频数; 实际频数; 四格表
一、四格表资料的χ²检验适用条件
条件1:分组变量与观察变量均为二分类变量。
条件2:观察变量相互独立。
条件3:总例数≥40,且所有期望频数(理论频数)≥5。
二、四格表资料的χ²检验统计量计算
(一) 专用公式
四格表资料χ²检验的专用公式为
χ² =\(\frac{(a d-b c)^{2} n}{(a+b)(c+d)(a+c)(b+d)} \)
式中a、b、c、d为四格表的实际频数;(a+b)、(c+d)、(a+c)、(b+d)是周边合计数;a+b+c+d= n为总例数。上述专用公式是将各符号带入理论频数T的计算公式和χ²值的基本公式(查看公式)计算所得,省去了计算理论频数的步骤,简化了计算。
(二) 矫正公式
计数资料中的实际频数A为分类资料,是不连续的,按χ²值的基本公式计算的χ²值是离散型分布。(χ²界值表)的依据是χ²分布,而χ²分布是连续型分布。因此,按χ²值的基本公式计算的χ²值查(χ²界值表)所得的概率P偏小,特别是当自由度ν为1的四格表资料。为此,美国统计学家F·Yates于1934年提出了|A-T|-0.5计算χ²值的连续性校正公式:
\( \chi_{c}^{2}=\sum \frac{(|A-T|-0.5)^{2}}{T} \) ,
\( \chi_{c}^{2}=\frac{\left(|a d-b c|-\frac{n}{2}\right)^{2} n}{(a+b)(c+d)(a+c)(b+d)} \)上述两个公式分别是基本公式和专用公式的校正形式。
在实际工作中,对于四格表资料,通常规定为:
(1) 当n≥40且所有的T≥5时,用χ²检验的基本公式或四格表资料χ²检验的专用公式;当P≈α时,改用四格表资料的Fisher确切概率法。
(2) 当n≥40且有1≤T<5时,用四格表资料χ²检验的校正公式;或改用四格表资料的Fisher确切概率法。
(3) 当n<40,或T<1时,用四格表资料的Fisher确切概率法。
三、案例数据
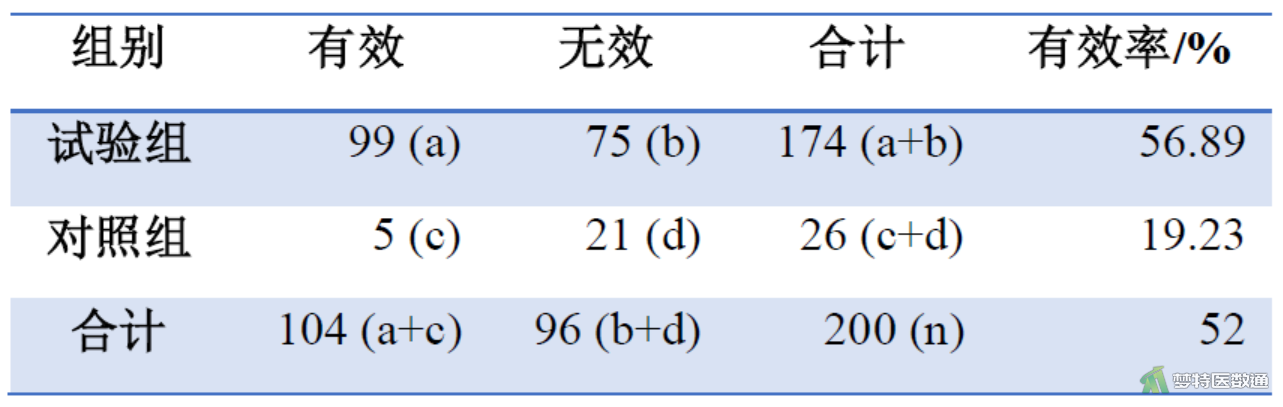
某中医院欲比较某经典名方控制高血压的效果。将200例高血压患者随机分到试验组(Trial group)和对照组(Control group),随访三个月后患者的血压控制情况[分为有效(Effective)和无效(Noneffective)]。问该经典名方控制血压的效果如何?数据见图1。
四、四格表资料的χ²检验步骤
以上例进行说明。本案例的分组变量(组别)和观察变量(疗效)均为二分类变量,且本研究中各研究对象的观察变量都是独立的,不存在互相干扰的情况。可尝试使用χ²检验进行分析。。
(一) 建立检验假设,确定检验水准
H0:π1=π2,试验组和对照组的总体血压控制率相等
H1:π1≠π2,试验组和对照组的总体血压控制率不相等
α=0.05
(二) 计算检验统计量
1. 计算理论频数T
由上文可得,本例n≥40,因此需要计算理论频数T,判断选择何种公式。
按理论频数T的计算公式计算T11、T12、T21、T22:
\( T_{11}=\frac{174 \times 104}{200}=90.48, \quad T_{12}=\frac{174 \times 96}{200}=83.52 \) \( T_{21}=\frac{26 \times 104}{200}=13.52, \quad T_{22}=\frac{26 \times 96}{200}=12.48 \)可知所有的T≥5,可以用基本公式或四格表资料χ²检验的专用公式计算χ²值。
2. 计算χ²值
按基本公式计算χ²值:
\( \frac{(99-90.48)^{2}}{90.48}+\frac{(75-83.52)^{2}}{83.52}+\frac{(5-13.52)^{2}}{13.52}+\frac{(21-12.48)^{2}}{12.48}=12.857 \)或按四格表资料χ²检验的专用公式计算χ²值:
\( \frac{(a d-b c)^{2} n}{(a+b)(c+d)(a+c)(b+d)}=\frac{(99 \times 21-75 \times 5)^{2} \times 200}{174 \times 26 \times 104 \times 96}=12.857 \)按自由度计算公式计算ν:ν=(2-1)(2-1)=1
(三) 确定P值,作出推断结论
按ν=1,α=0.05,查(χ²界值表),得 \( \chi_{0.05,1}^{2} \) =3.84。本例\(\chi^{2} > \chi_{0.05,1}^{2} \) ,故P<0.05。在α=0.05水平上拒绝H0,接受H1,可认为两组高血压患者的血压控制率的差异有统计学意义。