在前面文章中我们分别介绍了2×2 Fisher确切概率法的假设检验理论,本篇文章将使用案例演示在R软件中实现2×2 Fisher确切概率法的操作步骤。
关键词:R语言; R软件; 卡方检验; Fisher确切概率法; Fisher精确检验; 费希尔确切概率法; 费希尔精确检验
一、案例介绍
某医师为研究术前使用抗菌药A预防术后感染的效果,将34例行人工全膝关节置换术的患者随机分为试验组(Trial group,用“1”表示)和对照组(Control group,用“2”表示),收集患者术后感染的情况[分为阳性(Positive,用“1”表示)和阴性(Negative,用“2”表示)],问两组患者术后感染率有无差别?部分数据见图1。本文案例可从“附件下载”处下载。
二、问题分析
本案例的分析目的是比较两组患者术后的感染率有无差异,由于总例数(34例)<40,因此需要考虑使用Fisher确切概率法。但需要满足2个条件:
条件1:分组变量和观察变量均为二分类变量,本案例数据满足该条件。
条件2:观测值相互独立,本案例数据满足该条件,研究对象的术后感染情况互不干扰。
本案例数据采用了频数资料录入方法,设置分组变量、观察变量及频数变量,该形式在进行χ2检验时较为常见,进行统计分析前需要进行数据的重新整理,形成可分析的矩阵格式。此外,数据还有一种非频数资料录入方式,只有分组变量和观察变量两列,每一行为一个患者的数据,该形式是在R软件中进行各种统计分析最常用的资料形式,进行检验前不需要进行数据的重新整理。
三、软件操作及结果解读
(一) 导入数据
mydata <- read.csv("2×2 Fisher确切概率法.csv") #导入CSV数据
View(mydata) #查看数据
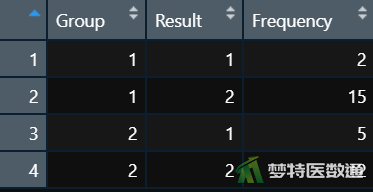
在数据栏目中可以查看全部数据情况,数据集中共有3个变量和4行观察数据,3个变量分别代表被调查者的分组(Group)、术后感染情况(Result)及频率(Frequency)。
如果数据集较大也可使用如下命令查看数据框结构:
str(mydata) #查看数据框结构
(二) 适用条件判断
本案例的数据满足上述条件。
(三) 统计描述及推断
1. 数据整理
(1) 软件操作
## 数据整理 ##
compare<-matrix(c(2,5,15,12),nr=2,dimnames = list(c("Trial group","Control group"),c("Effective","Noneffective"))) #数据整理并编辑为矩阵格式
compare #查看数据

(2) 结果解读
图3的数据整理结果列出了Fisher确切概率法所需要的数据格式,并存储在“compare”数据框中。
2. 统计推断
(1) 软件操作
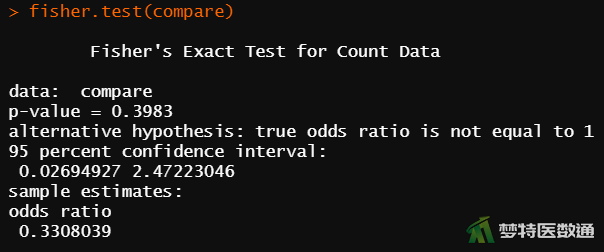
fisher.test(compare) #Fisher确切概率法
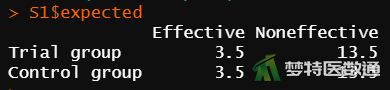
## 查看期望频数 ## S1<-chisq.test(compare,correct = FALSE) #不进行连续性校正 S1$expected #查看期望频数
(2) 结果解读
图4“Fisher.test”(Fisher确切概率法)给出了Fisher确切概率法的P值,由P=0.3983可知按照α=0.05的检验水准,两组患者术后感染率的差异无统计学意义,尚不能认为试验组和对照组的术后感染率不同。图5给出了试验组(Trial group)、对照组(Control group)的期望频数。
3. 计算构成比
(1) 软件操作
S2<-prop.table(compare,margin = 1) #计算行百分比 S2 #显示行百分比
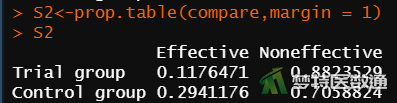
(2) 结果解读
图6给出了试验组 (Trial group)和对照组(Control group)感染者的行百分比,可知试验组和对照组的术后感染率分别为11.8%和29.4%。
四、结论
本研究采用2×2 Fisher确切概率法对两组患者术后感染率进行比较分析,由于总例数(34例)<40,应使用Fisher确切概率法进行分析。分析结果显示,试验组患者的术后感染率为11.8%,对照组的术后感染率为29.4%,Fisher确切概率法的P值为0.398>0.05,提示两组患者的术后感染率的差异无统计学意义,尚不能认为两组患者的术后感染率不同。