Friedman检验(The Friedman Non-parametric Repeated Measures ANOVA Test)——Stata软件实现

关键词：Stata; 非参数检验; 秩和检验; Friedman检验; 重复测量非参数检验

一、案例介绍

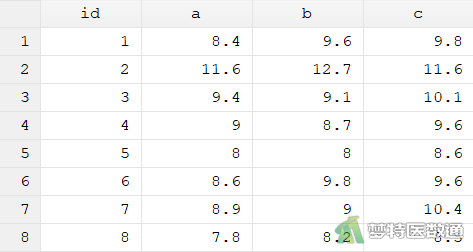
8名受试对象在相同试验条件下分别接受A、B、C 3种不同频率振动的刺激，测量其反应率(%)，问3种频率振动刺激的反应率是否有差别？部分数据见图1。本文案例可从“附件下载”处下载。

二、问题分析

本案例的分析目的是判断多组相关数据的差异，首先对三组数据进行正态性检验，若发现不符合正态分布，可以使用Friedman检验(此处的“反应率”是针对个体观察对象所测得的一个反应程度的指标，可以理解为“反应指数”，因此属于连续变量)。Friedman检验可应用于多组配对或相关数据的秩转换非参数检验，但需要满足两个条件：

条件1：观察变量为连续变量或有序分类变量。本研究中反应率为连续变量，该条件满足。

条件2：观察变量具有3个及以上的分组，为配对设计，或各组之间存在相关性。本研究中3组数据均是对同一批研究对象所测量，该条件满足。

三、软件操作及结果解读

(一) 适用条件判断

1. 软件操作

①*使用Shapiro-Wilk检验分别考察每组的数据的正态性*

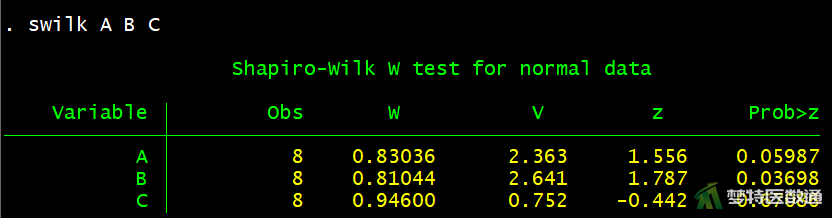
swilk A B C

②*绘制每组数据的正态分位图*

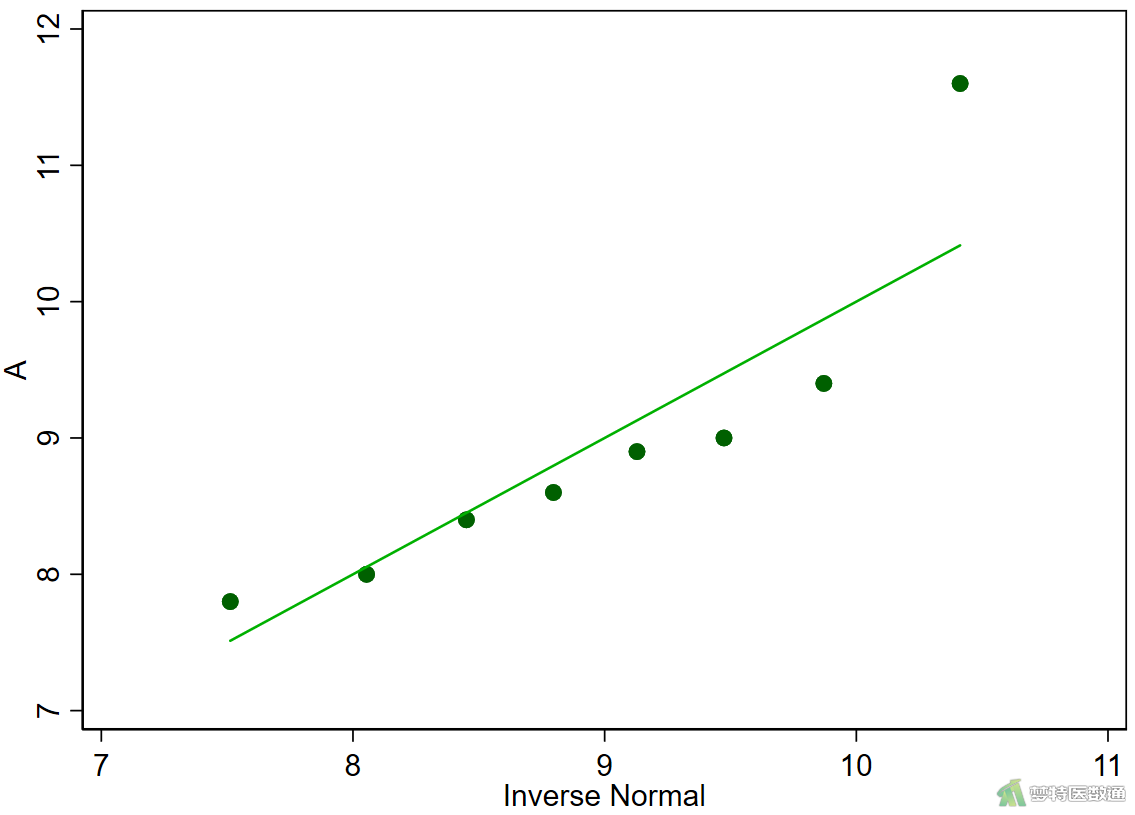
qnorm A

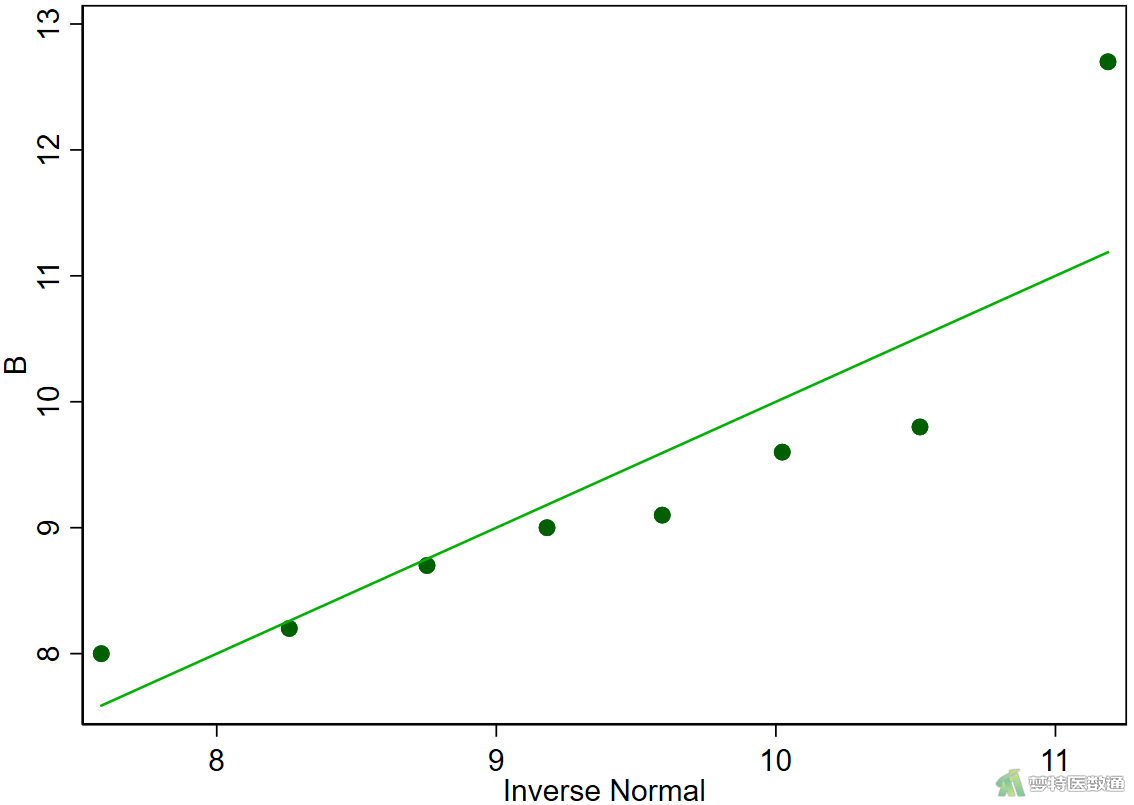
qnorm B

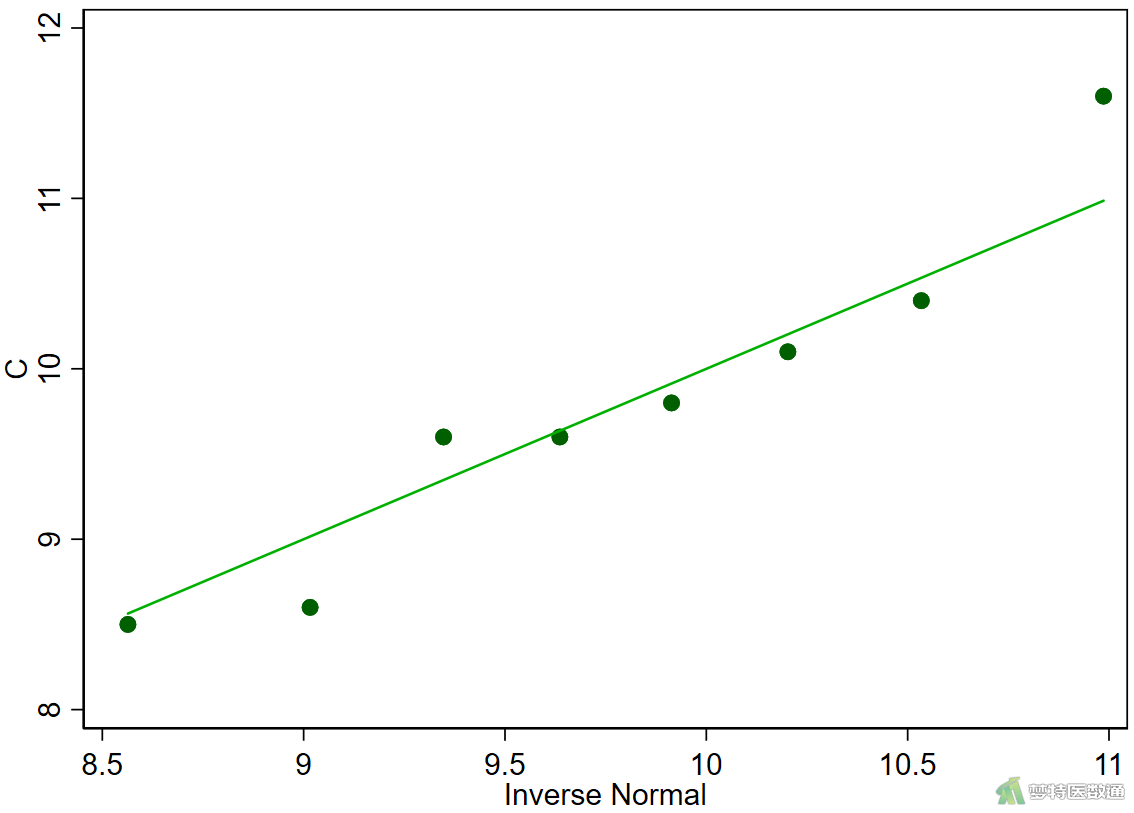
qnorm C

2. 结果解读

由图2的正态性检验结果“Shapiro-Wilk W”显示A、B、C三组的P=0.060、0.037、0.671，前两组P值均<0.1，提示两组数据不服从正态分布。从图3—图5的正态分位图上可见，三组数据散点偏离对角线较远，尤其是A、B两组数据，也提示数据不服从正态分布。因此，本案例应使用Friedman检验比较三组反应率的差异。关于正态性检验的注意事项详见文章(医学统计学核心概念及重要假设检验的软件实现(2/4)——正态性假设检验的SPSS实现)。

(二) 统计描述及推断

1. 统计描述

(1) 软件操作

*描述性分析*

tabstat A B C, stat(count mean sd var q)

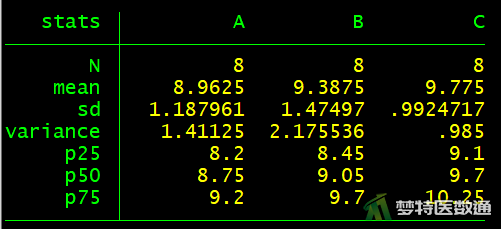
(2) 结果解读

图6“tabstat(统计描述)”提供了研究案例的“N(样本量)”、“Mean(均数)”、“sd(标准差)”、“p25(第1四分位数)”、“p50(中位数)”和“p75th(第3四分位数)”。可知，受试者对A频率振动的反应率为8.75% (P₂₅~P₇₅：8.2%~9.2%)；对B频率振动的反应率为9.05% (P₂₅~P₇₅：8.45%~9.7%)；对C频率振动的反应率为9.7% (P₂₅~P₇₅：9.1%~10.25%)。

2. 统计推断

(1) 软件操作

①安装friedman模块

help friedman

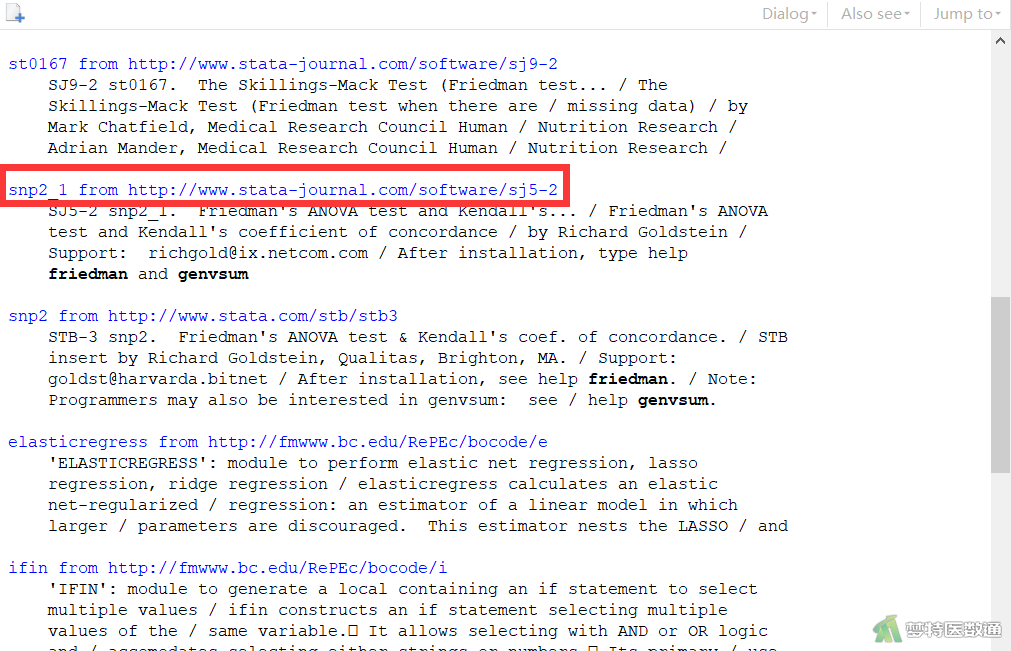
在图7页面中点击红色框内链接。

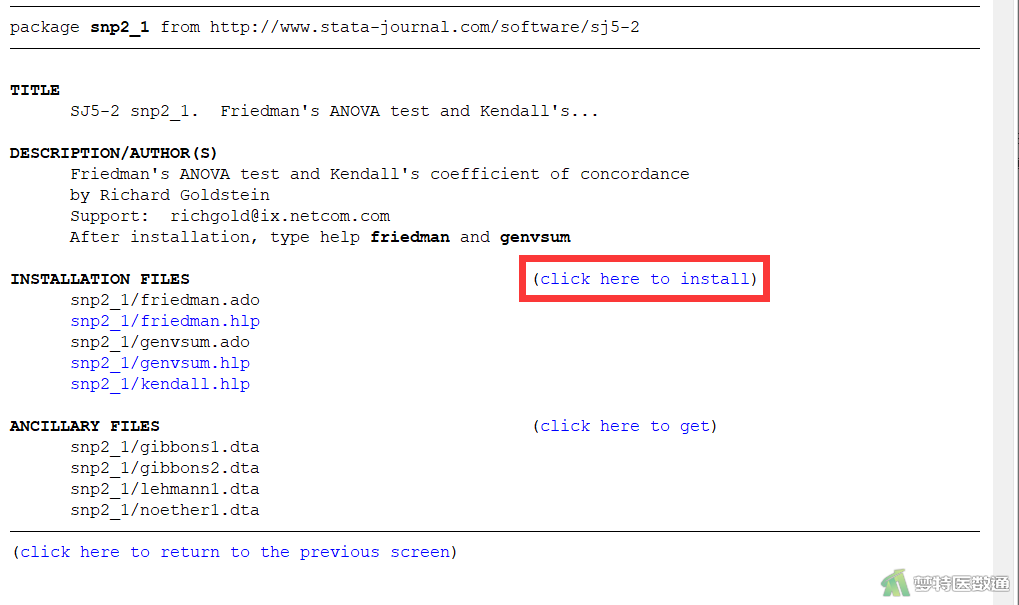
在图8页面中点击“click here to install”。

②*Friedman检验*

friedman A B C

(2) 结果解读

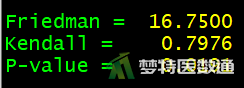
图9显示了Friedman检验的结果。由“Friedman”结果可知，Friedman值= 16.7500, P = 0.0191，差异有统计学意义。即3种频率振动刺激的反应率总体比较差别具有统计学意义(P<0.05)。

 四、结论

本案例欲比较在A、B、C 3种不同频率振动的刺激下受试者的反应率(%)是否存在差异。通过绘制正态分位图和Shapiro-Wilk检验，提示数据不服从正态分布，故采用Friedman检验对数据进行分析。

结果显示，受试者对A、B、C 3种不同频率振动的刺激反应率(%)分别为8.75% (P₂₅~P₇₅：8.2%~9.2%)；9.05% (P₂₅~P₇₅：8.45%~9.7%)；9.7% (P₂₅~P₇₅：9.1%~10.25%)，差异有统计学意义(Friedman值= 16.7500, P = 0.0191)。