当因变量为二分类变量(如是否发生某病,死亡和存活等)时,可以采用二分类logistic回归和条件logistic回归进行影响因素分析;当因变量为有序多分类变量(等级变量)时,例如疾病的严重程度(轻/中/重),可以采用有序logistic回归(Ordinal Logistic Regression)进行分析。本篇文章将举例介绍有序logistic回归的假设检验理论。
关键词:有序logistic回归; 有序逻辑回归; 平行性检验; 比例优势检验
一、基本概念
对于有序logistic回归,是根据有序多分类变量拆分成多个二分类因变量,拟合多个二分类logistic回归,并基于累积概率构建回归模型。假设因变量为疾病的严重程度:轻、中、重,分别赋值为1、2和3,那么因变量的拆分形式如下:1 vs 2+3、1+2 vs 3;若因变量为4个等级1、2、3、4,那么则有1 vs 2+3+4、1+2 vs 3+4、1+2+3 vs 4。这里就需要满足比例优势假设,即在拆分的多个二分类logistic回归中,除了截距不同,自变量对应的模型系数均相等。也就是假定自变量在多个模型中对累积概率的优势比影响相同。不同类别累积概率的差别体现在常数项上。若以i代表因变量的第i分类,那么该模型的公式可如下表示:
\(\begin{aligned}\operatorname{logit}[P(Y \leq&\mathrm{i} \mid\mathrm{X})]=\ln \left[\frac{P(Y \leq i \mid X)}{1-P(Y\leq i \mid X)}\right] \\=& \beta_{0 i}+\beta_{1} X_{1}+\beta_{2}X_{2}+\cdots+\beta_{m} X_{m}\end{aligned}\)
可知,Y取1时的概率为:
\(P_{1}=P(Y \leq 1 \mid X)=\frac{1}{1+\exp\left[-\left(\beta_{01}+\beta_{1} X_{1}+\beta_{2}X_{2}+\cdots+\beta_{m} X_{m}\right)\right]}\)
那么,Y取i时的概率为:
\(\begin{aligned}P_{i}=P(Y \leq&i \mid X)-P(Y \leq i-1 \mid X) \\&=\frac{1}{1+\exp \left[-\left(\beta_{0 i}+\beta_{1}X_{1}+\beta_{2} X_{2}+\cdots+\beta_{m}X_{m}\right)\right]} \\&-\frac{1}{1+\exp \left[-\left(\beta_{0 i-1}+\beta_{1}X_{1}+\beta_{2} X_{2}+\cdots+\beta_{m}X_{m}\right)\right]}\end{aligned}\)
二、适用条件
有序多分类logistic回归需要满足5个条件:
条件1:因变量唯一,且为有序多分类变量。
条件2:存在一个或多个自变量。可为定性与定量变量。
条件3:因变量的观察结果相互独立。
条件4:自变量之间无多重共线性。
条件5:满足平行性检验(即比例优势假设)。
三、参数估计
变量回归系数的估计与二分类logistic回归的类似,详见(https://mengte.online/archives/3693)。
四、假设检验
模型和变量回归系数的假设检验与二分类logistic回归的类似,详见(https://mengte.online/archives/3693)。
五、案例分析
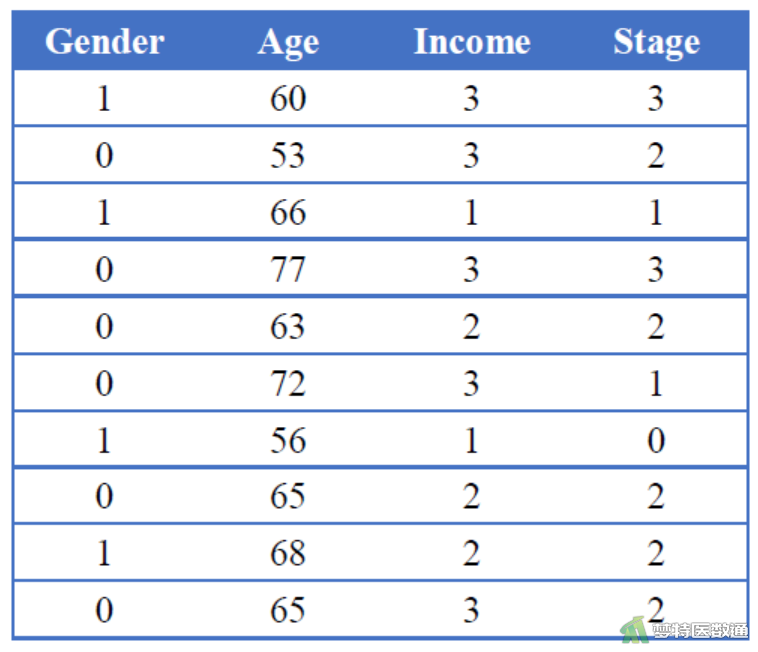
在某胃癌筛查项目中,为了确定胃癌筛查的重点人群,研究者想了解首诊胃癌分期(Stage) (0=I-II期、1=III期、2=IV期、3=V期与患者经济水平(Income) (1=低水平、2=中等水平、3=高水平)、性别(Gender) (1=女性、0=男性)和年龄(Age)之间的关系,试对数据进行分析。部分数据见图1。
对该资料拟合有序logistic回归。通过软件分析可得到每个自变量对应的χ2值,截距、每个自变量的哑变量对应的回归系数。
(一) 模型整体检验
对该模型进行整体假设检验,步骤如下:
1. 建立假设检验,确定检验水准
H0:β1=β2=β3=0;
H1:βi (i=1、2、3)不全为0。
α=0.05
2. 计算检验统计量
通过软件可得到有序logistic回归模型的似然比统计量为χ2=35.988。
3. 确定P值,做出统计推断
统计量服从自由度为4的χ2分布。由此可确定,P<0.001,即模型整体有统计学意义,说明模型中至少存在一个自变量有统计学意义。
(二) 模型系数检验
对每个自变量的回归系数进行检验,即判断每个自变量对模型是否有贡献。常用的假设检验为Wald检验。
1. 建立假设检验,确定检验水准
H0:βi=0;
H1:βi≠0。
α=0.05
2. 计算检验统计量
通过软件分析可得到统计量Wald χ2值。
3. 确定P值,做出统计推断
图2“Omnibus似然比检验)”中列出了每个自变量在模型中是否有统计学意义,可知年龄(χ2=17.003,P<0.001)、收入(χ2=12.663,P=0.002)在模型中有统计学意义,性别(χ2=0.697,P=0.404)在模型中无统计学意义。
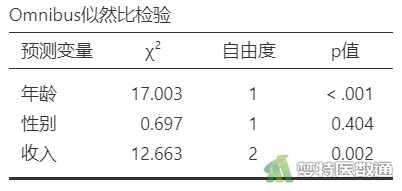
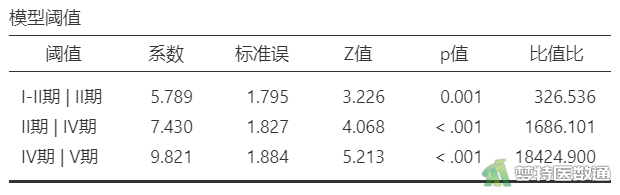
图3列出了各自变量拟合后的回归系数及其95%CI、标准误、Z统计量、P值、“比值比(OR值)”及其95%CI。其中“年龄”的P<0.001,有统计学意义;OR=1.118 (95%CI:1.060~1.180),表示年龄每增加一岁,其首诊“胃癌分期”提升一个等级的可能性是原来的1.118倍。“中等收入”水平患者首诊“胃癌分期”提升一个等级的可能性是“低收入”水平患者的3.290倍(95%CI:1.689~6.503,P<0.001);“高收入”水平患者首诊“胃癌分期”提升一个等级的可能性是“低收入”水平患者的2.396倍(95%CI:1.188~4.885,P=0.015)。

图4列出了各个模型的常数项,由于因变量有4个水平,共生成4-1=3个模型。